算法专题——双连通分量

概念

也叫重连通分量.由于无向图的连通更加容易, 所以比起有向图中连通更加注重节点之间能否相互到达的特点, 无向图的连通会更加注重块与块之间能否相互到达.于是也会更加注意一个连通块中, 一些边和点对于整个连通块的影响.双连通分量分为两类.

边双连通分量, 对应的会影响分量的连通性的边称为割边, 也叫桥. 为极大的不包含割边的连通块.
点双连通分量, 对应的会影响分量的连通性的点称为割点. 为极大的不包含割点的连通块

点双和边双并不会互通. 即一个分量是点双不一定是边双, 反之亦然.

与强连通分量相似, 找双连通分量通常也只是求解问题中的一个步骤, 缩点之后, 才是真正的开始.

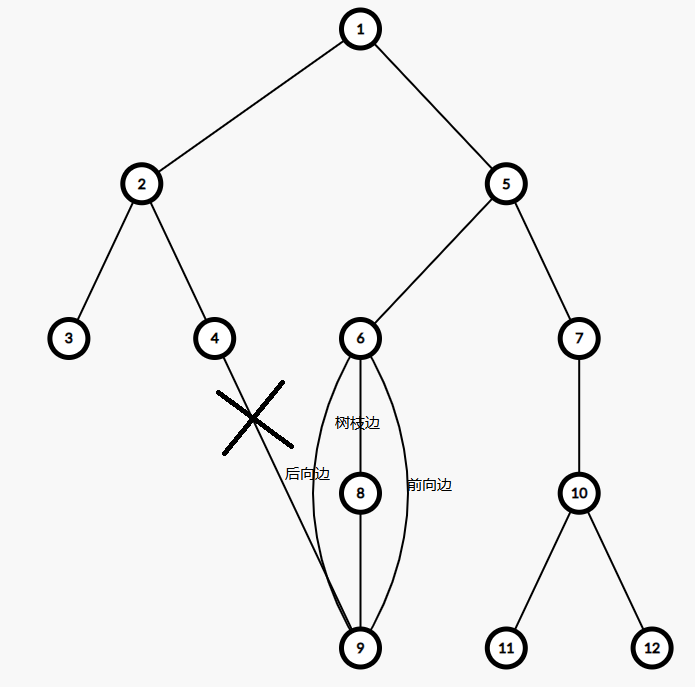
不同于有向图, 无向图没有横叉边, 至于具体原因, 可以自己想想.

边双的性质

边双图中任意两点之间至少存在两条边不重合的路径.(边双同有向图的强连通分量一样, 可以看作一个环的耦合连接)
非割边的边仅属于一个边双, 割边不属于任意一个边双.
边双缩点之后会得到一棵树.

点双的性质

除去一种特殊的点双外, 其他的点双图中任意两点之间至少存在两条点不重合的路径.
非割点的点仅属于一个点双, 割点至少属于一个点双.
点双缩点之后可以得到一颗具有二分图性质的树(割点不为叶节点).

找边双连通分量

边双连通分量的求解也可以使用Tarjan算法实现, 由于·横叉边已不存在, 因此对于以访问过的节点, 一定都仍然存储于dfs栈中(可以自己想想为啥, 和无向图没有横叉边的原因一致).

代码：

int dfn[MAXN], low[MAXN], timestamp, stk[MAXN], top;
int dcc_cnt, bridge, is_bridge[MAXN], id[MAXN], size[MAXN];
void Tarjan(int u, int pre) {
    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u;
    int v;
    for (int i = h[u]; ~i; i = ne[i]) {
        v = e[i];
        if (!dfn[v]) {
            Tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (dfn[u] < low[v]) {									//cal bridge
                bridge++;
                is_bridge[i] = is_bridge[i ^ 1] = true;
            }
        }
        else if (i != (pre ^ 1)) low[u] = min(low[u], dfn[v]);		//不为父节点
    }
    if (low[u] == dfn[u]) {
        dcc_cnt++;
        do {
            v = stk[top--];
            id[u] = dcc_cnt;										//coloring
            size[dcc_cnt]++;										//cal s
        } while (v != u);
    }
}

找点双连通分量

仍然是Tarjan算法, 但加了一些特判处理.

一个点是割点, 仅当其一个子节点不能到达该点的父节点（即dfn[u] <= low[v]）, 且该节点至少连接两个子树时成立.对于非根节点的节点而言, 可以到达该点必然是通过父节点一侧的子树过来的, 再连接一个子节点一侧的子树即可, 而对于根节点而言, 则需要进行一个特判, 判断其是否至少与两个子树相连.具体看代码.

一个点是不是割点需要进行以上的特判, 但一个点所连接的子树是不是点双, 则只要dfn[u] <= low[v]成立即可.具体看代码.

代码：

int dfn[MAXN], low[MAXN], timestamp;
int stk[MAXN], top;
int dcc_cnt, cut[MAXN];
vector<int> dcc[MAXN];

void Tarjan(int u) {
    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u;
    if (u == root && h[u] == -1) {		//一个点也是点双
        dcc_cnt++;
        dcc[dcc_cnt].push_back(u);
        return ;
    }
    int cnt = 0, v;						//记录
    for (int i = h[u]; ~i; i = ne[i]) {
        v = e[i];
        if (!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                cnt++;										//is a subtree
                if (u != root || cnt > 1) cut[u] = true;	//cutJudge
                dcc_cnt++;
                int y;
                do {
                    y = stk[top--];
                    dcc[dcc_cnt].push_back(y);
                } while (y != v);
                dcc[dcc_cnt].push_back(u);					//get dcc
            }
        }
        else low[u] = min(low[u], low[v]);					//no effect
    }
}

例题

Redundant Paths

题面：

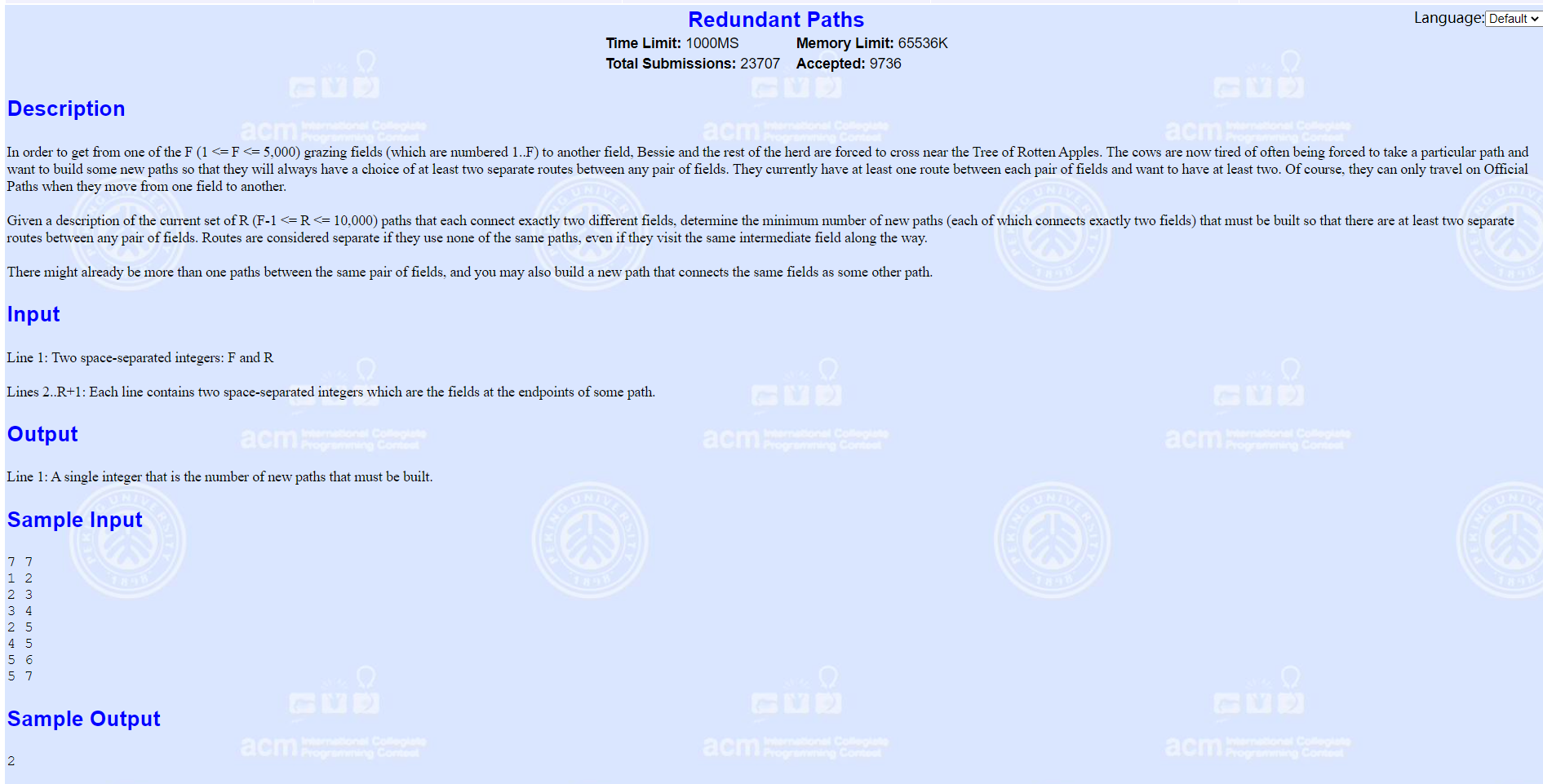
分析：

给出一个无向图, 求解需要添加多少条边可以将原图变成一个边双.

直接使用二级结论：缩点之后得到一颗树, 需要添加的边数即为(叶子节点数 + 1) / 2, 即边数的一半向上取整, 下面给出证明.

我们知道, 一个简单的边双就是一个一个环,一个复杂的边双就是多个环进行的耦合连接, 因此得到一颗树之后, 我们的任务就是要连接最少的边将原图连接成一个环. 而环的性质在于没有一个点的度为1, 所有点的度都大于1. 而对于一颗树而言, 其拥有叶子节点个数个度为1的点, 所以, 一种朴素的想法就是通过连接一条边, 减少树中的叶子节点, 减少度为1的点, 最为理想的情况连接两个叶子节点可以消去两个度为1的点, 但是在消去两个叶子节点的同时, 还要防止新的叶子节点生成(新的叶子节点只由缩点之后的得到的点产生), 因此选择哪两个叶子节点进行连接非常重要. 连接两个节点之后会进行缩点从而再进行下一步的连接, 缩点的对象是以两个叶子节点为端点的一条链, 缩点之后将其变为一个点, 而为了防止该点变成叶子节点, 选择的两个叶子节点对应的链上至少与其他两条链相连. 而在连接的过程中, 总是可以找到这样的两个叶子节点, 使其对应的链满足条件. 因此只需要连接(叶子节点数 + 1) / 2条边.

边界条件: 叶子树为1, 不需要加边; 叶子数为2, 加一条边; 叶子数为为3, 连接两条边. 代码略.

矿场搭建

题面:

分析:

给出一个图, 破坏图中任意一个点, 求至少需要设置多少个救援出口, 使得其他没有被破坏的点都可以到达救援出口. 询问点之间的到达性问题, 可以很自然的想到用到点连通分量, 当一个点被破坏时, 一个点双中的其他点总是可以到达点双中没有破坏的任意一点, 所以在一个独立的点双中仅需要设置两个出口即可, 显然与点双的关系十分密切. 对于更加深入的讨论, 我们可以将原图进行一个缩点得到一个树, 即询问在一颗特殊的树中需要至少设置多少个节点, 使得其满足题目的条件.

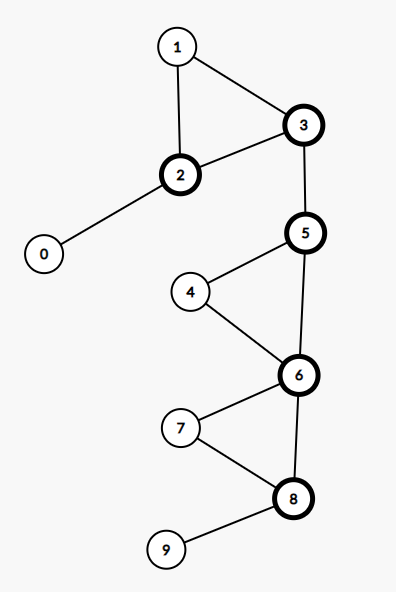
接下来讨论点双缩点后可以得到的图的特点, 从左边的原图得到右边缩点后的图, 可以发现该树的几个特点: 割点(黑色)一定不为叶子节点, 割点与点双总是交替出翔. 在这道题中, 我们可以发现割点起到了枢纽的作用, 如果割点被破坏, 那么要保证割点连接的几个点双内都有逃生出口. 下面先考虑割点被破坏的情况. 对于叶子节点, 由于仅与一个割点连接, 因此其割点被破坏的时候该点双内部应该也要有一个出口, 所以该树中的首先应该就要有叶子节点个数个出口, 而对于非叶子节点的点双而言, 其割点被破坏后, 不管被分到哪一个部分, 也总是存在一条路径可以到达叶子节点, 所以不需要在非叶子节点设置出口. 再考虑被破坏的不是割点的情况, 那么可以得到原图的连通性不会被破坏, 只要在该图中有任意两个出口即可.

综上可以得到, 对于一个点双树而言, 至少需要设置叶子节点个数个出口, 方案数是叶子节点的点数 - 1(割点不能设置), 同时注意一下边界条件, 即树中仅一个点双的情况.

核心代码:

for (root = 1; root <= n; root++) 
    if (!dfn[root]) Tarjan(root);

ull res = 0, sch = 1; 
for (int i = 1; i <= dcc_cnt; i++) {
    int cnt = 0, lim = dcc[i].size();
    for (int j = 0; j < lim; j++) {
        if (cut[dcc[i][j]]) cnt++;

    }
    if (cnt == 0) res += 2, sch *= (ull)dcc[i].size() * (dcc[i].size() - 1) / 2;
    else if (cnt == 1) res++, sch *= dcc[i].size() - 1;
}
printf("Case %d: %llu %llu\n", ++ca, res, sch);

TanJI_C

Github：github.com/TanJI-C