算法专题——并查集
并查集的特点
故名思意,并 + 查 + 集合 == 并查集,即有合并与查询两种操作的集合(不如说是一种图),至于更基础的概念可以看其他的博客。并查集主要用来处理分组问题,例如已经给出了几个节点之间的连接结果(1与3相连,3与4相连),询问某两个节点之间是否存在连通关系(1与4死否连通),或者询问有几个组(134,2共两个)。而更加复杂的并查集则涉及到拓展域,边权的问题,不过本质还是讨论连接的问题,例如最普通的并查集可以处理是A与B相连的情况,而拓展域则可以处理A与B一定不相连的情况。所以不用紧张。
并与查操作
最常用的代码
int Fin(itn v) {return v == f[v] ? v : f[v] = Fin(f[v]);}//log级别
void Uni(int u, int v) {
f[Fin(v)] = Fin(u);//前面有时可以加一些检测操作,比如要合并的节点原来是否就在一个组里边
}
按秩合并(可以很好地维护树的形态与父子关系,可以维护出每个子节点的直接父亲
int Fin(int v) {return v == f[v] ? v : Fin(f[v]);}
void Uni(int u, int v) {//按深度
int fau = Fin(u), fav = Fin(v);
if (fau != fav) {
if (rk[fau] < rk[v]) {
f[fau] = fav;
}
else {
f[fav] = fau;
if (rk[fau] == rk[fav]) rk[fau]++;
}
}
}
void Uni(int u, int v) {//按大小
int fau = Fin(u), fav = Fin(v);
if (fau != fav) {
if (si[fau] < si[v]) {
f[fau] = fav;
si[fav] += si[fau];
}
else {
f[fav] = fau;
si[fau] += si[fav];
}
}
}
扩展域
拓展域是针对于更复杂的合并指令衍生出来的方法。不同域之间对应的数字满足某种特殊的关系,例如第一域的u(u)和第二域的u(u + n)是敌对关系。直接看题分析。
团伙。
该题中需要表达敌人与朋友两种关系,不妨将并查集的数组开大两倍,作为并查集的扩展域,于是可以表达朋友以及敌人两部分,朋友对应第一倍,敌人对应第二倍。于是我们可以得到如下合并公式
//if u and v are friends
union(u, v); union(u + n, v + n);
//if u and v are enemies
union(u, v + n); union(u + n, v);
在该并查集中,v和v + n的关系始终是敌人,因此如果u和v是朋友,我们需要将u和v进行合并,初次之外还应该将u + n和v + n进行合并(u和v是朋友,那么u的敌人和v的敌人也是朋友)。如果u和v是敌人,我们需要将u和v + n进行合并,初次之外还应该将u + n和v进行合并(u和v是敌人,那么u和v的敌人就是朋友,v和u的敌人也是朋友)。
最后计算一下1 ~ n中有多少个连通块即可。
边带权
不难发现所谓的并查集本质上也是一种树,由于路径压缩的存在,使得一个并查集树中,其被压缩过的子节点总是直接指向根节点,于是我们可以给根节点与子节点之间的边进行赋权。这个权值可以表示该节点与根节点之间的距离(像是下面的例题银河英雄传说就是)。
例题
奶酪
题面:
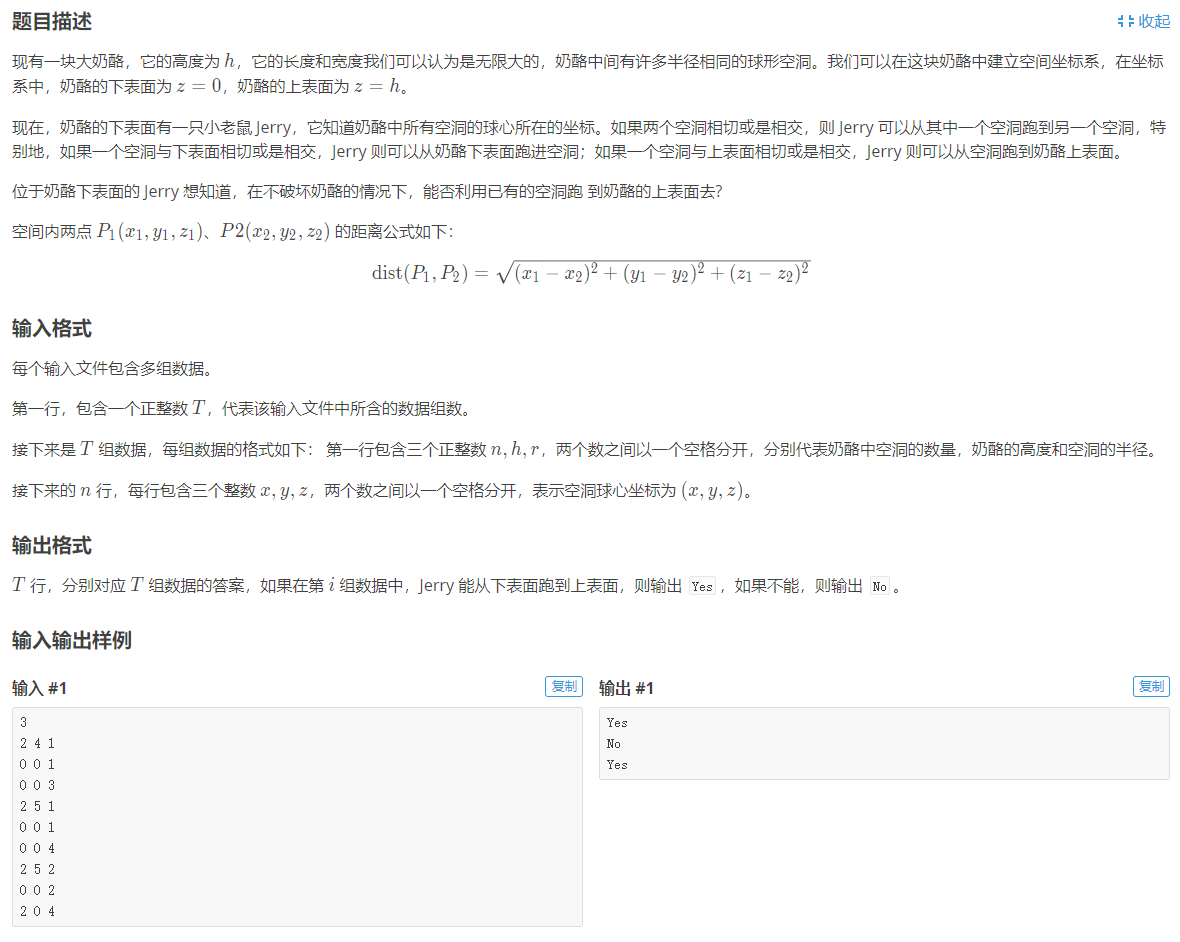
分析:
数据量不算太大,大致上就是每次新增一个洞就判断一下与之前已经判断过的奶酪是否连接,普通的并查集操作。为了方便处理可以初始化f[0] = 0 f[n + 1] = n + 1分别表示下表面与上表面,期间只要判断f[0] == f[n + 1]是否成立即可。
食物链
题面:
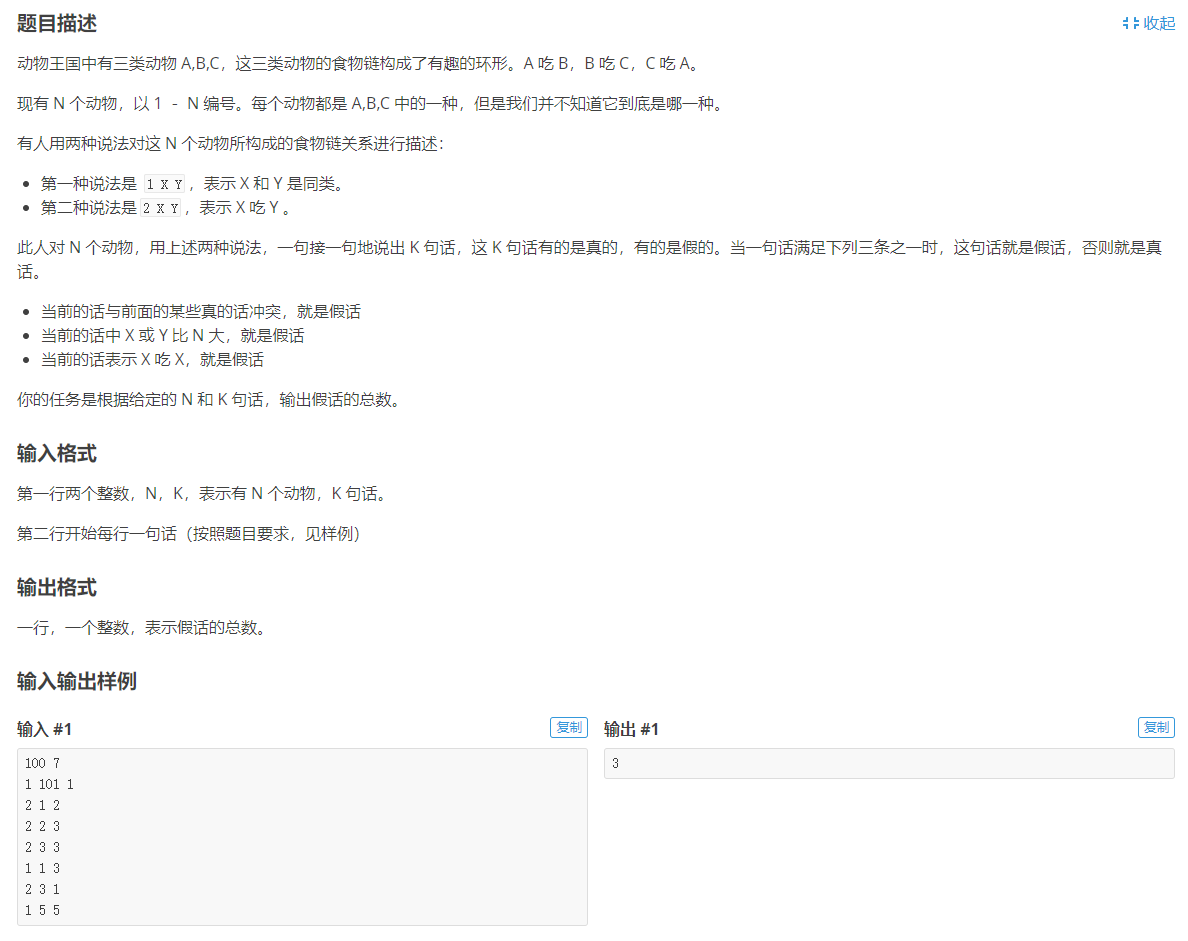
分析:
使用拓展域分出三个域来,分别得到同类,猎物,天敌三个部分。然后得到合并方程
//同类:
union(u, v);
union(u + n, v + n);
union(u + 2n, v + 2n);
//捕食:u eat v
union(u, v + 2n);
union(u + n, v);
union(u + 2n, v + n);
剩下的完善一下就可以了
银河英雄传说
题面:
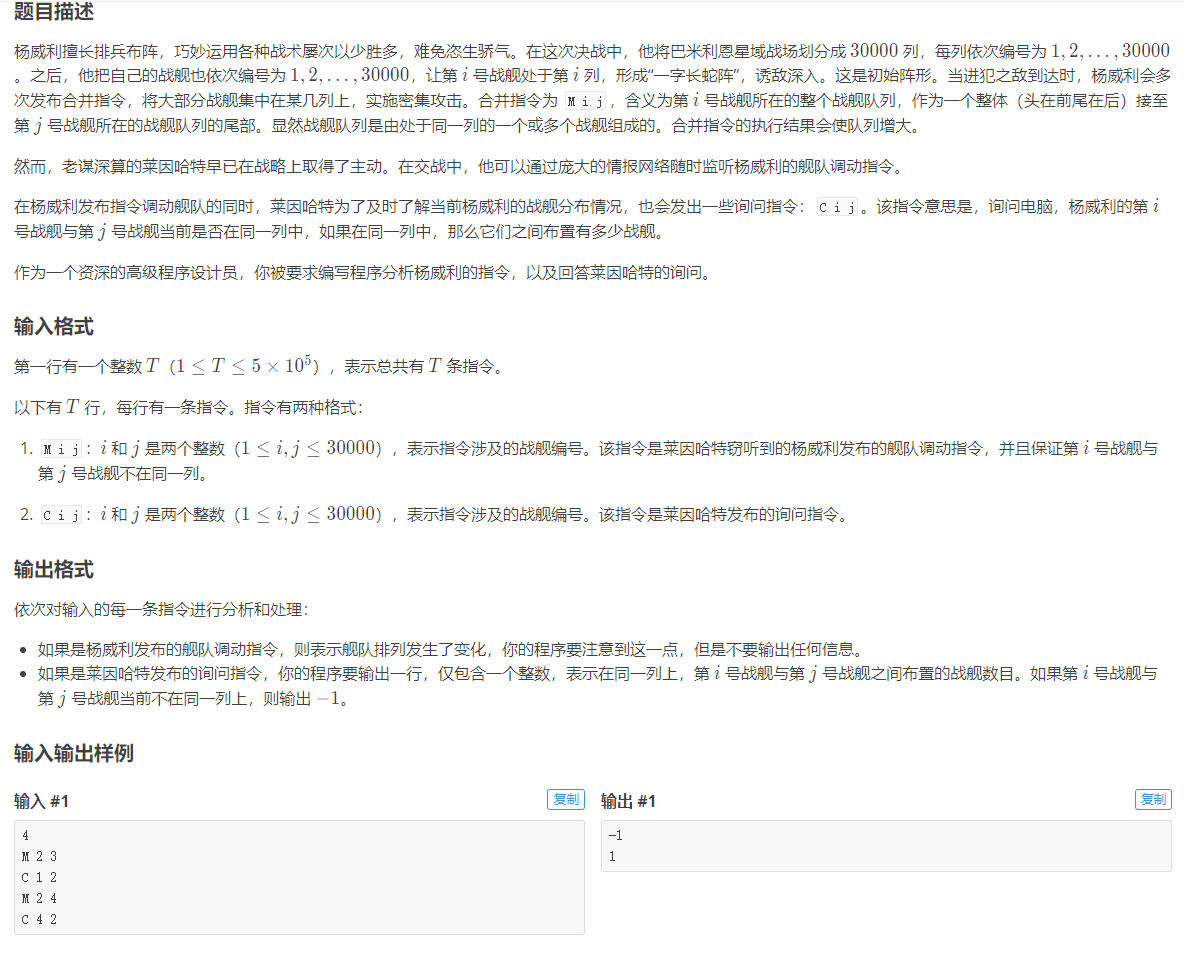
分析:
移动就直接使用并查集的基本操作进行合并,接下来看询问怎么处理。可以得到i,j之间的战舰数为abs(sum[i] - sum[j]) - 1其中sum[i]表示i舰到其舰列头之间的战舰数,可以理解为前缀和的思想。
而sum数组的维护可以在Find函数中进行,得到以下代码,相关解释见注释。
int Find(int v) {
if (v == f[v]) return v;
int fa = Find(f[v]); //记录当前集合的根节点
sum[v] += sum[f[v]]; //由于路径压缩算法中的节点是直接指向其“根节点”(可能未更新)的,所以
//当前节点到最新根节点的距离 = 当前节点到老根节点的距离 + 根节点到最新根节点的距离
return f[v] = fa; //让该节点指向最新根节点,并返回值
}
其思想有点类似线段树中区间修改区间查询的维护操作,将需要维护的信息存储到根节点中,当需要向下进行访问的时候再进行更新
以上是一个静态并查集中维护sum的方法,但是由于集合的规模会变大,深度可能也会变大,所以需要再维护一个数组,size[i],表示当前节点所属集合的节点个数,下面是这道题的核心代码之一。
int Find(int v) {
if (v == f[v]) return v;
int fa = Find(f[v]); //记录当前集合的根节点
sum[v] += sum[f[v]]; //由于路径压缩算法中的节点是直接指向其“根节点”(可能未更新)的,所以
//当前节点到最新根节点的距离 = 当前节点到老根节点的距离 + 根节点到最新根节点的距离
size[v] = size[fa]; //新增代码
return f[v] = fa; //让该节点指向最新根节点,并返回值
}
剩下的就自己动动脑完善一下就可以了。


