算法专题——倍增优化动态规划

倍增优化DP的特点

​ 倍增优化DP通常会将2^k 中的k压入状态方程之中，以表示状态方程其他状态满足某种倍增性质时的结果，例如下面的两个例子，跑路中的dp[i][j][k]可以表示i，j两点之间是否存在一条路径长度为2^k 的路径，开车旅行中的Fun[who][city][k]可以表示who先开，从city出发，开2^k天可以到达的城市。

​ 而转移方程，毫无疑问也与倍增相关，转移方程中，最外层的循环几乎都是循环与倍增有关的变量——k，这一点上可以类比区间动态规划的思想，都是从短(小)的循环到长(大)的。

例题

跑路

题面：

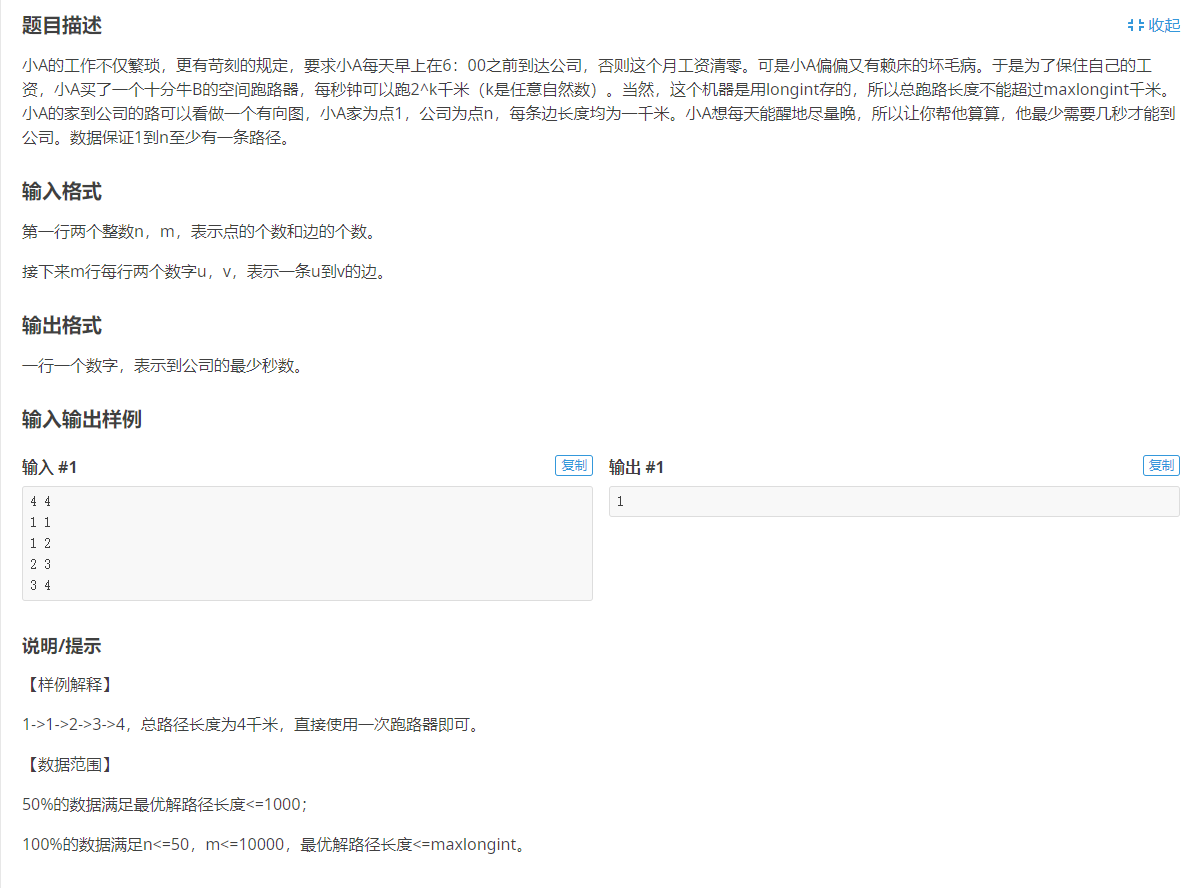
分析：

​ 求家到公司的最短时间，稍微思考一下，发现是求图上两点最短路的变种板，即从原来的最短路，变成了求最短时间，而两者之间的联系——速度（广义），并不是一个恒定值，而是满足于一个规律，即跑2^k m只要一秒，其他距离通过2^k的模式进行合并。

​ 转换转换思维，求两点之间的最短路，需要一个单位进行度量，在这道题中是秒，因此我们要把所有可以在一个单位时间内跑完的路径求出作为求最短路之前的准备工作，进而求出其他需要大于一个单位时间内跑完的路径。

​ 发现数据量并不大，所以可以使用Floyd算法。

​ 于是我们得到状态方程dp[i][j]，表示从i跑到j所需要的最少时间。

​ 那首先是初始化，即上面所说的将所有可以在一个单位时间内跑完的路求出。由于题目给出的都是距离为1(2^0)的点，所以所有可以一个单位时间内跑完的路径2^k一定都可以由两个2^(k - 1)的路径组成，这里就用到了倍增优化的思想（虽然感觉关系不大），于是我们可以类比区间动态规划的思想，从最短的“一单位”路径枚举到最长的“一单位”路径，所以我们可以得到以下方程

for(int k = 0; k < 节点数量; k++)
for(int t = 0; t < 节点数量; t++)
for(int i = 0; i < 节点数量; i++) 
for(int j = 0; j < 节点数量; j++) 
	if (G[i][t][k - 1] && G[k][j][k - 1]) {
		G[i][j][k] = true;
		dp[i][j] = 1;
	}
//G[i][j][k]表示i到j有2^k的路径吗

​ 也可以得到转移方程（Floyd的算法）

for(int k = 0; k < 节点数量; k++)
for(int i = 0; i < 节点数量; i++) 
for(int j = 0; j < 节点数量; j++) 
	dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);

开车旅行

题面：

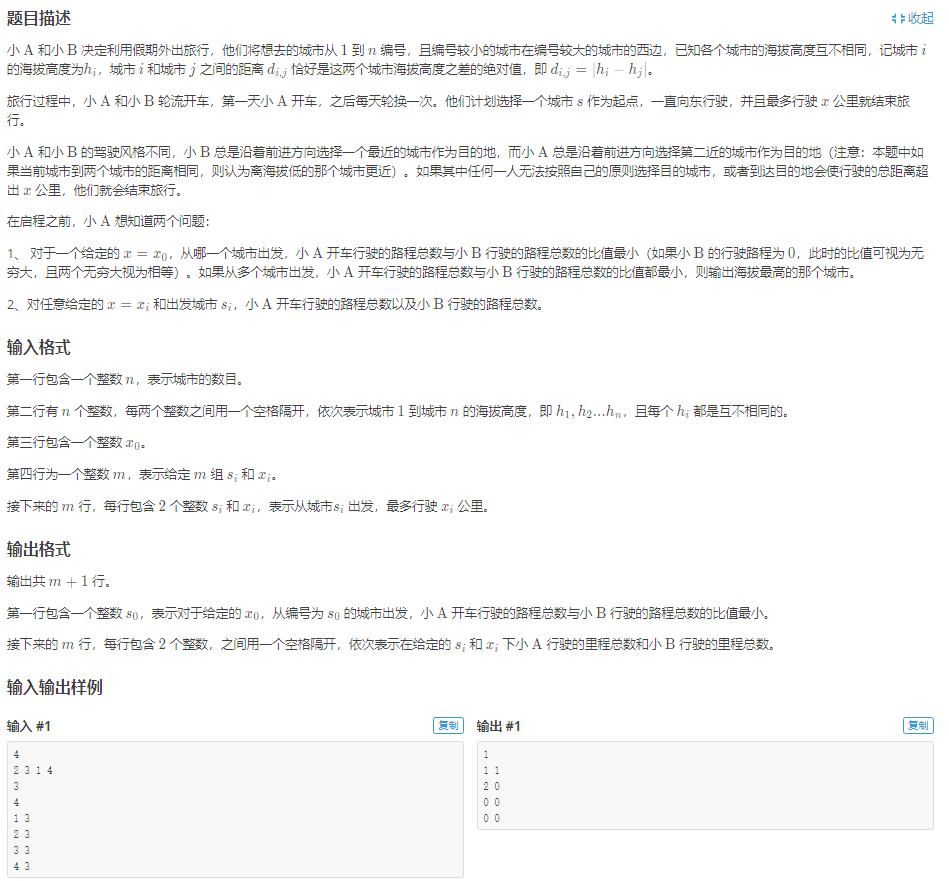
分析：

​ 不难发现，两人从一个固定的城市出发，A(B)先开车，开固定的天数，开到的城市以及距离都是固定的。于是我们可以得到状态方程Fun[who][city][k]表示who先开，从city出发，开2^k天可以到达的城市。同理可以得到dpa[who][city][k] dpb[who][city][k]表示who先开，从city出发，开2^k天，A(B)行驶的距离。

​ 先处理出初始化的问题，倍增算法中注意边界条件的处理，以及初始条件的处理。

​ 首先是边界条件，f[i][j][k]存储的是城市，显然在末端的几个城市，是有无效值的，所以使用数据结构维护当前城市最近的两个点时要考虑该问题，下面是通过集合维护的做法。（摘自题解

struct City
{
	int id,al;//identifier编号,altitude海拔
	friend bool operator < (City a,City b)
    {
        return a.al<b.al; 
    }//重载运算符，按照海拔升序
};//存储城市信息

multiset<City> q;//支持集合内重复元素的set

h[0]=INF,h[n+1]=-INF;
City st;//start
st.id=0,st.al=INF;
q.insert(st),q.insert(st);
st.id=n+1,st.al=-INF;
q.insert(st),q.insert(st);//插入4个初始节点

​ 然后是初始值的问题，见代码示范

for(int i=n;i;i--) {
    ...//预处理
    f[0][i][0]=ga,f[0][i][1]=gb;
    da[0][i][0]=abs(h[i]-h[ga]);
    db[0][i][1]=abs(h[i]-h[gb]);
}

​ 结合倍增算法，我们可以得到转移方程

for(int i=1;i<=18;i++)
		for(int j=1;j<=n;j++)
			for(int k=0;k<2;k++)
				if(i==1)//此时后半段先开车的人和整段先开车的人不同
				{
					f[1][j][k]=f[0][f[0][j][k]][1-k];//整段的路程即后半段到达的路程，后半段的起点即前半段的终点
					da[1][j][k]=da[0][j][k]+da[0][f[0][j][k]][1-k];//整段小A行驶的路程即前半段和后半段小A行驶的路程之和
					db[1][j][k]=db[0][j][k]+db[0][f[0][j][k]][1-k];//整段小B行驶的路程即前半段和后半段小B行驶的路程之和	
				}
				else//此时后半段先开车的人和整段先开车的人相同，其余与上面一样，就不再赘述
				{
					f[i][j][k]=f[i-1][f[i-1][j][k]][k];
					da[i][j][k]=da[i-1][j][k]+da[i-1][f[i-1][j][k]][k];
					db[i][j][k]=db[i-1][j][k]+db[i-1][f[i-1][j][k]][k];
				}
//f → Fun, da → dpa, db → dpb

​ 之后就是怎么通过以上三个方程求解问题，可以写一个方程，实现计算从S城市出发，限制距离为x0，以及默认条件A先开，可以达到的AB最远行驶距离，最后将结果分别存储在la，lb中，该函数运用到的是倍增的算法以及思想。

int la,lb;
  
void calc(int S,int X)
{
	int p=S;
	la=0,lb=0;//初始化
	for(int i=18;i>=0;i--)
		if(f[i][p][0] && la+lb+da[i][p][0]+db[i][p][0]<=X)
		{
			la+=da[i][p][0];
			lb+=db[i][p][0];
			p=f[i][p][0];
		}//倍增模拟前进
}