算法专题——树型动态规划

树形DP的特点

​ ​树形DP通常在树种进行的DP操作，通常需要将节点的编号压入状态方程之中，例如dp[i]可以表示以节点i为根节点的子树可以得到的最大分数。

​ 树形DP的转移方程通常也发生在父节点与子节点之间，详情可以见下面例题。

​ 还有一种树形DP会结合dfs序进行考察，这时候状态方程以及转移方程又不一样，例如下面的加分二叉树，状态方程dp[i][j]表示如果节点i到节点j形成一颗子树，那么可以得到的最大分数为多少。而状态转移方程也是针对于子树的长度进行的。详情见加分二叉树。

例题

没有上司的舞会

题面：

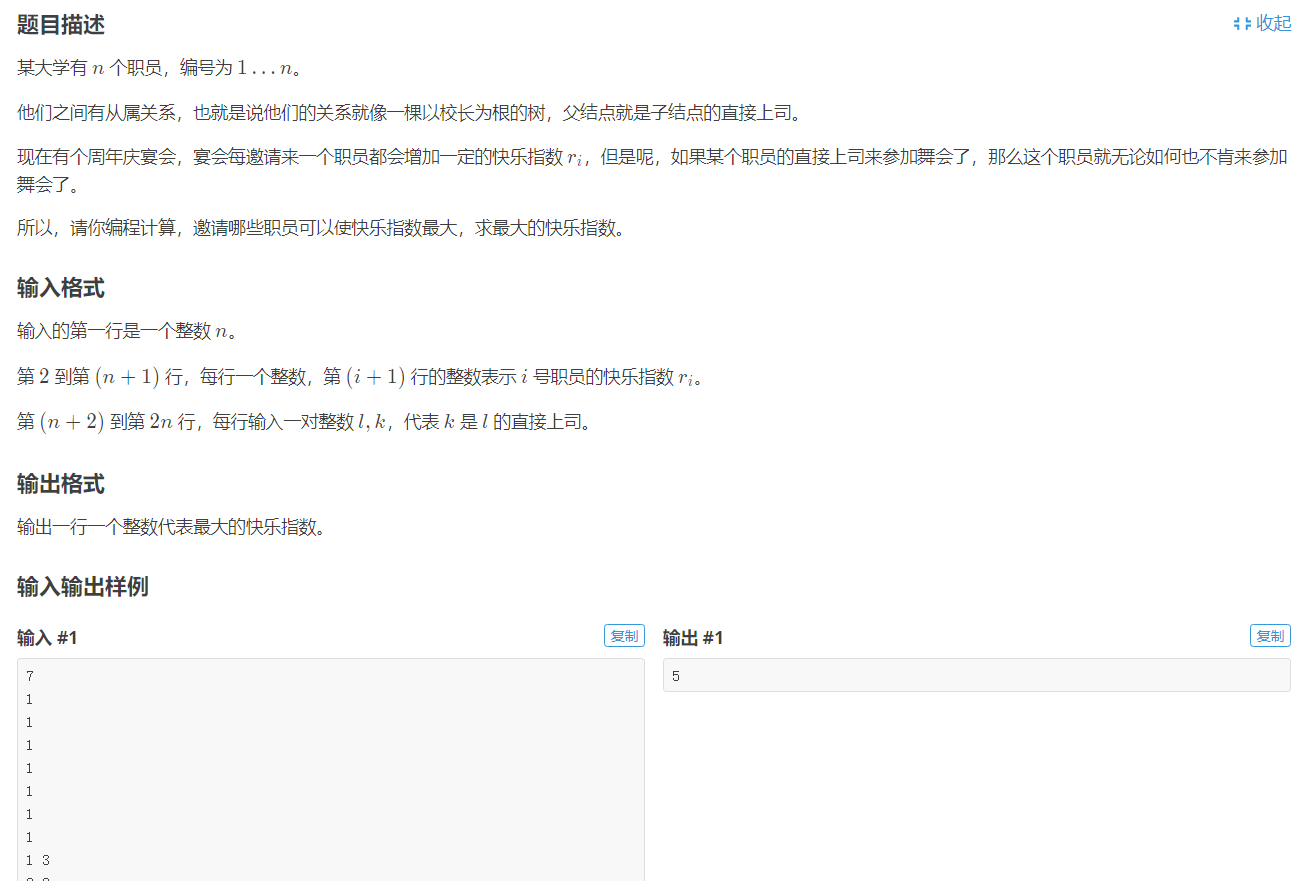
分析：

​ dp[i][0]表示以节点i为根的子树，且i不参加的最大快乐值，dp[i][1] 为i参加的最大快乐值。

​ 很容易可以发现，转移方程发生在子节点与父节点之间，见下

dp[i][1] = sum(dp[son][0]);
dp[i][0] = sum(max(dp[son][1], dp[son][0]));

加分二叉树

题面：

分析：

​ 中序遍历：左中右；前序遍历：中左右。对于1_{N来说，如果其根节点为k，那么其左子树便为1}k - 1，右子树便为k + 1_{n。很显然如果要得到原树1}n的最大加分就应该要得到满足使score(l,k-1) * score(k+1,r)+score[k]最大的根节点以及左右子树，而score(l,k-1) 与score(k+1,r)的大小根据其根节点的位置不同，分数也不一样，而我们要的显然使最大分数的那一个选择，于是我们就将原问题变成了子问题了。即要将求score(i, j)的最大分数变成求score(i, k - 1)与score(k + 1, j)的最大分数。

​ 得到递推方程：

dp[i][j] = max(dp[i][k - 1] * dp[k + 1][j] + val[k]) //dp[i][j]表示节点i到节点j成树时的最大分数，val[k]表示该节点的分数

​ 得到递推方程之后，自然而然的可以想到两种方法实现，一种是dfs记忆化搜索，另一种是仿照区间动态规划的方法解决。

​ 记忆化搜索就是第一题用到的方法，这里不再赘述。而区间动态规划的方法可以参考这篇博客 算法专题——区间型动态规划，大概意思就是最外层循环的内容为树的长度，从1循环到n即可，下面给出大致代码(来自第一篇题解)

for (int len = 1; len < n; ++len) {	//最外层循环，对长度进行循环
		for (int i = 1; i + len <= n; ++i) {//左边界
			int j = i + len;				//右边界
			f[i][j] = f[i + 1][j] + f[i][i];//默认它的左子树为空，如果有的话，这肯定不是最优解
			root[i][j] = i;//默认从起点选根
			for (int k = i + 1; k < j; ++k) {
				if (f[i][j] < f[i][k - 1] * f[k + 1][j] + f[k][k]) {
					f[i][j] = f[i][k - 1] * f[k + 1][j] + f[k][k];
					root[i][j] = k;
				}
			}
		}
}

有线电视网

题面：

分析：

​ 这道题不同于我们前面提到的没有上司的舞会或是加分二叉树，这道题形成的树与分数是有关的，但是要求的并不是可以得到的最大分数，而是在分数非负的情况下让尽可能多的人看直播，此时要求的是最大人数，分数仅是限制条件，而对于这种最终要求的东西以及计算过程中的限制条件我们在dp方程中都是要体现的，于是我们可以得到状态方程

dp[i][j] //表示以节点i为根节点的子树，服务j个人时可以获得的最大分数
//节点，要求的结果以及限制条件分数都在dp中体现了

​ 那接下来，稍微动动脑筋就可以得到递推方程了。代码原理可以参考分组背包，这道题中每一个字节点即为一个组，要做的就是一个个的遍历组，然后进行更新。

for (int i = 0; i < fa.son(); i++) {
	for(int j=fa.size(); j > 0; j--) {			//fa.size()表示父亲节点目前最多可以服务的客人数量
        for(int k = 1; k <= son.size(); k++) {	//遍历当前子节点最多可以服务的人
            if(j - k >= 0) 
                dp[u][j]=max(dp[u][j],dp[u][j-i]+dp[v][i]-edge[k].w);
        }
    }
}

骑士

题面：

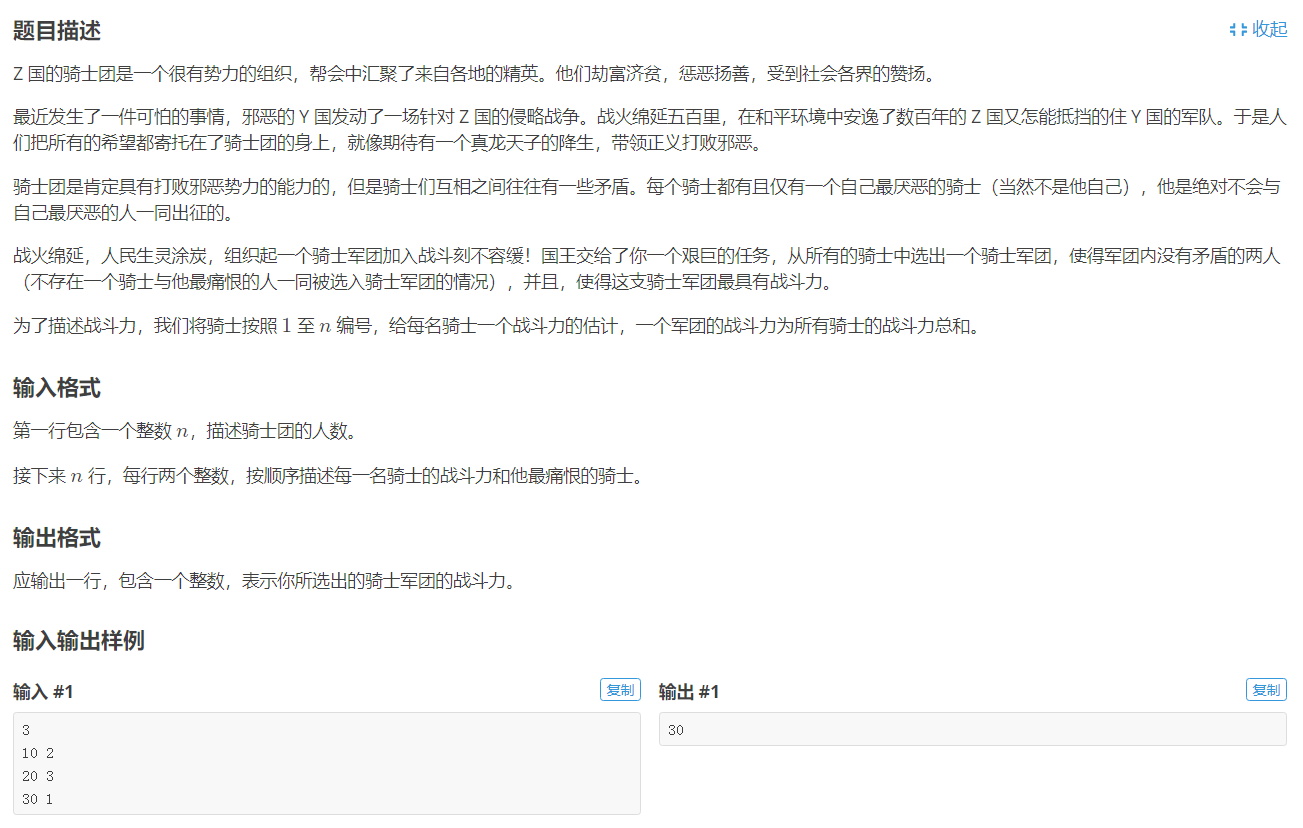
分析：

​ 虽然说是一个图，但其实就是一颗树多加了一条边（一般称这种树为基环树）。在原有的树中添了一条边便会形成环，在普通的DP中如果成环了，往往需要解环操作，这道题的解环操作稍微想想也可以想到，取环上两个相邻的节点，分别进行树上DP。状态方程和转移方程基本可以类比前面讲过的“没有上司的舞会”，于是我们可以得到最终的答案为ans = max(dp[i][0],dp[j][0]);其中i和j分别为上述说的环上任意两个相邻的节点。至于为什么是这样也非常好理解，因为i和j不可得兼，所以一定要其中一个不出场，当其中一个不出场时可以发现此时的图等价于将多添的那条边产生的影响去掉了，所以可以直接使用树形DP的方法求解，最后便是从两个答案(i不去或j不去)之中选了。