算法专题——kmp算法
KMP的特点
KMP算法是一种字符串匹配算法,但其常见的应用除了两个字符串之间的匹配之外,还有求解一个字符串的最长相等前后缀,循环节等应用。KMP的核心在于nxt数组.
本文基于读者对kmp算法有一定了解的基础上,对kmp的原理以及二级结论进行讨论。
下面进行讨论.
NXT数组的含义
1. 从匹配的意义上看NXT数组的含义.
我们知道, 不管是在求一个字符串NXT数组, 还是在利用NXT数组求两个字符串的匹配问题时, 每当字符串不匹配, 都需要退回到当前节点的NXT数组的位置再进行两个字符串的匹配. 所以可以从字符串匹配的角度思考NXT数组的含义.
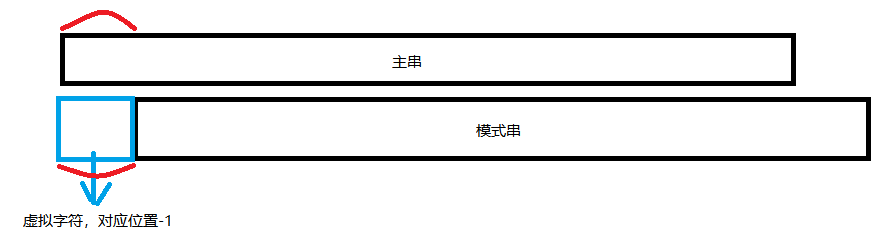
NXT数组是字符串自己与自己匹配得来的, 于是先将主串复制一份得到模式串. 并在模式串前面加一个虚拟字符, 对应下标为-1(蓝色框部分), 定义该虚拟字符为万能匹配字符(即可以匹配所有字符的字符). 下面对匹配的过程进行剖析.
-
先从一般的情况入手, 如下图所示, 当
i指向如图所示位置,j指向nxt[i]位置时, 可以得到nxt[i]与i的对应关系为, 主串中的红色曲线框取部分(后缀序列[i - nxt[i], i])与模式串中的红色曲线框取部分(前缀序列[0, nxt[i]])是两个长度相等的序列, 并且两个序列中的紫色圆圈部分完全匹配, 使得符合这两个条件的相同序列最长, 即可得到i对应的位置nxt[i].于是当字符串在
i位置不匹配时,可以跳转到nxt[i]的位置继续进行匹配。如此便可以避免i重新回到起点,即利用已经匹配过的部分减少不必要的匹配次数。

- 然后再谈起始情况, 起始情况, 将两个串进行对其, 得到
i = 0, j = -1. 如下图所示, 由于模式串多出一个虚拟字符, 所以对齐之后会多出一个字符位. 根据上面提到的两个条件, 长度相等, 以及紫色圆圈部分完全匹配, 可以得到红色部分, 这时候紫色圆圈部分长度为0,因此从匹配跳转的意义上看i会直接跳转到j的位置。进而可以得到,nxt[0] = -1.
2. 从后缀的意义上看
NXT数组同时也存储了字符串公共前后缀的最大长度,, 在上面提及的NXT数组匹配上的意义上可以发现,
从匹配的意义上看时,我们发现主串与模式串的紫色部分完全相等, 而又两串本质为同一串, 于是可以联想到相等前后缀的关系。而天然的字符串都是从零开始的,所以nxt[i]数组的值天然的会与紫色圆圈部分的长度相等,从而nxt[i]数组可以记录最长相等前后缀的长度, 因此每一个本来是存储跳转关系信息的红色圆圈部分, 也同时会存储下紫色圆圈部分可以延伸的最远的长度, 这是由字符串是从零开始决定的, 即nxt[i]存储了以i - 1为终点的最长相等前后缀。要注意的是, 这里在记录长度时并不包含蓝色虚拟字符在内。
所以在实际应用中,我们也经常会用KMP解决公共前后缀的问题.
代码实现
关于虚拟字符, 由于虚拟字符是万能匹配的, 所以当模式串的下标指向虚拟字符时, 总是能够匹配成功, 所以需要进行一个特判. 最后就可以得到对应的代码了.
void Getnext(int nxt[], char str[]) { //下标从0开始
int i = 0, j = -1;
nxt[0] = -1; //初始条件,特殊处理
while(i < len)
if(j == -1 || str[i] == str[j]) nxt[++i] = ++j; //紫色圆圈末端相等, 给红色框取部分末端的nxt数组进行标记
else j = nxt[j]; //紫色圆圈末端不相等,那j应该回到nxt[j]
}
void Getnext(int nxt[], char str[]) { //下标从1开始,
int i = 0, j = -1, len = strlen(str);
nxt[0] = -1;
while(i < len)
if(j == -1 || str[i + 1] == str[j + 1]) nxt[++i] = ++j; //可以理解为主串加了一个虚拟字符和模式串加了两个虚拟字符
else j = nxt[j];
}
串串匹配
核心代码
while (i < slen && j < len) //从0开始
if (j == -1 || strs[i] == str[j]) i++, j++; //如果匹配,就匹配下一个字符
else j = nxt[j]; //不匹配,j回到上一个可以比较的值
知道一个串的NXT数组之后就可以开始进行串与串之间的匹配了. 这部分较为简单直接, 就略去了. j为1的含义可以参考上面虚拟字符的使用.
最长相等前后缀
从上面的NXT数组的含义中, 已经很显然的表明了其可以求一个串的最长相等前后缀的功能, 直接取nxt[len]即可. 不多赘述.
循环节
最小循环节
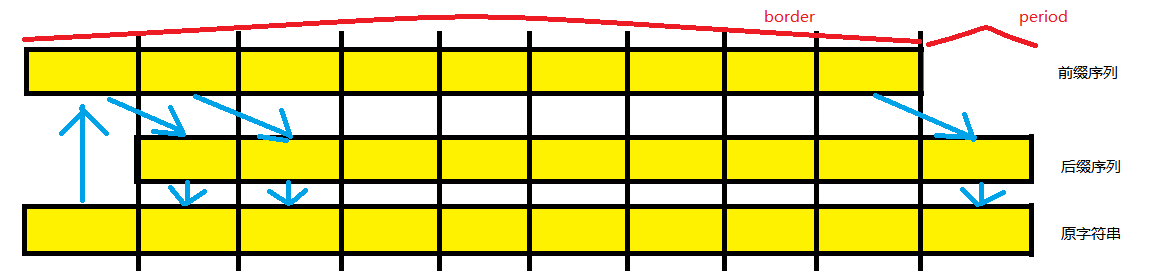
kmp可以用于求一个字符串的循环节, 图示如下, 第三个长方形表示原串, 第一二个串表示原串中匹配的前后缀部分, 其长度为nxt[str.length]. 如果len % (len - nxt[len]) == 0则可以发现, 通过其对称性, 可以将原串拆分为一个个黄色的子段, 其长度为len - nxt[len], 即为原串的最小循环节(nxt[len]会取尽可能大的值, 循环节因此也会得到尽可能小的长度).
因此可以说如果满足len % (len - nxt[len]) == 0, 则原串可以分解为长度为len - nxt[len]的循环节. 蓝色箭头是简单的推导示意图, 即表示指向的两个连续子序列具有完全相同的关系.
周期(广义循环节)
探讨更一般的情况, 如果len % (len - nxt[len]) != 0, 则原串的循环节为原串本身, 不再拥有长度小于原串的循环节. 下面会给出证明.
对于这种更一般的情况, 我们给出下面定义
若 0 < p ≤ |s|, s[i] = s[i + p], ∀i ∈ {1, · · · , |s| − p}, 就称 p 是 s 的周期 (period)。注意周期不一定是循环节
若 0 ≤ r < |s|, pre(s, r) = suf(s, r), 就称 pre(s, r) 是 s 的border。
pre(s, r) 是 s 的 border ⇔ |s| − r 是 s 的周期。
比如
abaaaba就有周期 4, 6, 7, 对应的 border 是aba,a, 和ϵ。
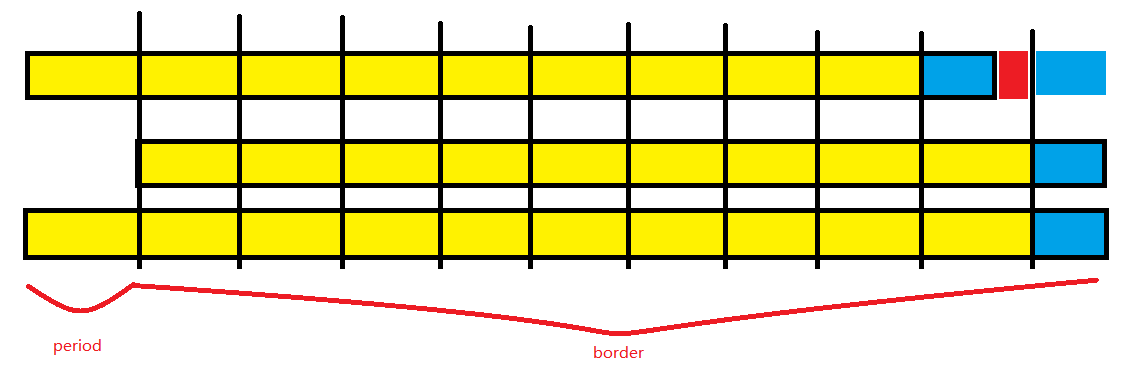
可以发现黄色块已然不是原创的循环节,但是原字符串去掉尾段的蓝色块后,剩下的部分仍然可以被黄色块循环(证明方法同上面的循环节)。所以我个人也会将period(黄色块)称为广义循环节.
Weak Periodicity Lemma
p 和 q 是字符串 s 的周期, p + q ≤ |s|, 则 gcd(p, q) 也是 s 的周期。
证明: 令 d = q − p (p < q), 则由 i − p > 0 或 i + q ≤ |s| 均可推出 s[i] = s[i + d], 继而类比辗转相除法的内容可以得到s[i] = s[i + gcd(q, p)]
对于有疑问的点, 不妨拿张草稿纸手推一下.
Periodicity Lemma: p 和 q 是 s 的周期, p + q − gcd(p, q) ≤ |s|, 则 gcd(p, q) 也是 s 的周期。

一个重要的引理: 字符串 s 的所有不小于 |s|/2 的 border 长度组成一个等差数列, 公差为
len - nxt[len], 即一个period1的长度. border可以表示为nxt[nxt[nxt[...nxt[len]]]]
证明: 设 s 的最大 border 长度为 n − p, (p ≤ |s|/2), 另外某个border 的长度为 n − q, (q ≤ |s|/2), 则 gcd(p, q) 是 s 的周期, 即 n − gcd(p, q) 是 s 的 border 长度, 于是 gcd(p, q) ≥ p ⇒ p | q。
由上述引理得到的一个小结论:当满足len % (len - nxt[len]) != 0, 即第一个period不是循环节时,字符串往后的period都不可能是循环节, 原串不会拥有长度小于原串的循环节.
证明: 将黄色块以蓝色块加红色块的方式表式, 可以得到下图. 根据上面的引理可以发现对于border而言,有nxt[len] == nxt[nxt[len]] + 黄色块的长度, 即nxt[nxt[len]]会指向this的地方, 又黄色块不是原串的循环节, 结合一点整除理论的知识点可以得到, 不管广义循环节在多加几个黄色块都不会是原串的循环节.

证明的另一种说法
nxt[len]与nxt[nxt[len]]的关系满足nxt[len] == nxt[nxt[len]] + 黄色子段的长度. 可以得到图二所示的紫色椭圆部分即为nxt[nxt[len]]. 而直接从图示中就可以直接得出结论如果len % 蓝色 != 0, 那么len % (蓝色 + 黄色) != 0也显然成立, 所以对于nxt[nxt[len]]以及更深的嵌套都不会满足len % (len - nxt[len]) == 0的条件

串串匹配中的一个引理
引理: 字符串 u, v 满足 2|u| ≥ |v|, 则 u 在 v 中的所有匹配位置组成一个等差数列。
证明: 只需讨论至少匹配 3 次的情况。考虑 u 在 v 中的(最左边)第一次和第二次匹配, 间距为 d。另外某次匹配与第二次匹配的间距为 q。
可知 d, q 都是 u 的周期, 从而 r = gcd(d, q) 也是 u 的周期。设 u 的最小周期为 p ≤ r。 由 p ≤ r ≤ q ≤ |u1 ∩ u2| 知 p 也是 u1 ∪ u2 的周期。若 p < d, 则 u1 右移 p 的距离也产生一次匹配, 矛盾。
于是 d ≤ p ≤ r = gcd(d, q) 即 p = d, d | q。

例题
PACM TEAM
分析: 双哈希, 或者kmp找规律解决


