算法学习——莫队算法
莫队算法学习笔记
莫队的特点
简单的莫队算法是用于离线维护一个区间（或是一个区间内的数据结构）的算法，下面将就最简单的莫队算法——区间的离线处理进行介绍。
这里直接贴一道模板题HH的项链，题意简单理解为询问区间内有多少不同的数字。
先考虑直接暴力的算法，即询问到什么区间就扫一遍该区间，时间复杂度为O(n)，m次询问，则总复杂度为O(nm)。
这种方法显然过于简单粗暴，我们换一种暴力的算法进行思考。不难看出每一个询问都并非是完全独立没有关联的，不难发现两个询问之间如果有区间重合，两个询问间的答案也必然有一些关系。以一个极端的例子为例，对区间[l, r]的询问与对区间[l, r + 1]的询问，两个询问之间相差了一个元素，那么只要判断多出的这一个元素是否影响最终的结果即可。（下为伪代码）
if (a[i]在[l, r]没出现过)
query[l, r + 1].ans = query[l, r].ans + 1;
以此类推，如果已经知道了[l, r]的答案，可以在O(1)时间复杂度内查询到[l - 1, r]，[l + 1, r]，[l, r - 1]，[l, r + 1]的答案。以此类推，如果知道了[l, r]的答案，想要得到[l', r']的答案，需要移动|l - l'| + |r - r'|步，即时间复杂度为O(|l - l'| + |r - r'|)。这个公式显然就是曼哈顿距离，将每一个询问都映射为二维平面上的一个点的话，任意两个询问之间的转移步数就是两点之间的曼哈顿距离。要在最短时间内处理m个询问，显然应该按照(曼哈顿)最小生成树的边对询问(每一个点)进行处理，但是这种最小生成树的算法过于冗长与复杂，这里不进行介绍(我不会，之后如果学会了再来进行补充)。
我们讲另一种方法——分块处理。曼哈顿将询问抽象为二维平面上的一个点，分块算法则是将询问仍是做一个区间，可以将上一段从“这个公式显然……”开始的说明去掉。时间复杂度为O(|l - l'| + |r - r'|)，那么应使两个询问的移动尽量的小，那么可以想到对询问进行排序，当按序处理问题时使移动的步数尽可能的小。但是应该怎么排序，不能单纯的以左端点或右端点进行排序，因为最坏的情况下右端点会反复横跳，时间复杂度很高。于是我们想到对区间进行分块，将其分成√n块(共√n个这样的块)，以左端点所在的块为第一关键字，以右端点为第二关键字进行排序，这样排好序后，相邻询问之间的移动距离会相较于单纯的以左端点或右端点进行排序更少，时间复杂度为O(n√n)，下为简单证明。
分块相同时，右端点递增是
的，分块共有
个，复杂度为
分块转移时，右端点最多变化
，分块共有
分块相同时，左端点最多变化
，分块转移时，左端点最多变化
，共有
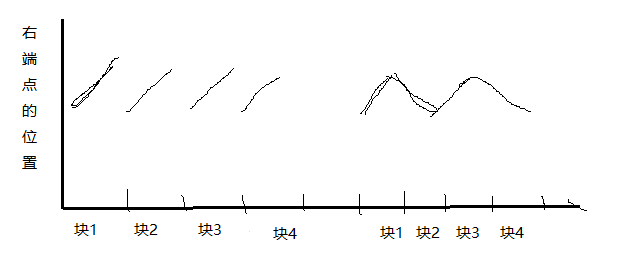
例外可以在原有的基础上进行一个简单的优化。对奇偶块的右端点进行不同的排序，奇块右端点升序，偶块右端点降序。这种排序较之与原来的排序的优点在于，在跨块时，右端点可以不用重新跑回最左端，再慢慢移动到最右端，而是可以从最右端慢慢移动到最左端。下面的图便于理解。
