PointNet、PointNet++和Frustum PointNet

简介

这是在阅读完Ruizhongtai Qi的博士论文《DEEP LEARNING ON POINT CLOUDS FOR 3D SCENE UNDERSTANDING》后的一篇读书笔记。这篇论文的整体框架如下图所示，其中涉及的几项工作在点云处理领域都是非常有影响力的。

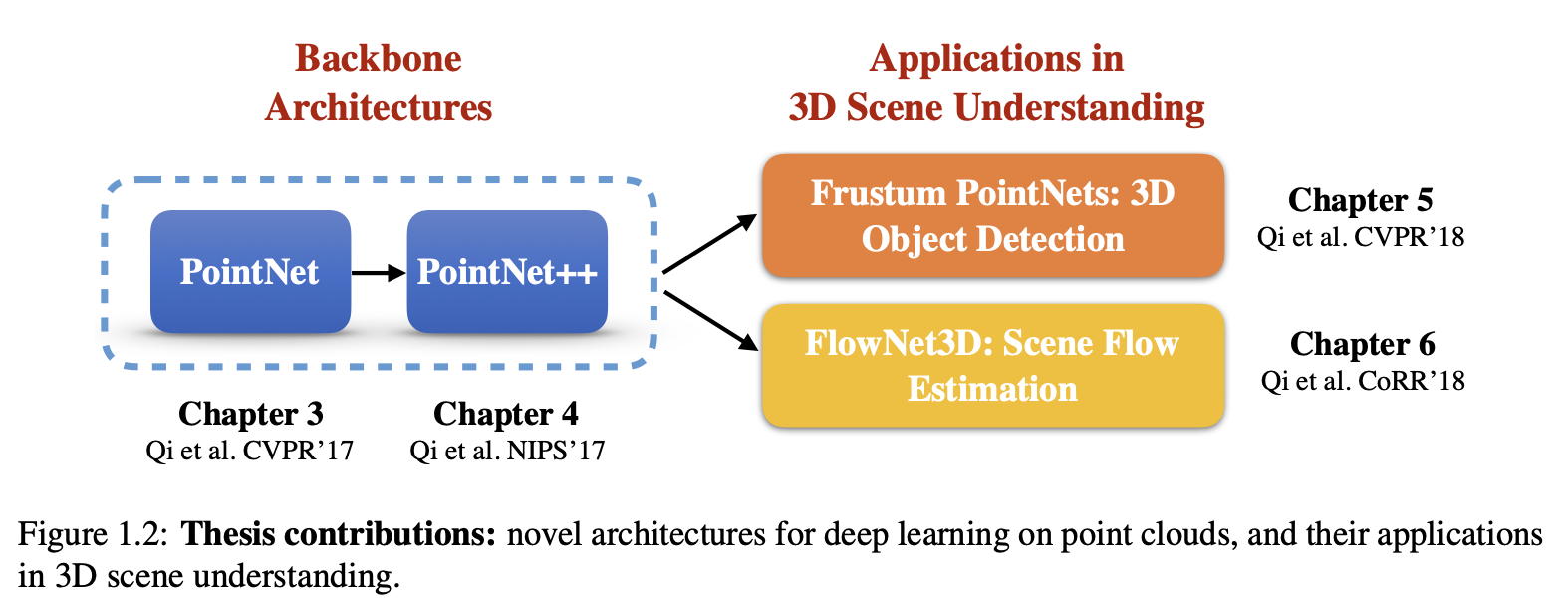
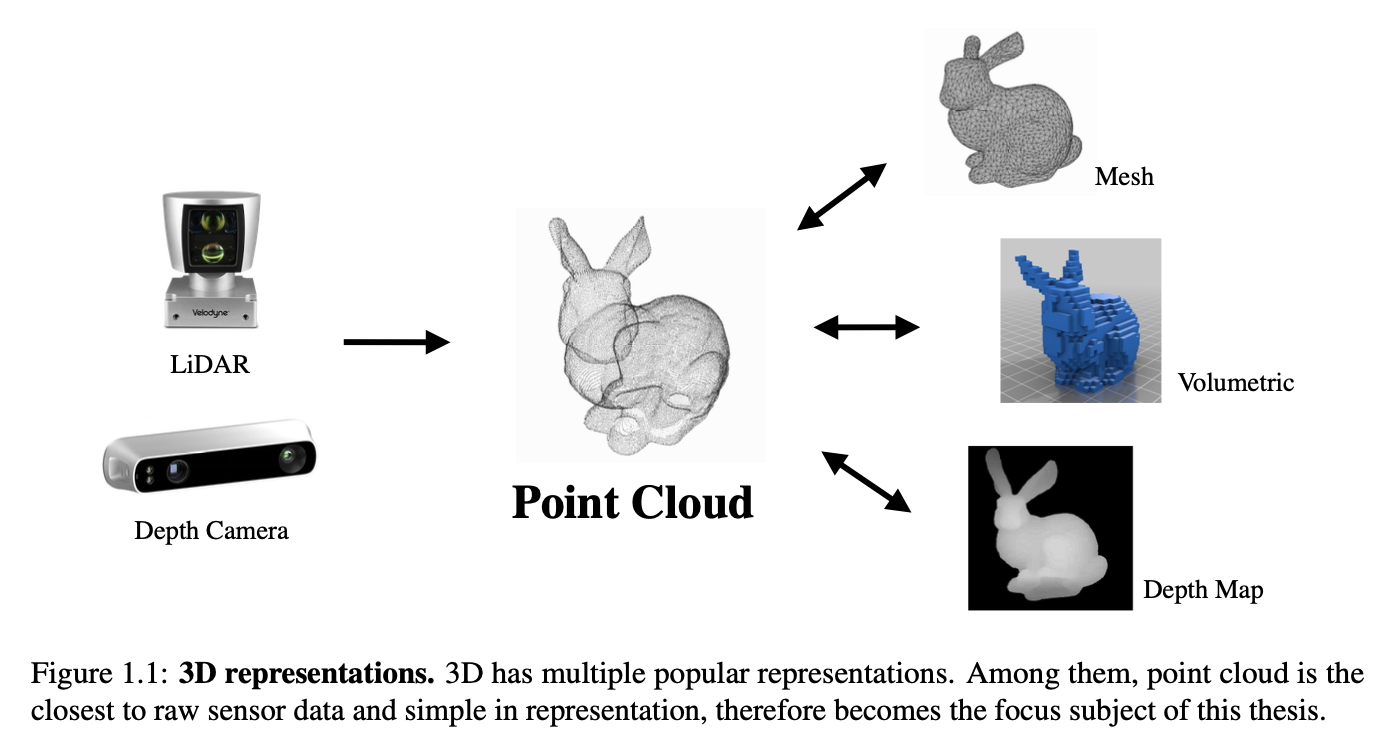
3D场景有很多表示形式，其中点云是最接近raw sensor data的数据形式，且不会像volumetric表示那样产生量化误差，或像multi-view表示那样产生投影误差。论文中涵盖的4项工作都是对点云数据的处理，这篇笔记主要对前3项工作进行了记录。

1 PointNet

PointNet是一个用来处理点云数据的通用框架，可用来做分类、部件分割、语义分割等任务，其架构如下图所示。

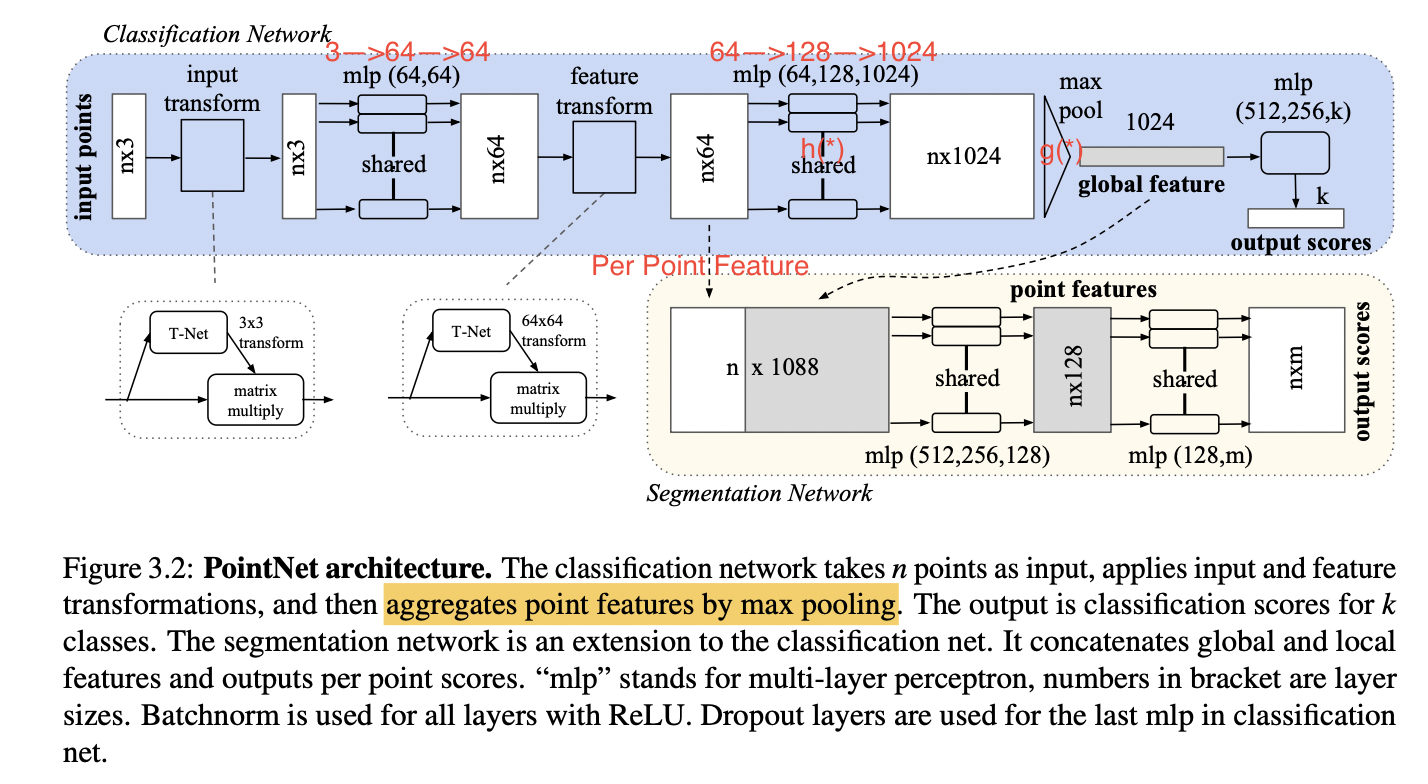
PointNet的输入是一个点集，这个点集可能表示某个场景下的某个物体，那么PointNet应该具备以下几个特点：

• 点集的置换不变性：改变点的输入顺序，不影响输出结果。比如不论输入是\(\{P_1, P_2, P_3, P_4\}\)，还是\(\{P_3, P_1, P_2, P_4\}、\{P_4, P_3, P_2, P_1\}\)。模型应该将点集所表示的物体预测成同一类。

A network that consumes N 3D points needs to be invariant to N! permutations of the input set in data feeding order.

• 点集的刚体变换不变性：对所有点做同一rigid transformation(R/T)，模型的预测结果不变。

As a geometric object, the learned representation of the point set should be invariant to certain transformations. For example, rotating and translating points all together should not modify the global point cloud category nor the segmentation of the points.

为了满足上述两个特点，PointNet做了下面两点结构设计：

• 对无序点集具有置换不变性的对称函数
  
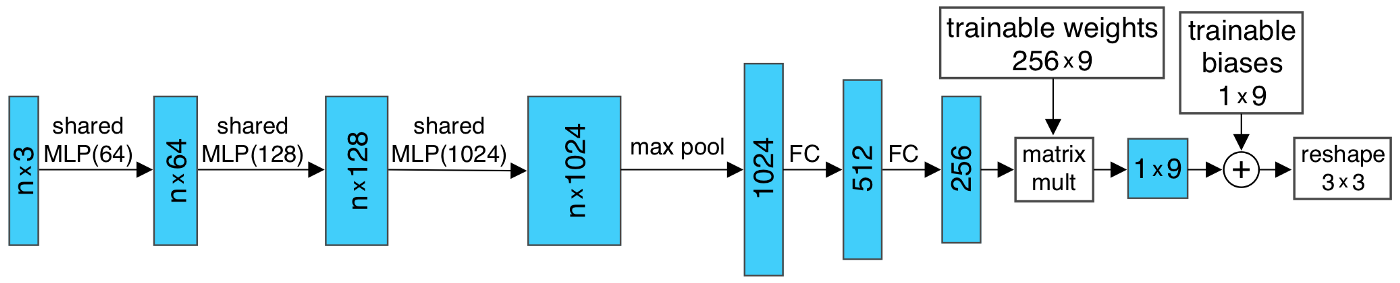
  其中h函数就是Figure 3.2的 shared MLP，g函数是Max Pooling操作。
• 用于表示刚体变换的T-Net
  

参考资料：
《An In-Depth Look at PointNet》

2 PointNet++

PointNet有一个缺陷：无法捕获local content。因为要么是shared MLP作用在每个point上，要么是max pooling对全部点的信息进行summarize。为了解决PointNet的这一缺陷，作者设计了PointNet++这一分层神经网络，其核心思想是在局部区域递归地应用PointNet，如下图所示：

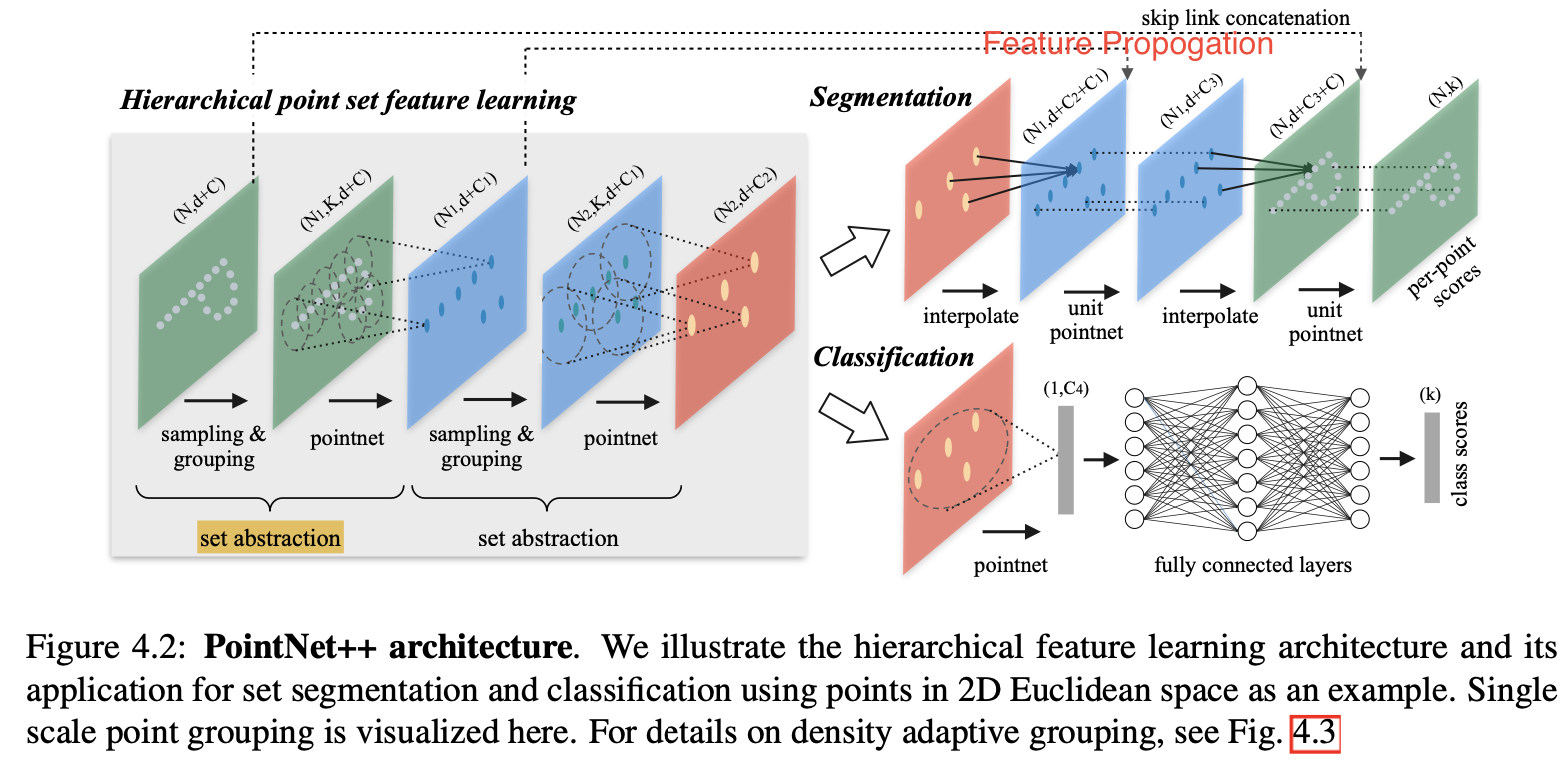
PointNet++的核心组成主要包括上图左半部分的set abstraction和右半部分的feature propogation：

• Set Abstraction Level

  • Sampling Layer：使用Iterative Farthest Point Sampling(FPS)进行采样，从而确定每个group的中心点。
  • Group Layer：在group的中心点的基础上，选取candidate point形成一个group，这个group的点云数据作为PointNet的输入。
  • PointNet Layer：这层没啥可说的，就是上面PointNet这节的内容。

• Feature Propogation Level

  • Interpolation Layer

  We use inverse distance weighted average based on K-nearest neighbors(as in Eq.4.2 in default we use p=2, k=3). The interpolated features on points are then concatenated with skip-linked point features from the set abstraction level.

  

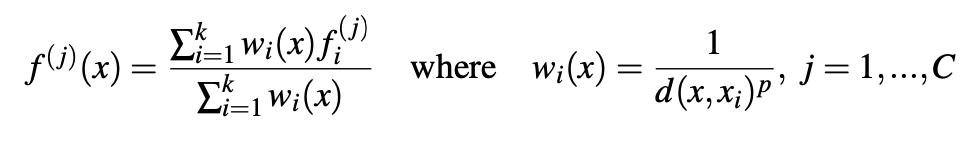
  • Unit PointNet Layer

  Then the concatenated features are passed through a "unit pointnet", which is similar to one-by-one convolution in CNNs.

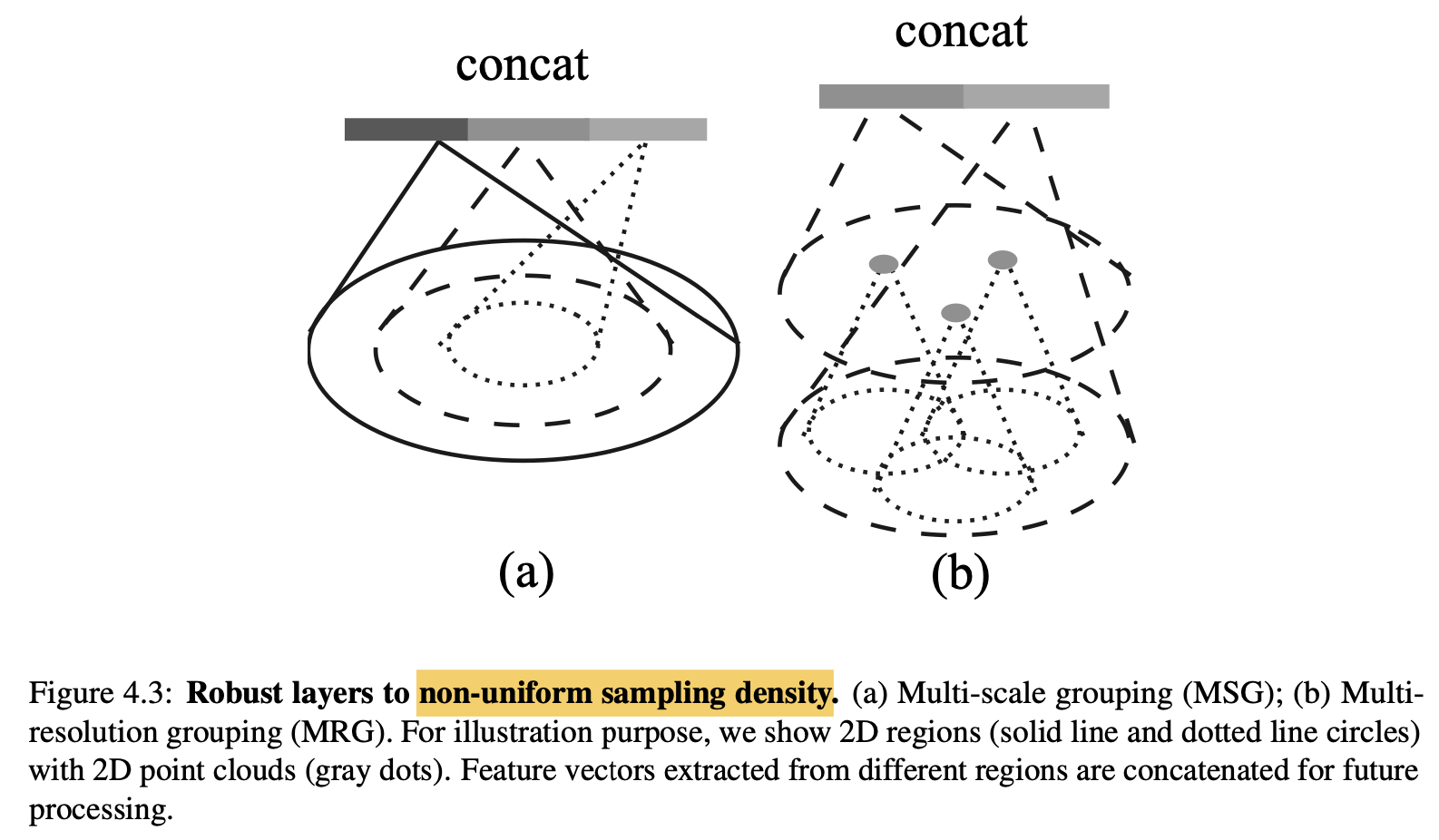
点云数据有一个很显著的特点——在不同区域点云的密度不一样。比如通过Lidar采集的点云数据，通常距离较远地方的点云较稀疏。这种分布不均的特性给点云的特征学习带了了很大的挑战，PointNet++对PointNet Layer做了改进，提出两种density adaptive PointNet Layer——Multi-Scale Grouping(MSG)和Multi-Resolution Groupint(MRG)。

3 Frustum PointNet

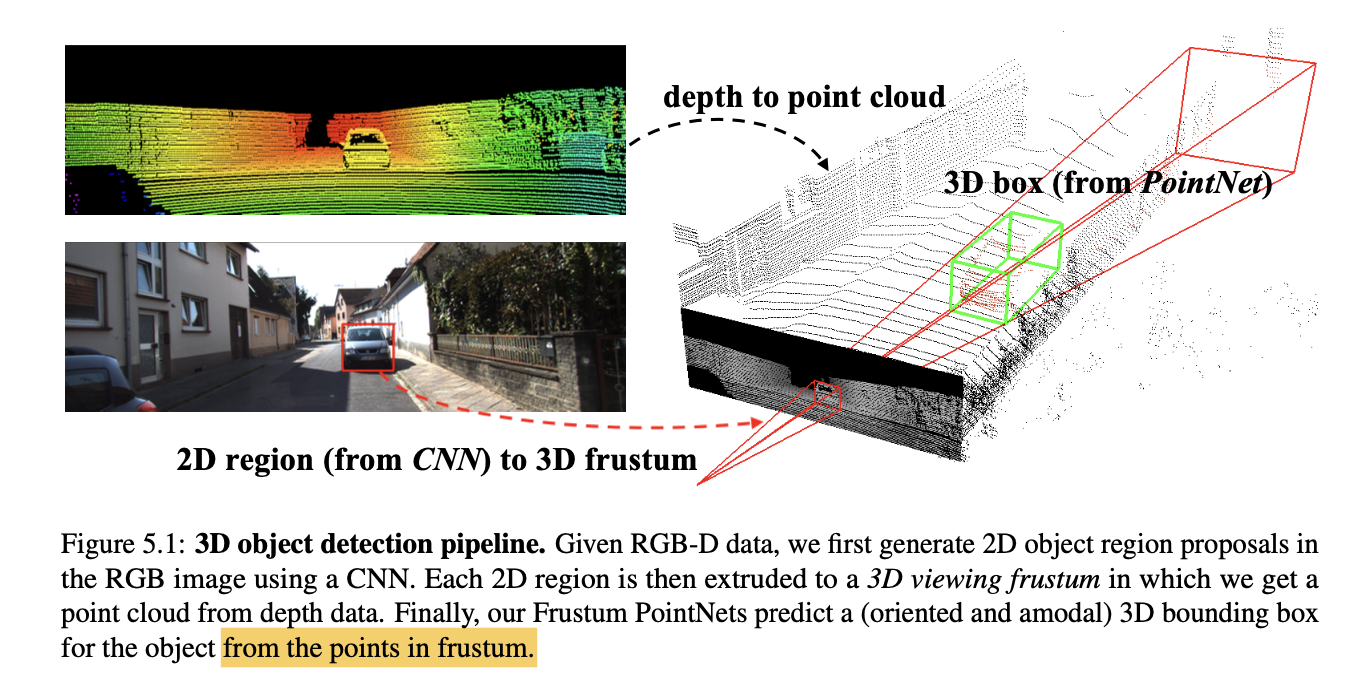
在3D物体检测中，如果像2D物体检测一样在3D空间中枚举可能的BBox，会消耗大量计算，难以达到实时3D检测。如何在3D空间中找到可能的3D BBox是一个关键挑战。
如下图所示，Frustum PointNet在基于2D检测结果形成的截头锥体中搜索可能的3D BBox，大大缩小了搜索空间，减小了计算量。

我们知道2D的BBox可以用参数\((c_x, c_y, h, w)\)来描述，3D BBox需要更多的参数进行描述：

The 3D box is parameterized by its size \(h,w,l\), center \((c_x, c_y, c_z)\), and orientation \(q,f,y\) relative to a predefined canonical pose for each category. In our implementation, we only consider the heading angle q around the up-axis for orientation.

下图描绘了Frustum PointNet进行3D物体检测的整体流程：

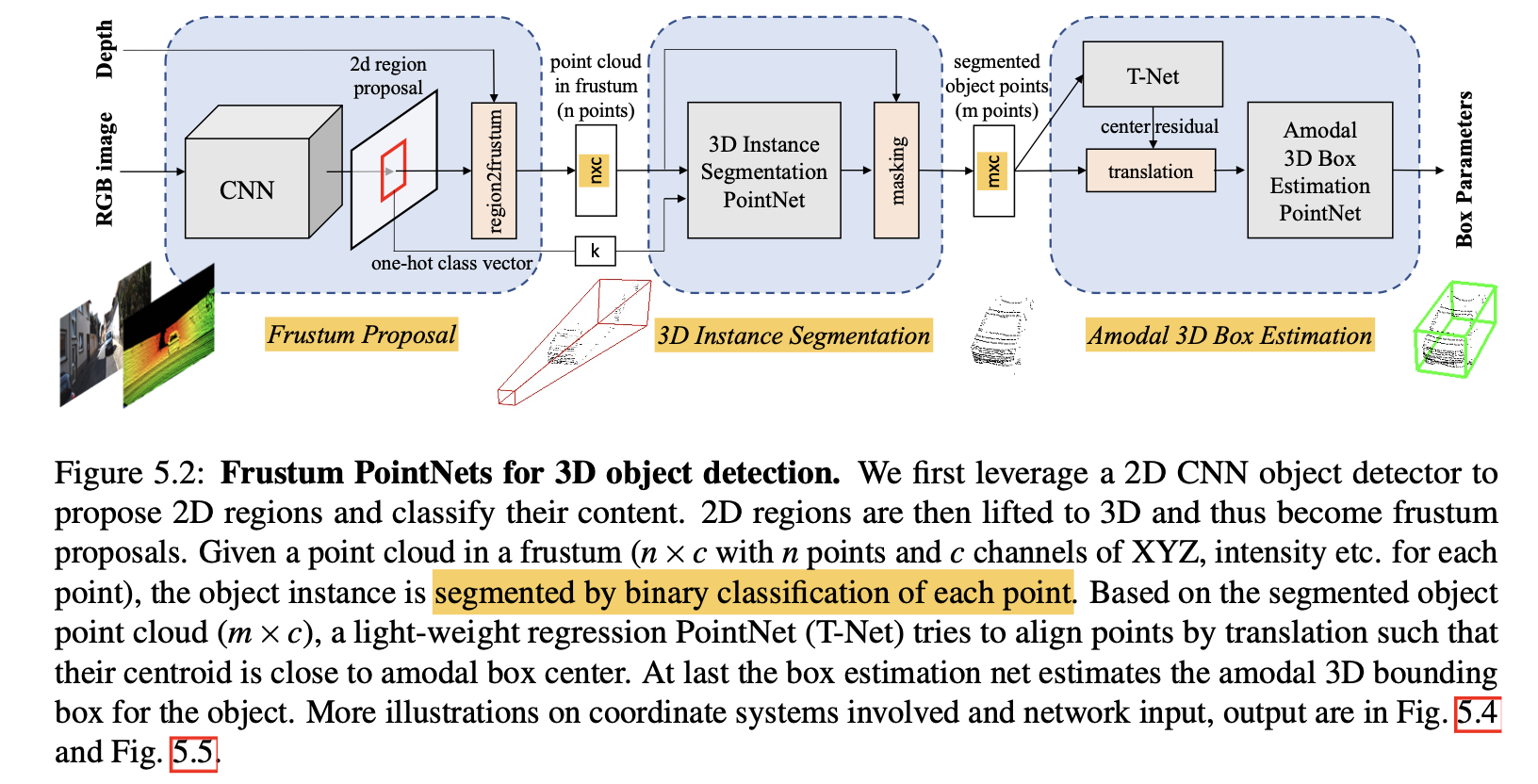
整个流程可以分成Frustum Proposal、3D Instance Segmentation和Amodal 3D Box Estimation3个阶段。各阶段的网络结构如下图所示：

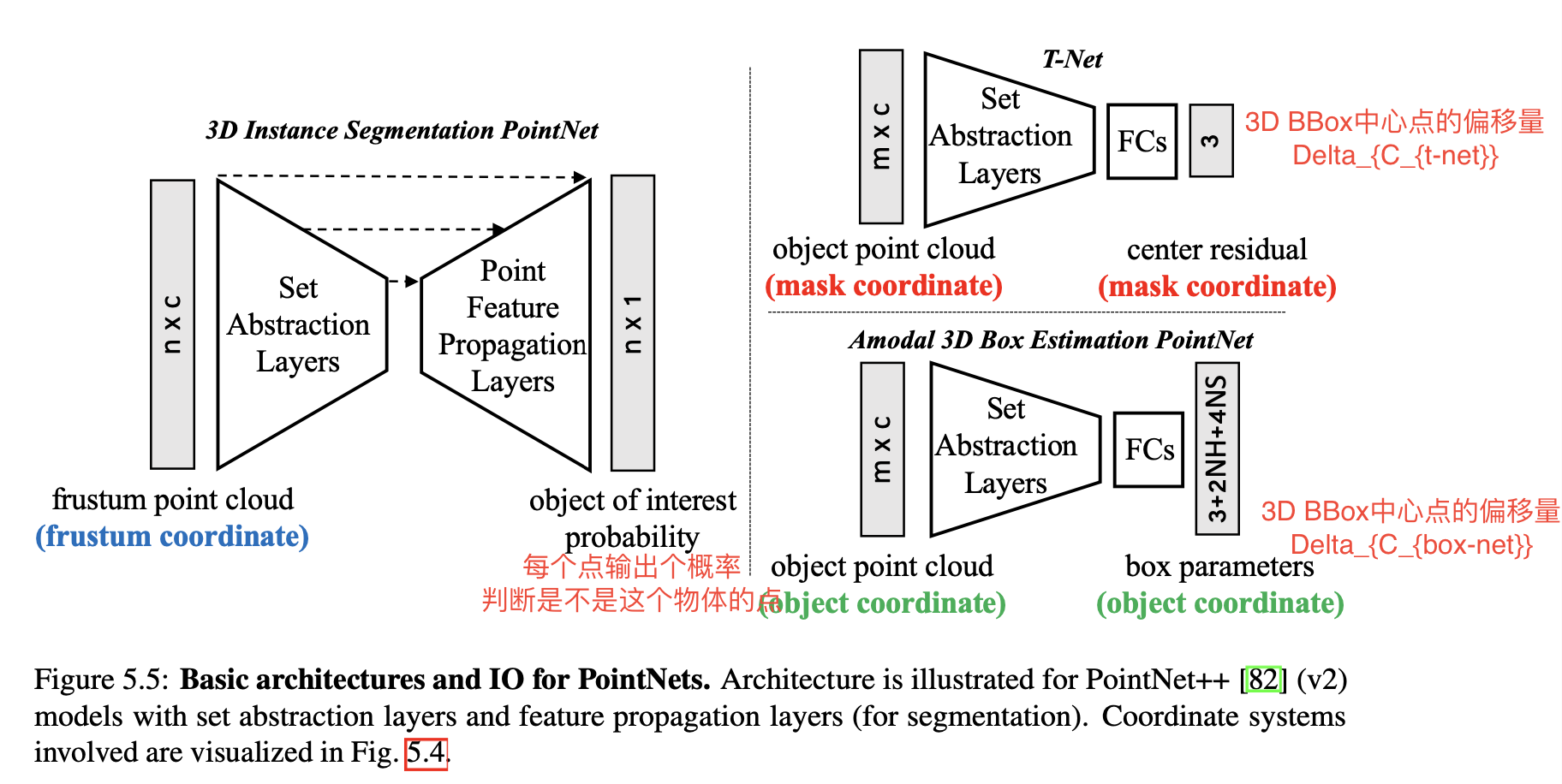
对上面这张图，需要做以下几点的解释说明：

• 上面涉及到了frustum coordinate，mask coordinate和object coordinate三个坐标系，它们之间的变换可以用下图表示。
  

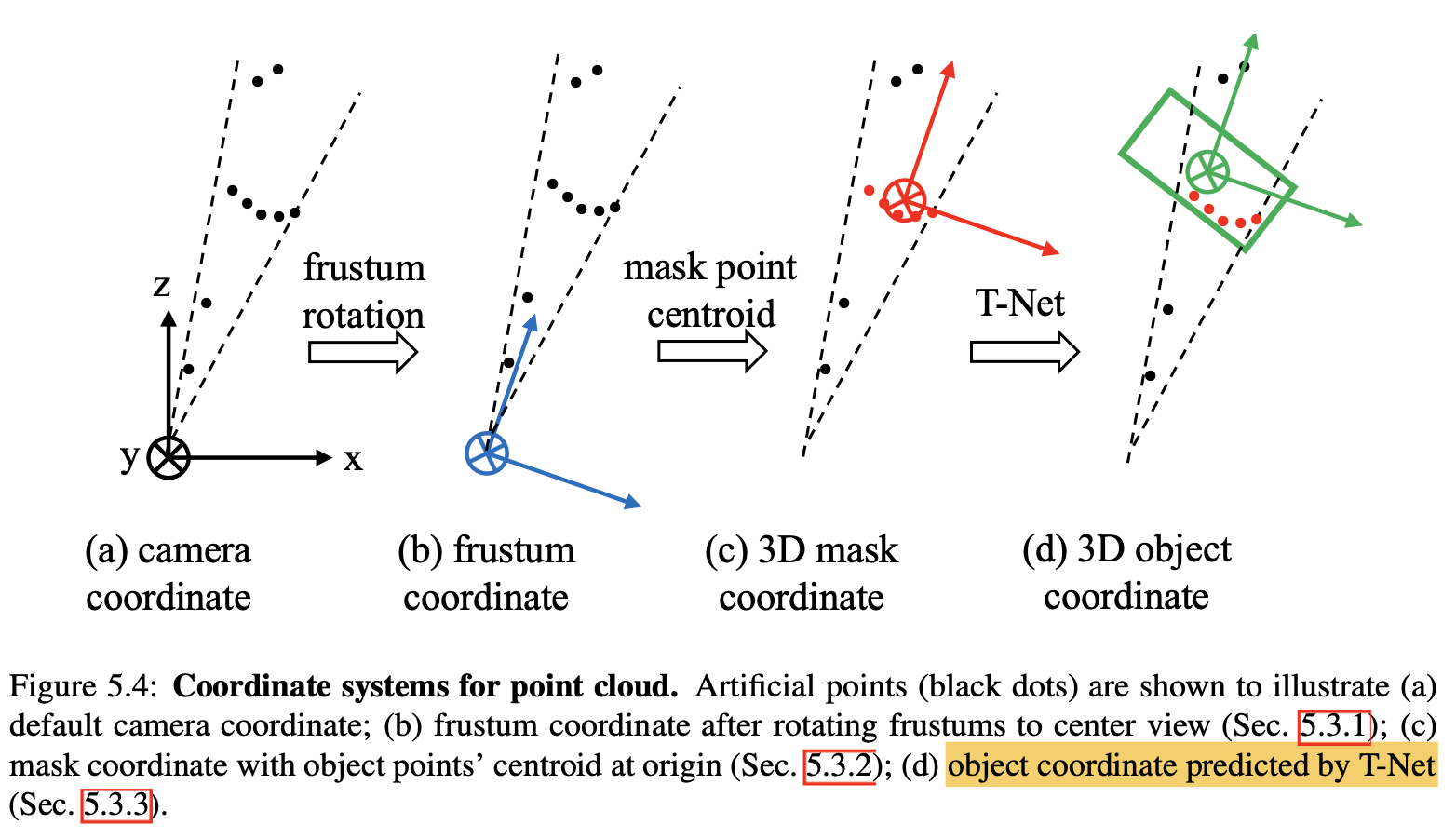
• Amodel 3D Box Estimation PointNet输出的位数为\(3+2NH+4NS \)。Frustum PointNet定义了NS个尺寸模板，并将heading angle \(\theta\)均匀的划分成了NH个angle bins。模型会预测：1）尺寸和heading anlge属于哪个模板(NH+NS位)；2）的residual(3NS + NH位)；3）中心点在object coordinate下的resiudal(3位)。
  

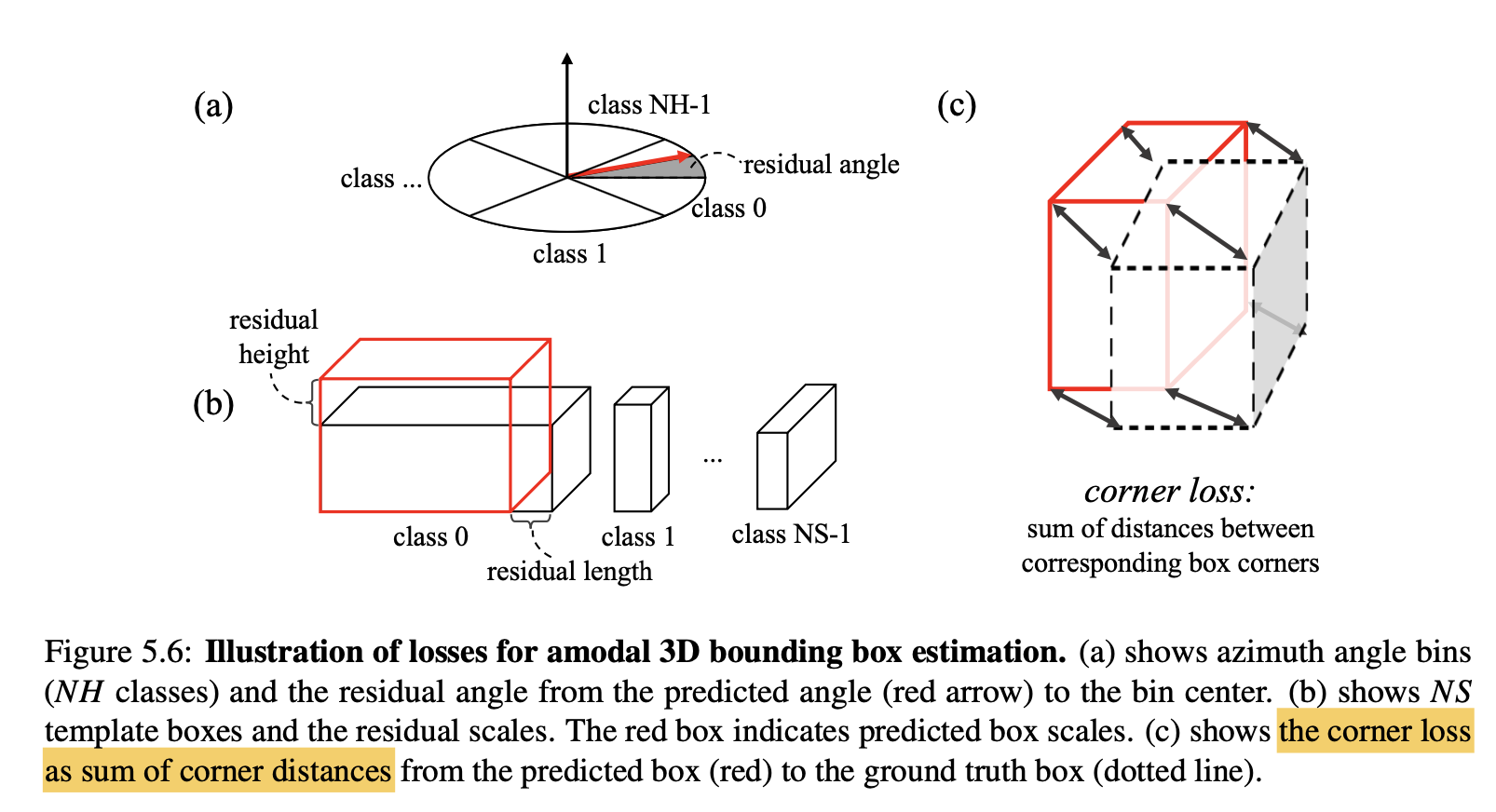
• 对于中心点\((c_x, c_y, c_z)\)的预测，论文描述地非常明白

We take a “residual” approach for box center estimation. The center residual predicted by the box estimation network is combined with the previous center residual from the T-Net and the masked points’ centroid to recover an absolute center
(\(C_{\text {pred }}=C_{\text {mask }}+\Delta C_{t-n e t}+\Delta C_{\text {box -net }}\)).

最后介绍Frustum PointNet的训练损失函数。完整的损失函数如下图所示：

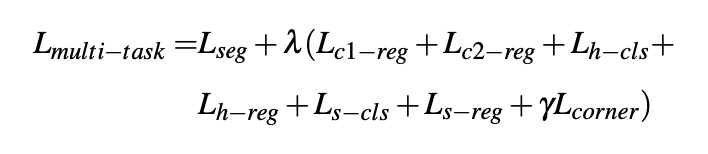
主要包含以下任务的损失：

• \(L_{seg}\)是3D Instance Segmentation PointNet的损失函数。
• \(L_{c1-reg}\)和\(L_{c2-reg}\)是和中心点相关的损失，前一个是T-Net的回归损失，后一个是Amodal 3D Box Estimation PointNet的回归损失。
• \(L_{h-cls}\)是heading angle的模板分类损失,\(L_{h-reg}\)是heading angle residual的回归损失。
• \(L_{s-cls}\)是3D BBox尺寸的模板分类损失，\(L_{s-reg}\)是尺寸的回归损失。
• \(L_{\text {corner }}=\sum_{i=1}^{N S} \sum_{j=1}^{N H} \delta_{i j} \min \left\{\sum_{k=1}^{8}\left\|P_{k}^{i j}-P_{k}^{*}\right\|, \sum_{i=1}^{8}\left\|P_{k}^{i j}-P_{k}^{* *}\right\|\right\}\)

  In essence, the corner loss is the sum of the distances between the eight corners of a predicted box and aground truth box. Since corner positions are jointly determined by center, size and heading, the corner loss is able to regularize the multi-task training for those parameter