Homography变换
0 具体做法
code: MaskTheFace
- 通过人脸关键点检测模型,可以得到特定点的像素坐标\(\{\vec{x_1}, \vec{x_2}, .., \vec{x_n}\}\)
- 找到口罩戴在脸上,特定点在口罩图像上的像素坐标\(\{\vec{y_1}, \vec{y_2}, ..., \vec{y_n}\}\)
- 通过homography变换,将口罩“贴”在人脸图像上
1 透视投影: Perspective Projection
介绍针孔相机模型前,我们需要对以下4个坐标系有所区分:
- 世界坐标系
- 相机坐标系
- 图像坐标系(and 归一化图像坐标系)
- 像素坐标系
世界坐标系—> 相机坐标系的转换,涉及到相机外参\(R\)和\(T\)
相机坐标系—> 图像坐标系的转换,涉及到相机内参\(f\)
图像坐标系—> 像素坐标系的转换,设计到相机内参\(s_x、s_y、s_\theta、o_x、o_y\)
1.1 针孔相机模型
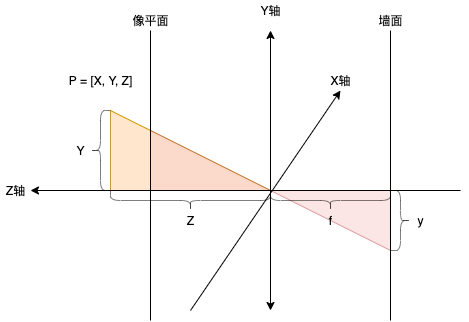
假设相机坐标系下点P的坐标是\([X, Y, Z]\),对应像平面上的点是\(p = [x, y]\),焦距为f,根据相似三角形可以得到从相机坐标系到图像坐标系的变换。(还没到像素坐标系)
\[ \begin{aligned}
\left\{\begin{array}{l}
\frac{f}{Z} =\frac{x}{X} \\
\frac{f}{Z}=\frac{y}{Y} \\
\end{array}\right.
\Rightarrow
\left\{\begin{array}{l}
x=f \cdot \frac{x}{Z} \\
y=f \cdot \frac{Y}{Z}
\end{array}\right.\\
\end{aligned}
\]
\[\begin{aligned}
Z\left[\begin{array}{l}
x \\
y \\
1
\end{array}\right] &=\left[\begin{array}{lll}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{array}\right]\left[\begin{array}{l}
X \\
Y \\
Z
\end{array}\right]
\end{aligned}
\]
用齐次坐标系表示,可以写成下面的形式:

1.2 各坐标系的变换——相机内参和外参
相机外参是相机的刚体运动,体现在世界坐标系到相机坐标系的坐标变换。相机内参体现在相机坐标系到图像坐标系到像素坐标系的变换。这部分内容也可参考TUM的PPT。


参考资料:
《Multiview Geometry Chapter 3——Perspective Projection》(TUM)
2 对极几何
根据两组2D点估计相机运动,可以使用对极几何求解
根据两组3D点估计相机运动,可以使用迭代最近点ICP求解
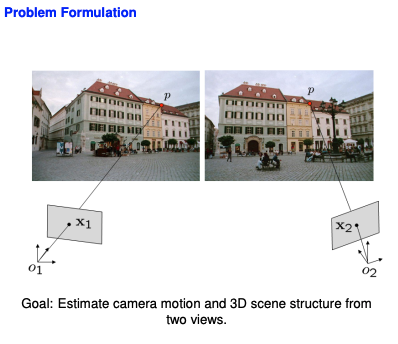

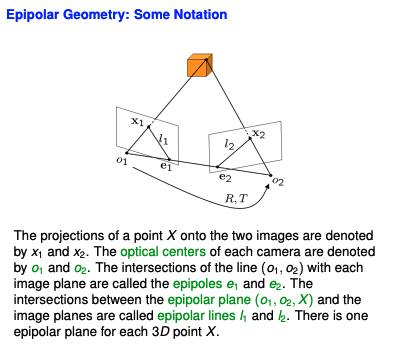
下面这张PPT需要注意两点:
- \(x_1\)和\(x_2\)是归一化像平面上的坐标。
- 对于向量\(u \in R^{3}\), 它的反称矩阵左乘一个向量,相当于它叉乘该向量。(右手法则)
\[\widehat{u}=\left(\begin{array}{ccc}
0 & -u_{3} & u_{2} \\
u_{3} & 0 & -u_{1} \\
-u_{2} & u_{1} & 0
\end{array}\right) \in \mathbb{R}^{3 \times 3}\]
\[\widehat{u} v=u \times v
\]


参考资料:
《Multiview Geometry Chapter 5——Reconstruction from Two Views: Linear Algorithms》(TUM)
3 单应性变换


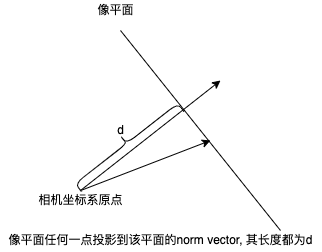
上面第一张PPT的第一个公式可以用下面这幅图来解释。
参考资料:
《Multiview Geometry Chapter 5——Reconstruction from Two Views: Linear Algorithms》(TUM)


