Modeling Filters and Whitening Filters

Colored and White Process

White Process

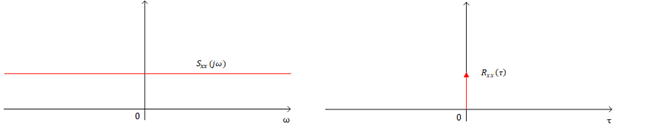
White Process，又称为White Noise（白噪声），其中white来源于白光，寓意着PSD的平坦分布，white noise指的就是在PSD上具有平坦分布（常数）的随机过程。PSD是auto-correlation的傅里叶变换，PSD上为常数意味着auto-correlation是一个位于零点上的脉冲函数。

回顾auto-correlation的定义：

$R_{xx}(\tau) = E\Big\{x(t+\tau)x(t)\Big\}$

Auto-correlation在零点上为脉冲，除此之外都是0，这表明了各个采样点之间是相互独立的，正是由于各采样点之间相互独立，才体现出了white noise的white这一特点。

理想的White noise要求PSD是一个常数，不过由于传输媒介以及有限的监测能力的关系，通常我们所得到的PSD都受限于某个带宽范围之内，因此如果一个process的PSD在监测范围（或者我们所感兴趣的频率范围）表现得平坦的话，就可以称该process为white noise。比如，如果一个音频的PSD在20~20000Hz内表现平坦的话，我们就可以称该音频为white noise。

i.i.d. process就是一个最简单white noise的例子。i.i.d. process中样本的PDF常见的有Uniform、Poisson、Gaussian等分布方式，如果PDF为Gaussian，则该process称为Gaussian white noise。

Colored Process

PSD表现得平坦的就是white noise，否则就是colored process。

Modeling Filter

输入为white process，输出为colored process的LTI系统被称为Modeling filter或者shaping filter。如果我们需要某个PSD为$S_{xx}(e^{j\Omega})$的process，可以通过设计一个LTI系统，并且对该系统输入mean为0的Bernoulli process（PSD为常数1）来得到，所设计的系统需要使得输出的process的PSD为$S_{xx}(e^{j\Omega})$。根据WSS Process在LTI系统中的性质，有

$\displaystyle{ H(e^{j\Omega}) = \sqrt{S_{xx}(e^{j\Omega})} }$

我们只需要对$H(e^{j\Omega})$进行傅里叶逆变换就可以得到所需LTI系统的脉冲响应$h[n]$。

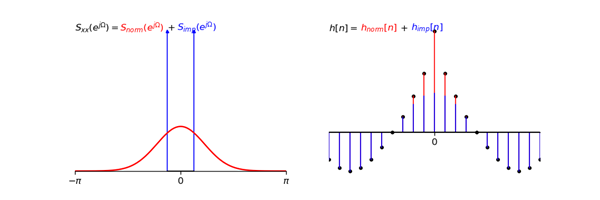
其中也可能会出现一些特殊情况，比如说所需要的process的PSD，即$S_{xx}(e^{j\Omega})$中包含脉冲，这些情况下，PSD可以表示为脉冲PSD与非脉冲PSD之和，由于傅里叶变换的线性性质，LTI系统的脉冲响应最终也可以表示为脉冲PSD的脉冲响应与非脉冲PSD的脉冲响应之和。非脉冲PSD可以按照上面的步骤求解，而脉冲PSD主要分为两种情况：