[离散时间信号处理学习笔记] 5. 离散时间信号与系统的频域表示

频率响应

从复指数输入引入频率响应

对于一个LTI系统，如果输入为$x[n] = e^{j\omega n},-\infty<n<\infty$，那么输出为

$\begin{align*}
y[n] &=  \sum_{k=-\infty}^{\infty}h[k]x[n-k] \\
&=\sum_{k=-\infty}^{\infty}h[k]e^{j\omega(n-k)}\\
&=\sum_{k=-\infty}^{\infty}h[k]e^{-j\omega k}e^{j\omega n}
\end{align*}$

式子当中，我们称$e^{j\omega n}$为该系统的特征函数，相应的特征值为

$H(e^{j\omega}) = \displaystyle{ \sum_{k=-\infty}^{\infty}h[k]e^{-j\omega k} }$

可以观察到特征值$H(e^{j\omega })$是与频率$\omega$相关的函数，因此特征值$H(e^{j\omega})$也被称为系统的频率响应。一般$H(e^{j\omega})$是复数，可以分为实部与虚部表示

$H(e^{j\omega}) = H_R(e^{j\omega}) + jH_I(e^{j\omega})$

也可以用幅度和相位表示

$H(e^{j\omega}) = |H(e^{j\omega})|e^{j\angle H(e^{j\omega)}}$

 

频率响应的广泛应用推论

这里我们可以做一个推论：如果信号能表示成由多个不同频率（$\omega_k$）的复指数的线性组合的形式

$x[n] = \displaystyle{ \sum_{k}a_k e^{j\omega_k n} }$

那么根据叠加原理，该信号经过线性时不变系统后得到相应的输出

$y[n] = \displaystyle{ \sum_{k}a_k H(e^{j\omega_k})e^{j\omega_k n} }$

 

频率响应的周期性

$\begin{align*}
H(e^{j(\omega+2\pi)})
&= \sum_{n=-\infty}^{\infty}h[n]e^{-j(\omega+2\pi)n} \\
&= \sum_{n=-\infty}^{\infty}h[n](e^{-j\omega n}e^{-j2\pi n})\\
&= \sum_{n=-\infty}^{\infty}h[n]e^{-j\omega n}\\
&= H(e^{j\omega})
\end{align*}$

频率响应$H(e^{j\omega})$作为一个变量为频率$\omega$的函数来说，它的周期为$2\pi$，只要确定了一个系统在区间$-\pi < \omega \leqslant \pi$上的频率响应，那么该系统在任意频率（$\omega$）的频率响应都能得到。其中靠近$0$处的频率就是低频，靠近$\pm \pi$处的频率就是高频。

 

常见系统的频率响应

理想延迟系统

定义：

$y[n] = x[n-n_d]$

当输入$x[n] = e^{j\omega n}$时，有

$y[n] = e^{j\omega (n-n_d)} = e^{-j\omega n_d}e^{j\omega n}$

因此这个理想延迟系统的频率响应为

$H(e^{j\omega}) = e^{-j\omega n_d}$

另外，用频率响应的定义式子也能求得该系统的频率响应

$\begin{align*}
H(e^{j\omega}) &=\sum_{k=-\infty}^{\infty}h[k]e^{-j\omega k} \\
&= \sum_{k=-\infty}^{\infty}\delta[k-n_d]e^{-j\omega k}\\
&= e^{-j\omega n_d}
\end{align*}$

根据欧拉公式可以求得频率响应的实部和虚部分别为

$\left \{ \begin{matrix}
H_R(e^{j\omega}) & = &cos(\omega n_d) \\
H_I(e^{j\omega}) & = &-sin(\omega n_d)
\end{matrix}\right .$

其幅度和相位是

$\left \{ \begin{matrix}
|H(e^{j\omega})| & = &1 \\
\angle H(e^{j\omega}) & = &-\omega n_d
\end{matrix}\right .$

 

单位脉冲响应为实数的LTI系统

如果$h[n]$为实数，则有

$\begin{align*}
H(e^{-j\omega})
&= \sum_{k=-\infty}^{\infty}h[k]e^{j\omega k} \\
&= \sum_{k=-\infty}^{\infty}h[k](cos(\omega k)+jsin(\omega k))\\
&= \underbrace{\sum_{k=-\infty}^{\infty}h[k]cos(\omega k)}_{H_R(e^{-j\omega})}+\underbrace{j\sum_{k=-\infty}^{\infty}h[k]sin(\omega k)}_{H_I(e^{-j\omega})} \quad h[k]\ is\ real\\
&= \underbrace{\sum_{k=-\infty}^{\infty}h[k]cos(-\omega k)}_{H_R(e^{j\omega})}-\underbrace{j\sum_{k=-\infty}^{\infty}h[k]sin(-\omega k)}_{H_I(e^{j\omega})} \quad h[k]\ is\ real\\
&=H^{*}(e^{j\omega})
\end{align*}$

 

LTI系统的正弦响应

如果一个LTI系统的输入为正弦的

$x[n] = Acos (\omega_0 + \phi) = \frac{A}{2}e^{j\phi}e^{j\omega_0 n} + \frac{A}{2}e^{-j\phi}e^{-j\omega_0 n}$

那么其输出为

$\begin{align*}
y[n]
&= \frac{A}{2}\{H(e^{j\omega_0})e^{j\phi}e^{j\omega_0 n}+H(e^{-j\omega_0})e^{-j\phi}e^{-j\omega_0 n} \} \\
&= \frac{A}{2}\{[H_R(e^{j \omega_0})+jH_I(e^{j\omega_0})]e^{j\phi}e^{j\omega_0 n}+[H_R(e^{j \omega_0})-jH_I(e^{j\omega_0})]e^{-j\phi}e^{-j\omega_0 n} \} \\ &\qquad h[n]\ is\ real\Rightarrow H(e^{-j\omega_0})=H^{*}(e^{j\omega_0})\\
&= \frac{A}{2}\{ H_R(e^{j\omega_0})(e^{j\phi}e^{j\omega_0 n}+e^{-j\phi}e^{-j\omega_0 n})+jH_I(e^{j\omega_0})(e^{j\phi}e^{j\omega_0 n}-e^{-j\phi}e^{-j\omega_0 n}) \} \\
&= \frac{A}{2} \{ 2H_R(e^{j\omega_0})cos(\omega_0 n + \phi) - 2H_I(e^{j\omega_0})sin(\omega_0 n + \phi) \} \\
&= A \{ H_R(e^{j\omega_0})cos(\omega_0 n + \phi) - H_I(e^{j\omega_0})sin(\omega_0 n + \phi) \} \\
&= A\{ |H(e^{j\omega_0})|cos(\theta)cos(\omega_0 n +\phi)-|H(e^{j\omega_0})|sin(\theta)sin(\omega_0 n +\phi)\} \quad letting\ \theta=\angle H(e^{j\omega_0})\\
&= A |H(e^{j\omega_0})| cos(\omega_0 n +\phi+\theta)
\end{align*}$

如果当前的LTI系统为理想延迟系统，在前面已经得到其幅度与相位$|H(e^{j\omega_0})|=1,\theta = –\omega_0 n_d$，因此

$\begin{align*}
y[n]
&= Acos(\omega_0 n +\phi-\omega_0 n_d)\\
&= Acos[\omega_0(n-n_d)+\phi]
\end{align*}$

这与直接利用理想延迟系统的定义得到的结果是一致的。

 

滑动平均系统

单位脉冲响应为

$h[n]=\left\{\begin{matrix}
\frac{1}{M_1+M_2+1} ,& -M\leqslant n\leqslant M_2 \\
0, &else
\end{matrix}\right .$

因此频率响应为

$H(e^{j\omega}) = \frac{1}{M_1+M_2+1}\displaystyle{\sum_{n=-M_1}^{M_2}e^{-j\omega n}}$

对于因果滑动平滑系统，$M_1 = 0$，即

$H(e^{j\omega}) = \frac{1}{M_2+1}\displaystyle{ \sum_{n=0}^{M_2}e^{-j\omega n} }$

运用几何级数求和公式可以得到

$\begin{align*}
H(e^{j\omega}) & = \frac{1}{M_2+1}\sum_{n=0}^{M_2}e^{-j\omega n}\\
&= \frac{1}{M_2+1}\left( \frac{1-e^{-j\omega(M_2+1)}}{1-e^{-j\omega}} \right ) \\
&= \frac{1}{M_2+1}\left( \frac{(e^{j\omega(M_2+1)/2}-e^{-j\omega(M_2+1)/2})e^{-j\omega(M_2+1)/2}}{(e^{j\omega/2}-e^{-j\omega/2})e^{-j\omega/2}} \right )\\
&= \frac{1}{M_2+1}\left(\frac{sin[\omega(M_2+1)/2]}{sin\omega/2}e^{-j\omega M_2/2} \right )
\end{align*}$

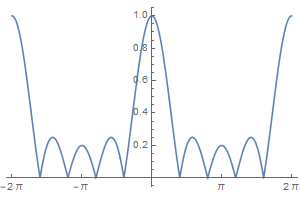
当$M_2=4$时，频率响应的模和相位如下

    

频率响应的模与相位都会随着频率$\omega$的变化而变化，其中从模的图形中能看出在$\pi$（高频）附近的值明显比$0$处（低频）小，也就是起到了截断高频、通过低频的作用，算是一个较为粗糙的低通滤波器，这一点与滑动平均系统的特性是一致的。

 

 

因果LTI系统的频率响应

前面的文章已经说过，因果LTI系统有一些比较重要的特点：

• 输出$y[n]$不能使用超前的输入$x[n+m],m>0$来计算
• 系统的单位脉冲响应$h[n]=0,for \ n<0$
• 在未进行输入之前不会有输出（初始松弛条件）

 

稳态响应与暂态响应的定义

现考虑在$n=0$时刻开始向一个因果LTI系统输入复指数信号，

$u[x] = e^{j\omega n}u[n]$

那么输出为

$y[n]=\left \{\begin{matrix}
0, &n<0 \\
\left( \displaystyle{\sum_{k=0}^{n}h[k]e^{-j\omega k}}\right )e^{j\omega n}, &n \geqslant 0
\end{matrix} \right .$

由于在$n<0$时$y[n]$为$0$，因此这里只考虑$n\geqslant 0$时的输出

$\begin{align*}
y[n]&=\left( \sum_{k=0}^{n}h[k]e^{-j\omega k}\right )e^{j\omega n} \\
&=\left(\sum_{k=0}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n}-\left(\sum_{k=n+1}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n}\\
&=\left(\sum_{k=-\infty}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n} - \left(\sum_{k=n+1}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n} \quad h[k]=0,k<0\\
&=H(e^{j\omega})e^{j\omega n} - \left(\sum_{k=n+1}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n}\\
\end{align*}$

可见输出由两部分组成，$y[n] = y_{ss}[n]+y_t[n]$，其中

$y_{ss}[n]=H(e^{j\omega})e^{j\omega n}$

这部分被称为稳态响应（steady-state response），也就是当系统的输入为$e^{j\omega n}$时的输出。而第二部分

$y_t[n] =  \displaystyle{ - \left(\sum_{k=n+1}^{\infty}h[k]e^{-j\omega k} \right )e^{j\omega n}}$

就是系统输出偏离特征函数（即$e^{j\omega n}$）的输出的量。这一部分被称为暂态响应（transient response）。

 

稳态响应与暂态响应在输出过程中的变化

前面已经说过稳态响应是当系统输入为$e^{j\omega n}$时的输出，那么暂态响应是否也有什么含义呢，我们先来对暂态响应做进一步推导

$\begin{align*}
y_t[n] &=   \sum_{k=n+1}^{\infty}h[k]e^{-j\omega k}e^{j\omega n} \\
& = \sum_{m=-\infty}^{-n-1}h[-m]e^{j\omega m}e^{j\omega n} \quad letting\ m=-k\\
& = \sum_{p=-\infty}^{-1}h[n-p]e^{j\omega (p-n)}e^{j\omega n}\quad letting\ p=m+n\\
& = \sum_{p=-\infty}^{-1}h[n-p]e^{j\omega p}
\end{align*}$

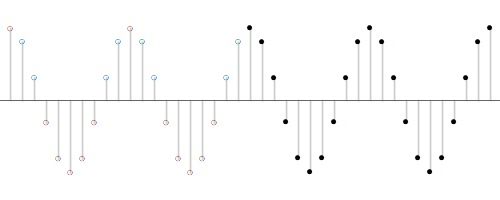
下图所示的是频率为$\omega = 2\pi/10$的复指数信号的实部，图中实心点的是系统的实际输入，空心点的是丢失的输入（这样的输入代表了从$n=0$时开始对因果LTI系统进行输入）。

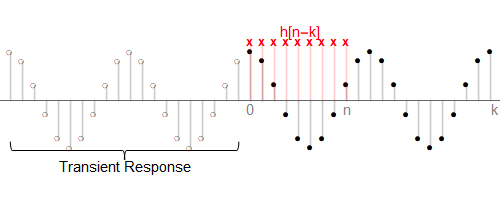
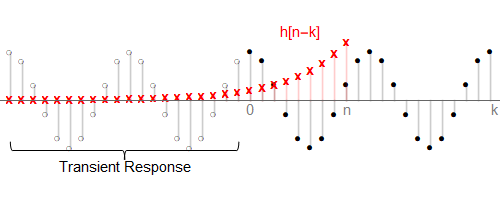
按照上面式子推导出来的结果，在某个时刻$n$的暂态响应，选取的是开始输入之前的那部份输入序列。

当$h[n]$长度有限时，暂态响应会在$h[n-k]$与$x[n]$完全相交后变为0

当$h[n]$长度无限时，如果是稳定的系统，则在$n\to \infty$时有$h[n]\to 0$，暂态响应也会随着$n$的增大而逐渐变小，在$n\to\infty$时有$y_t[n]\to 0$。

这也说明了随着$n$的增大，暂态响应的影响会越来越小，稳态响应的影响则越来越大。