高维傅里叶变换的移位定理
在一维傅里叶变换的移位定理时,有
f(t)↔F(s)
f(t−b)↔e−2πisbF(s)
在二维傅里叶变换的移位定理时,有两个变量,可分别对它们进行移位,
f(x1,x2)↔F(ξ1,ξ2)
f(x1−b1,x2−b2)↔?
二维的移位对应的傅里叶变换是什么呢?下面进行计算
∫∞−∞∫∞−∞e−2πi(x1ξ1+x2ξ2)f(x1−b1,x2−b2)dx1dx2=∫∞−∞∫∞−∞e−2πi((u1+b1)ξ1+(u2+b2)ξ2)f(u1,u2)du1du2letting u1=x1−b1,u2=x2−b2=∫∞−∞∫∞−∞e−2πi(b1ξ1+b2ξ2)e−2πi(u1ξ1+u2ξ2)f(u1,u2)du1du2=e−2πi(b1ξ1+b2ξ2)∫∞−∞∫∞−∞e−2πi(u1ξ1+u2ξ2)f(u1,u2)du1du2=e−2πi(b1ξ1+b2ξ2)F(ξ1,ξ2)
即二维移位定理可以表示为
f(x1−b1,x2−b2)↔e−2πi(b1ξ1+b2ξ2)F(ξ1,ξ2)
表示成向量形式
f(x––)↔F(ξ–)
f(x––−b–)↔e−2πiξ–⋅b–F(ξ–)
这个向量形式也可以推广到n维傅里叶变换的移位定理。
高维傅里叶变换缩放定理
独立变量缩放
在一维傅里叶变换的缩放定理时,有
f(t)↔F(s)
f(at)↔1|a|F(sa)
通过这个式子,我们知道时域与频域的缩放是互反的,不可能在时域与频域上同时压缩或同时扩展。
在二维傅里叶变换的缩放定理时,有
f(x1,x2)↔F(ξ1,ξ2)
f(a1x1,a2x2)↔1|a1||a2|F(ξ1a1,ξ2a2)
在二维傅里叶变换的公式中通过变量替换就能得到上述结果,这里不进行具体的推导。
混合变量缩放(矩阵乘法)
不过缩放并不限于x1→a1x1,x2→a2x2这种各个变量独立缩放的形式,更一般的情况会表示为矩阵的乘法,即
[x1x2]→[abcd][x1x2]=[ax1+bx2cx1+dx2]
这种缩放也可以推广到n维傅里叶变换。
用向量形式来表示
x––→Ax––
f(x––)→f(Ax––)
需要注意的是,这里的矩阵A是非奇异的,即不能使得x––降阶(不能消去x––中的某一项).
它的傅里叶变换为
F(f(Ax––))=∫Rne−2πi(x––⋅ξ–)f(Ax––)dx––=∫Rne−2πi(A−1u––⋅ξ–)f(u––)d(A−1u––)letting u––=Ax––=∫Rne−2πi(u––⋅(A−1)Tξ–)f(u––)1|detA|du––please review linear algebra=∫Rne−2πi(u––⋅A−Tξ–)f(u––)1|detA|du––letting A−T=(A−1)T=1|detA|∫Rne−2πi(u––⋅A−Tξ–)f(u––)du––=1|detA|Ff(A−Tξ–)
即
f(x––)↔F(ξ–)
f(Ax––)↔1|detA|F(A−Tξ–)
在一维傅里叶变换的缩放定理时,只有一个变量,因此我们用倒数就能表达出时域与频域间的缩放关系,但是在高维傅里叶变换,有多个变量,因此缩放就变得更为自由,我们为了表示高维的缩放引入了矩阵,傅里叶的缩放关系也从倒数变成了矩阵的逆转置A−T。
下面是关于高维傅里叶缩放定理的两个例子
例一
我们前面所说到的独立变量的缩放
f(a1x1,a2x2)=f(Ax––)
其中A=[a100a2]
f(Ax––)↔1|detA|F(A−Tξ–)=1|a1a2−0|F([1a1001a2][ξ1ξ2])=1|a1||a2|F(ξ1a1,ξ2a2)
例二
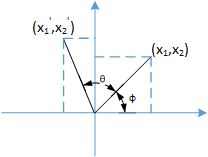
矩阵为A=[cosθ−sinθsinθcosθ],那么Ax––=[x1cosθ−x2sinθx1sinθ+x2cosθ]
假设原始的变量为(x1,x2),用矩阵A进行缩放后的变量为(x′1,x′2),引入极坐标系,他们间有如下关系
x1=rcosφx2=rsinφ
x′1=x1cosθ−x2sinθ=rcosφcosθ−rsinφsinθ=rcos(φ+θ)
x′2=x1sinθ+x2cosθ=rcosφsinθ+rsinφcosθ=rsin(φ+θ)
那么这个矩阵就代表了f(x1,x2)在空域的x1,x2平面上进行了角度为θ的旋转。
它的傅里叶变换为
1|detA|F(A−Tξ–)=1|cosθcosθ−(−sinθ)sinθ|F((A−1)Tξ–)=F((AT)Tξ–)AAT=[cosθ−sinθsinθcosθ][cosθsinθ−sinθcosθ]=[1001]=I ⇒AT=A−1=F(Aξ–)
即,当A=[cosθ−sinθsinθcosθ],有
f(Ax––)↔F(Aξ–)
这表明空间坐标系旋转对应着频率坐标系的相同角度的旋转。
从二维图像上去思考的话,f(Ax––)相当于一幅被旋转了的图像,F(Aξ–)就是该图像的频谱进行了相应的旋转而已,并没有本质上的改变。
高维δ函数
高维δ函数与一维的δ函数有着相同性质
<δ,φ>=φ(0–)=φ(0,0,…,0n)
移位的脉冲函数δb–=δ(x––−b–)
<δb–,φ>=φ(b–)=φ(b1,b2,…,bn)
傅里叶变换
Fδ=1
Fδb–=e−2πi(b–⋅ξ–)
δ的取样特性
fδ=f(0–)δ
fδb–=f(b–)δb–
δ的缩放特性
我们以前讲过一维的情况
一维:
δ(ax)=1|a|δ(x)
n维:
δ(Ax––)=1|detA|δ(x––)




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架