[傅里叶变换及其应用学习笔记] 二十. 离散傅里叶变换的定义

 

DFT

离散傅里叶变换有定义如下

有离散信号$\underline{f}=\left( \underline{f}[0],\underline{f}[1],…,\underline{f}[N-1] \right)$，它的DFT是离散信号$\underline{\mathcal{F}f}\left( \underline{\mathcal{F}f}[0],\underline{\mathcal{F}f}[1],…,\underline{\mathcal{F}f}[N-1] \right)$

$\underline{\mathcal{F}f}[m] = \displaystyle{ \sum_{k=0}^{N-1}\underline{f}[k]e^{-2\pi ik\frac{m}{N}} }$

 

 

时域和频域的倒数关系

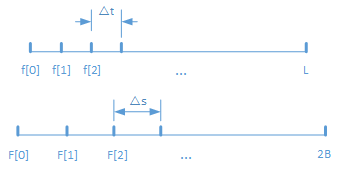
我们回到连续信号，从头开始推导这一关系。

设有一连续信号在时域与频域同时受限，时域与频域都有$N$个采样点（上节课已推导过，时域与频域抽样点的数目是一样的），时域采样间隔为$\Delta t$，频域采样间隔为$\Delta s$，根据不同的$\Delta t$与$\Delta s$可以采集到不同的$\underline{f}$，与$\underline{\mathcal{F}f}$。

 

有$N\Delta t = L$，$L$为时间上的限制；$N\Delta s = 2B$，$2B$为带宽限制。

$\Delta t \Delta s = \frac{L}{N}\cdot \frac{2B}{N} = \frac{2BL}{N^2} = \frac{N}{N^2} = \frac{1}{N}$

 

因此有

$\Delta t \Delta s = \frac{1}{N}$

 

时域的采样间隔和频域的采样间隔会根据抽样点数成倒数关系（reciprocity relationship）。这该关系对于进行DFT很有现实意义。如：当我们确定好时域的采样间隔$\Delta t$与抽样点数$N$时，频域的采样间隔$\Delta s$就被固定了，即频域分辨率是由时域所做的选择而确定的。（The resolution in frequency is determined by the choices you make in time.）

 

 

引入新符号$\underline{\omega}$

令$\underline{\omega}$为离散的复指数信号（或为复指数向量），且

$\underline{\omega} = \left( 1,e^{2\pi i\frac{1}{N}},e^{2\pi i\frac{2}{N}},…,e^{2\pi i\frac{N-1}{N}} \right)$

$\underline{\omega}[m] = e^{2\pi i\frac{m}{N}}$

 

那么对$\underline{\omega}$进行幂运算，有

$\underline{\omega}^n = \left(1,e^{2\pi i\frac{n}{N}},e^{2\pi i\frac{2n}{N}},…,e^{2\pi i\frac{n(N-1)}{N}} \right)$

$\underline{\omega}^{-n} = \left(1,e^{-2\pi i\frac{-n}{N}},e^{-2\pi i\frac{2n}{N}},…,e^{-2\pi i\frac{n(N-1)}{N}} \right)$

$\underline{\omega}^{-n}[m] = e^{-2\pi i\frac{mn}{N}}$

 

把它代入到DFT中，有

$\underline{\mathcal{F}f}[m] = \displaystyle{ \sum_{n=0}^{N-1}\underline{f}[n]e^{-2\pi i\frac{mn}{N}} = \sum_{n=0}^{N-1}\underline{f}[n] \underline{\omega}^{-n}[m] }$

 

隐藏序号$m$，则有

$\underline{ \mathcal{F}f} = \displaystyle{ \sum_{n=0}^{N-1}\underline{f}[n]\underline{\omega}^{-n} }$

 

 

DFT特性

1) 输入和输出的周期性（The periodicity of the inputs and outputs）。

DFT的定义迫使我们把输入$\underline{f}$与输出$\underline{\mathcal{F}f}$不仅当作定义在$0$到$N-1$整数上的，并且是周期为$N$的周期离散函数，这是因为$\underline{\omega}$，它的离散复指数应该是一个周期为$N$的周期离散函数。我们将在下节课讲述这一特性。

（The definition of DFT compels you to regard the input $\underline{f}$ output $\underline{\mathcal{F}f}$，its discrete Fourier transform as not just defined on the integers from $0$ to $N-1$，but as periodic discrete signals of period $N$. This is so because $\underline{\omega}$ itself，its discrete complex exponential should be – is naturally a periodic discrete signal of period $N$.）

 

2) 离散复指数的正交性（Orthogonality of the discrete complex exponentials）

回顾一下上述的离散复指数信号$\underline{\omega}$，

$\underline{\omega} = \left( 1,e^{2\pi i\frac{1}{N}},e^{2\pi i\frac{2}{N}},…,e^{2\pi i\frac{N-1}{N}} \right)$

$\underline{\omega}^k = \left(1,e^{2\pi i\frac{k}{N}},e^{2\pi i\frac{2k}{N}},…,e^{2\pi i\frac{k(N-1)}{N}} \right)$

 

如果$k\neq l$，则有$\underline{\omega}^k$与$\underline{\omega}^l$是正交的。

这里不把$\underline{\omega}$当作离散信号，而是把它当作$N$维向量，我们在讨论傅里叶级数复指数的时候引入了正交，这里可谓它的离散版本，即

如果$k\neq l$，

$\begin{align*} \underline{\omega}^k\cdot \underline{\omega}^l &=\sum_{n=0}^{N-1}\underline{\omega}^k[n]\overline{\underline{\omega}^l[n]}\\ &=\sum_{n=0}^{N-1}e^{2\pi i\frac{kn}{N}}\overline{e^{2\pi i\frac{ln}{N}}}\\ &=\sum_{n=0}^{N-1}e^{2\pi i\frac{kn}{N}}e^{-2\pi i\frac{ln}{N}}\\ &=\sum_{n=0}^{N-1}\left( e^{2\pi i\frac{k-l}{N}} \right)^n\\ &=\frac{1- \left( e^{2\pi i\frac{k-l}{N}} \right)^N }{1-e^{2\pi i\frac{k-l}{N}}} \qquad(Geometric\ Series,\quad because\ k\neq l,\ this\ fraction\ is\ ok)\\ &=\frac{1-e^{2\pi i(k-l)}}{1-e^{2\pi i\frac{k-l}{N}}}\\ &=\frac{1-(isin(2\pi(k-l))+cos(2\pi(k-l)))}{1-e^{2\pi i\frac{k-l}{N}}} \qquad (Eular\ formula)\\ &=\frac{1-(0+1)}{1-e^{2\pi i\frac{k-l}{N}}}\\ &=0 \end{align*}$

 

如果$k = l$，

$\begin{align*} \underline{\omega}^k\cdot \underline{\omega}^l &=\sum_{n=0}^{N-1}\underline{\omega}^k[n]\overline{\underline{\omega}^l[n]}\\ &=\sum_{n=0}^{N-1}\left( e^{2\pi i\frac{k-l}{N}} \right)^n\\ &=\sum_{n=0}^{N-1}(e^0)^n \qquad(k=l)\\ &=N \end{align*}$

 

因此

$\underline{\omega}^k\cdot \underline{\omega}^l = \begin{cases} 0 & \text{,} k\neq l \\ N & \text{,} k=l \end{cases}$

 

当$l\neq k$时$\underline{\omega}^k$与$\underline{\omega}^l$是正交的，但是它们并不是标准正交，因为$\left\| \underline{\omega}^k \right\| = \underline{\omega}^k\cdot \underline{\omega}^k = N$而不是等于$1$，因此有时为了归一为标准正交向量，会把$N$引入到$\underline{\omega}$中。

 

 

IDFT

离散傅里叶逆变换有公式如下

$\underline{\mathcal{F}^{-1}f}[m] = \displaystyle{ \frac{1}{N}\sum_{n=0}^{N-1}\underline{f}[n]e^{2\pi i \frac{mn}{N}} = \frac{1}{N}\sum_{n=0}^{N-1}\underline{f}[n]\underline{\omega}^n[m] }$

 

省略序号$m$，则

$\underline{\mathcal{F}^{-1}f} = \displaystyle{ \frac{1}{N}\sum_{n=0}^{N-1}\underline{f}[n]\underline{\omega}^n }$

 

IDFT的职责是把进行了DFT的离散信号复原，即

$\underline{\mathcal{F}^{-1}\mathcal{F}f} = \underline{f}$

$\underline{\mathcal{F}^{-1}\mathcal{F}f}[m] = \underline{f}[m]$

 

证明过程需要用到$\underline{\omega}$的正交性质

$\begin{align*} \underline{\mathcal{F}^{-1}\mathcal{F}f}[m] &=\frac{1}{N}\sum_{n=0}^{N-1}\underline{\mathcal{F}f}[n]e^{2\pi i\frac{mn}{N}}\\ &=\frac{1}{N}\sum_{n=0}^{N-1}\left( \sum_{k=0}^{N-1}\underline{f}[k]e^{-2\pi i\frac{kn}{N}} \right)e^{2\pi i\frac{mn}{N}}\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\underline{f}[k]\left( \sum_{n=0}^{N-1}e^{-2\pi i\frac{kn}{N}}e^{2\pi i\frac{mn}{N}} \right)\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\underline{f}[k]\left( \underline{\omega}^k \cdot \underline{\omega}^m \right)\\ &=\frac{1}{N}\sum_{k=0}^{N-1}f[k]\cdot N \qquad \left( \underline{\omega}^k\cdot \underline{\omega}^m = \begin{cases} 0 & \text{,} k\neq m \\ N & \text{,} k=m \end{cases} \right)\\ &=f[m] \end{align*}$