[傅里叶变换及其应用学习笔记] 十五. 傅里叶变换在衍射上的应用
这份是本人的学习笔记，课程为网易公开课上的斯坦福大学公开课：傅里叶变换及其应用。
光的衍射（Diffraction）
光在传播过程中，遇到障碍物或小孔（窄缝）时，它有离开直线路径绕到障碍物阴影里去的现象，这种现象称为光的衍射。衍射会产生明暗条纹或光环。
衍射的形成有三个要素：
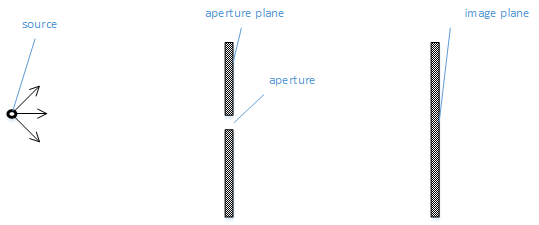
1. 光源（source）
2. 上面分布着小孔的衍射屏（aperture plane），光线只能通过小孔穿透到另一侧
3. 接收小孔传播过来的光线，并在上面形成图形的的接收屏（image plane）
衍射屏与接收屏的距离决定了有两种衍射
1. 衍射屏与接收屏的距离相比光波长较近，称为近场衍射（near-field），又成为菲涅耳衍射（Frenel diffraction）
2. 衍射屏与接收屏的距离相比光波长较远，称为远场衍射（far-field），又称为夫琅禾费衍射（Fraunhoffer diffraction）
我们平常所做的衍射实验还有一个附加条件：光源需要离衍射屏足够远，使得光可以平行经过衍射屏上的小孔，并且光波在衍射平面上有相同的相位。
光的数学表示
我们这里只研究光的波动性。因此假设光是震荡的电磁场，并且是单色光（单一频率）。
在衍射屏上有光波表示为（波的复数表示形式）
$Ee^{2\pi i\nu t}$
其中$E$表示电场强度，$\nu$表示频率，$t$为时间，表明光波随时间波动。
接收屏上的光波表示
要求解这个问题需要用到惠更斯原理（Huyghens' Principle）。惠更斯原理讲的是，衍射屏上的每个小孔，都可以视为一个新的光源。
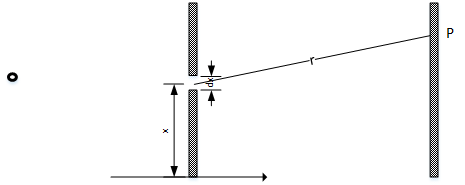
如上图，则通过$dx$的光波记为
$E_0e^{2\pi i\nu t}dx$
现要求$P$点处光波的变化。光波在$P$点的变化有幅度与相位的变化，我们这里分析的是相位变化，因此忽略幅度变化。
相位与光传播的距离$r$以及光的波长$\lambda$相关。小孔$x$与$P$点间有$\frac{r}{\lambda}$个光波，因此相位（弧度）的变化为$\frac{2\pi r}{\lambda}$。因此经由$x$到$P$点的光波为
$dE = E_0e^{2\pi i\nu t}e^{2\pi i\frac{r}{\lambda}}$
因此，经过整个衍射屏后传播到$P$点的总光波为
$E=\displaystyle{\int_{aperture}E_0e^{2\pi i\nu t}e^{2\pi i\frac{r}{\lambda}}dx }$
与$x$相关的部分只有$r$，因此
$E=\displaystyle{E_0e^{2\pi i\nu t}\int_ {aperture}e^{2\pi i \frac{r}{\lambda}}dx }$
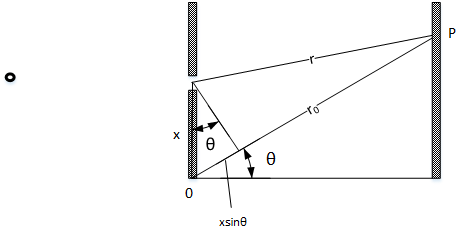
现引入夫琅禾费近似公式
假设$r\gg x$，则
$r=r_0-xsin\theta$
把该等式代入上述光波$E$的式子，得
$\begin{align*}E
&=E_0e^{2\pi i\nu t}\int_{aperture}e^{2\pi i\frac{1}{\lambda}(r_0-xsin\theta)}dx\\
&=E_0e^{2\pi i\nu t}e^{2\pi i\frac{r_0}{\lambda}}\int_{aperture}e^{-2\pi i\frac{xsin\theta}{\lambda}}dx
\end{align*}$
由于我们只关心相位的相关部分，也就是积分内的相关部分，因此可以写成
$E \propto \displaystyle{\int_{aperture}e^{-2\pi ix\frac{sin\theta}{\lambda}}dx}$
令$p=\frac{sin\theta}{\lambda}$，
$E \propto \displaystyle{\int_{aperture}e^{-2\pi ixp}dx}$
对于衍射屏上的小孔，我们可以用孔径函数$A(x)$来记录
$A(x)=\begin{cases}
1 & \text{ , } x\in aperture \\
0 & \text{ , } otherwise
\end{cases}$
只有小孔才能使光波穿过，其余地方都不透光，即
$E\propto \displaystyle{\int_{-\infty}^{\infty}A(x)e^{-2\pi ipx}dx }$
我们看到，等式右边是一个傅里叶变换，即
$E\propto \mathcal{F}A(p)\quad ,\quad p=\frac{sin\theta}{\lambda}$
结论：
- 光的强度是孔径函数傅里叶变换的幅值（Intensity of the light is the magnitude of the Fourier Transform of aperture function）
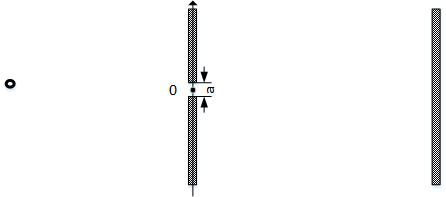
单缝衍射
单缝衍射的截面的孔径函数是一个$\Pi$函数
$A(x)=\Pi_a(x)$
那么其衍射图像的截面为
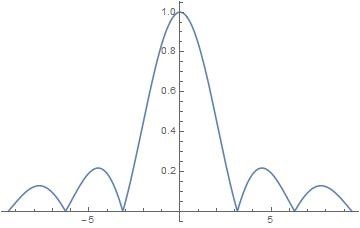
$\mathcal{F}A(x)=asinc\left( \frac{asin\theta}{\lambda} \right) \quad,\quad p=\frac{sin\theta}{\lambda}$
我们肉眼观察到的光强度是其绝对值
$|\mathcal{F}A(x)|=\left| asinc\left( \frac{asin\theta}{\lambda} \right)\right| $
如果光不是从小孔射进，而是一个点（point），即点光源，而接收屏离衍射屏足够远，那么有如下分析：在点上射出的光源用$\delta$表示，其在接收屏的光为$\mathcal{F}\delta=1$，即光会均匀照亮接收屏。
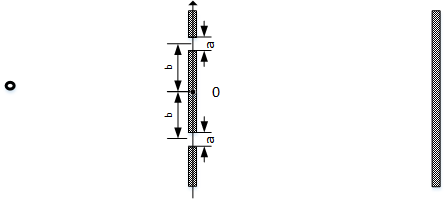
杨氏双缝实验（Young's double slits）
$A(x) = \Pi_a(x-\frac{b}{2})+\Pi_a(x+\frac{b}{2})$
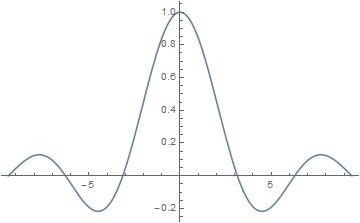
$\mathcal{F}A(x) = a(sinap)2cos(\pi bp)\quad,\quad p=\frac{2\pi \theta}{\lambda}$
