[傅里叶变换及其应用学习笔记] 一. 预备知识
这份是本人的学习笔记，课程为网易公开课上的斯坦福大学公开课：傅里叶变换及其应用。
本课程学习路线
从傅里叶级数开始，后续过渡到傅里叶变换。
扼要描述
- 傅里叶级数（fourier series），几乎等同于周期性现象的学习。
- 傅里叶变换（fourier transform），可作为傅里叶级数的极限情况，是对非周期性现象的数学分析。
两者间的共同点
- 分析（analysis），分解一个信号（函数），把它拆分成一系列组成部分，并希望这些组成部分比复杂的原始信号（函数）简单。
- 合成（synthesis），把基本的组成部分重组成信号本身。
分析与合成总是成对出现，我们把复杂的信号分离成简单信号，然后进行我们需要的处理，最后再组合成原始信号。
线性运算
傅里叶分析与合成是由线性运算完成的，线性运算包含有积分和序列。傅里叶分析经常被认为是线性分析的一部分。
周期性现象
周期性现象有两种：
- 时间上的周期性
- 空间上的周期性
对称性与周期性的关系
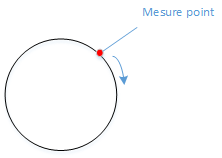
例：圆环上的热量分布
在这个例子里面认为温度不受时间影响，温度与圆环的位置有关。
我们从圆环上的某点A测试圆环的温度，然后沿着顺时针方向一直测试，最终又会回到A点继续顺时针测试温度，这样我们就能得到呈现周期性的温度值。
从上述测试我们可以得到初步结果：
目标（圆环）重复--->目标对称--->相关值的周期性
这里引出一个论点：傅里叶分析通常与具有对称性问题相关
周期性
- 在时域上，用频率（frequency）表达。
- 在空域上，用周期（period）表达。
两者有时会一起出现，如波动（wave motion）。
一个规则的波动含有波长（$\lambda$）与频率（$\vartheta$）属性。
- 波长，即某一时间点，一个完整波扰动的长度。
- 频率，1秒内出现波扰动的次数。
两者有以下关系：
设波的传播速度为$v$，有
$v = \lambda \cdot \vartheta $
波长与频率成反比例关系。在很多情况下，这种反比例关系能应用到傅里叶分析的复杂情况。
数学的引入
由于数学上有$sin$，$cos$，可以通过这些简单的表达式来表示周期性现象。
$cos(T+2\pi) = cos(T)$
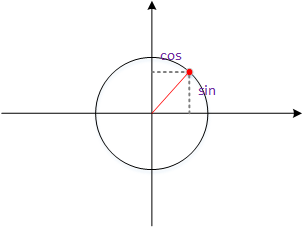
为什么$sin$、$cos$能表达空间上的周期性呢？因为$sin$与$cos$分别为单位圆的纵、横坐标，而圆在空间上市重复的对称的，走过一圈后会回到原点。
