[专题总结]线性代数和行列式相关

高斯消元

别忘记一个重要的性质就是在每个点关联的变量的方程并不多的时候，可以考虑带状矩阵消元，

还有一个就是带状矩阵不适用的时候，我们可以设置一些变量，然后把每个点用一个长度有限的关于这些变量的向量表示出来，最后用方程解出这些变量从而得到所有的值，有的时候巧妙的设计住主元是很重要的。

线性基

定义

• 线性组合

一些向量通过线性运算结合起来。

• 线性相关，无关

一组向量线性无关 \(\Leftrightarrow\) 这组向量中每个向量都不能被其他向量表示

• 张成空间

这组向量所有的线性组合。

• 基

一组向量张成空间的一个线性无关子集。

构建方式

把每个数依次插入线性基，若这个数已经能被线性基表示，则插入失败，否则插入成功。

具体实现，我们可以把线性基消成上三角基或者对角基来加速判断这个数能否被线性基表示的过程。

对角基有更多的性质，还可以直接用来求第 \(k\) 小。

对角基具体构建方式见 link

需要注意的一个小细节就是如果已经确定它可以插入线性基，消对角基的过程要先把他对低位的影响消掉再消除高位对他的影响，否则高位就会对低位产生影响了。

放一个代码

• code

struct Linear_Base{
    ull b[70], len = 30;
	
    bool ins(ull x){
	for(R i = len; ~i; i--) if((x >> i) & 1) if(b[i]) x ^= b[i]; else{
	    for(R j = 0; j < i; j++) if((x >> j) & 1) x ^= b[j];
	    for(R j = i + 1; j <= len; j++) if((b[j] >> i) & 1) b[j] ^= x;
	    return b[i] = x, 1;
	} return assert(!x), 0;
    }
} lib;

性质

• 线性基和原序列能异或出来的集合时相同的

1. 原序列的数都能被线性基表示，这是线性基的定义
2. 线性基只能表示原序列能表示的数，考虑线性基构建的过程，线性基内每个数都是由原序列异或得到的，所以线性基不可能异或出来原序列异或不出来的数。

• 线性基不能异或出来0，

若能，则说明线性基中肯定存在 \(x \oplus y=0\) 的集合 \(x,y\) ，那么 \(y\) 能被 \(x\) 表示出来，和线性无关相悖。

• 一个序列线性基内元素个数时固定的。

应用

最大权线性基

泛化模型：每个元素都有一个权值，要求求出原序列所有线性基里面权值最大的线性基。

如果原序列能够打乱，那么直接按权值从大到小排序，依次加入线性基就可以了，这也是 BJWC 元素 的做法。

不能打乱，考虑加入一个元素。
如果他的地方有值了，比权值，权值大的待在最高的地方，别忘了交换之后继续向后遍历，否则插入。
代码比较好理解， tim就是权值的时候可以用来带删线性基。

struct Linear_Base{
	ull b[70]; int tim[70], len = 40;
	
	bool ins(ull x, int ix){
		int tt = del[ix];
		for(R i = len; ~i; i--) if((x >> i) & 1){
			if(b[i] && tim[i] >= tt) x ^= b[i];
			else if(b[i] && tim[i] < tt) swap(tim[i], tt), swap(x, b[i]), x ^= b[i];
			else if(!b[i]) return tim[i] = tt, b[i] = x, 1;
		} return 0;
	} inline ull ask(int now){	int res = 0; for(R i = len; ~i; i--) if(tim[i] > now) if((res ^ b[i]) > res) res ^= b[i]; return res; }
} lib;

时刻维护权值最大的物品，配合扫描线贪心降维，把时间看作轴去思考，都是重要的启发

线性基合并

可以与和或，或比较简单，就是直接把一个包里插入另外一个线性基里面。

与的话，有一个朴素的想法是把一个线性基里面的数一个一个往另外里面插，插不进去就是交集。

这样又一个很明显的错误，就是线性基内的元素是可以调整的。

如果插进去了，他肯定不能作为答案，为了调整之后的元素，他就应该插在这个线性基里面。

如果插不进去，分两种情况：只被另一个集合的元素表示和被两个集合共同表示，被共同表示的时候，把他异或上自己集合的所有元素作为调整在加入答案即可。

利用异或的性质与其他结合

利用异或 “两次等于没有的性质”， 可以解决一些特殊的问题，主要集中于图论。

比如我们要找从 \(x\) 开始的异或最短路，我们可以进行以下操作给答案异或上 \(x\), \(x\) 是一个环的权值， 走到 \(x\) 所在环的一个点，绕 \(x\) 一圈，再走回去，其中到起点的路径经过两次被抵消了，我们可以直接给答案异或上 \(x\), 可以以同样的方法把两个环合并成一个环，所以把所有非树边形成的环插入线性基即可，之后我们只需要考虑 \(x,y\) 之间的简单路径。

还有比较典型的 DZY loves CHinese2, 求异或和为 0 的集合用来判断是否一些元素同时出现.

行列式

定义

\[det(A)=\sum_{k_1,k_2...k_n}(-1)^{inv(k)}*\prod_{j=1}^na_{j,k_j} \]

性质

零：关于逆序对函数

交换排列的相邻两项，逆序对的值改变1。

交换不相邻的两项，需要交换相邻的两项奇数次，所有交换排列的两个值会改变逆序对奇偶性。

附：上海森堡矩阵行列式，可以枚举当前这一行选择是谁，然后剩下的只能选对角线下面那一行，直到当前行选择列所在行，可以设计 \(dp\) 去递推，复杂度 \(O(n^2)\)。

一:几种特殊矩阵的行列式值

偷得图

证明考虑只有一种选择方案会使行列式的值不为0（从下到上归纳）。

二：转置之后行列式的值不变

要不叫行列式呢？行列当然是等价的。

证明考虑两个排列的所有组合情况就是相对运动，固定一个枚举另一个没有区别。

三：行列式两行交换，值变号

还是考虑定义式子，固定值不变，我们枚举到的排列就需要交换两项，奇偶性改变，故变号。

三+：行列式两行相等，行列式值为 \(0\)

比较巧妙的证明：既然交换两行要变号，那么交换两行相等的也要变号， \(x=-x \Rightarrow x=0\)

根据定义证明：只考虑这两行在排列里面的选值，总情况是 \(n*(n-1)\) 的，每一种 \(i,j\) 都映射一个 \(j,i\)，其中他们的值相同，符号相反。

四：行列式一行上的 \(\gcd\) 可以提出来

考虑定义式子，选到哪个都要乘上 \(\gcd\) ，所以可以提出来。

三+四：行列式上有两行成比例，值为 \(0\)

五：行列式的“裂项”

\[\begin{vmatrix} a & b & c\\ d + u& e +i& f+o\\ g & h & k \end{vmatrix} \Rightarrow \begin{vmatrix} a & b & c\\ d & e & f\\ g & h &k \end{vmatrix}+\begin{vmatrix} a & b & c\\ u & i & o\\ g & h &k \end{vmatrix} \]

类似线性性吧，拆一下定义式发现显然正确。

这条性质用来构造我们需要的行列式，比较好用

六：把一行成比例加到另一行上，行列式值不变。

考虑裂项，再提出来那一行的 \(\gcd\)，后面的行列式值为0。

定理

余子式，代数余子式，按行展开

余子式就是去掉 \((i,j)\) 所在的行和列之后剩下的矩阵的行列式，记做 \(M_{ij}\)

代数余子式 \(A_{ij}=(-1)^{i+j}M_{ij}\)

行列式按一行展开计算（此处按第 \(i\) 行展开）（同理可以按列展开）

\[det(A)=\sum_{j=1}^na_{ij}A_{ij} \]

证明考虑枚举当前行选择的是谁，假设选的是 \(j\) , 那么我们计算上他对逆序对和值的贡献去递归即可，由于当前这一行选任意元素我们都枚举到了，所以计算是正确的。

对值的贡献显然是 \(a_{i,j}\) , 考虑对逆序对的贡献，枚举 \(i\) 前面有 \(k\) 个大于 \(j\) 的，那么前面有 \(i-1-k\) 个小于 \(j\) 的，后面有 \(j-1-(i-1-k)=j-i+k\) 个小于他的，对逆序对贡献 \((-1)^{k+j-i+k}=(-1)^{j-i}=(-1)^{j+i}\) 。

异乘变零定理

\[\sum_{i=1}^na_{ji}*A_{ki}=0 \ \ \ (j\not= k)\]

证明考虑矩阵按第 \(k\) 行展开，那么我们把第 \(k\) 行替换成第 \(j\) 行， \(a_{ji}*A_{ki}\) 是不变的。

但是被替换的矩阵中有两行相等，所以行列式值是 \(0\)。

拉普拉斯展开

按一行展开的扩展版，和按一行展开一样证明，提前计算逆序对的贡献，不写了手累

\[det(A)=\sum_{1\leq j_1< j_2<...<j_n\leq n}A\begin{pmatrix} i_1 & ... &i_k \\ j_1 & ... & j_k \end{pmatrix}(-1)^{(\sum_k i_k+j_k)}\begin{pmatrix} i^{'}_1 & ... &i^{'}_{n-k} \\ j^{'}_1 & ... & j^{'}_{n-k} \end{pmatrix} \]

后面是前面的子式的余子式，前面的就是选出来 \(i_1..i_k,j_1..j_k\) 这些行和列相交的地方组成的行列式。

后面的就是去掉这 \(k\) 行列剩下的矩阵的行列式，选定 \(i\) 行之后枚举 \(\binom n k\) 列就可以计算行列式。

伴随矩阵定理

定义代数余子式矩阵 \(cof_{ij}=A_{ij}\) 也就是 \((i,j)\) 的代数余子式放到这个矩阵的 \(i,j\) 位置。

定义伴随矩阵为 \(^*A=cof^T\) 也就是他的转置。

有公式

\[A\times^*A=^*A\times A=det(A)*I \]

等式最右边就是单位矩阵只有行等于列的地方有值，值为原矩阵行列式的值。

证明的话直接把 \(^*A\) 的定义带进去展开，可以发现只有行等于列的时候是按一行展开的计算式，其他情况都是异乘变零定理。

柯西-比内公式

设 \(A\) 是一个 \(n*m\) 的矩阵， \(B\) 是一个 \(m*n\) 的矩阵，那么 \(det(A*B)\) 可以根据此公式计算

\[det(A*B)=\begin{cases} 0 & \text{ if } n > m \\ det(A)*det(B) & \text{ if } n=m \\ \displaystyle \sum_{1\leq j_1<j_2<...<j_n\leq m} det(A {\begin{pmatrix} 1 & ... & n\\ j_1 & ... &j_n \end{pmatrix}}) *det(B\begin{pmatrix} j_1 &... & j_n\\ 1 & ... & n \end{pmatrix}) & \text{ if } n < m \end{cases} \]

其中这个括号代表选出这些行和列构成的子式。

证明有一个非常巧妙的分块矩阵法。

构造 \(N=\begin{vmatrix} \mathbf{A} & \mathbf{0}\\ \mathbf{-I} & \mathbf{B} \end{vmatrix},M=\begin{vmatrix} \mathbf{0} & \mathbf{AB}\\ \mathbf{-I} & \mathbf{B} \end{vmatrix}\)

可以证明 \(det(N)=det(M)\)，方法是枚举第 \(1 \leq k \leq n\) 行，再枚举第 \(1 \leq j\leq m\) 列。

把 \(N\) 矩阵中的 块 \(A\)矩阵里面的 \(A_{k,j}\) 乘到第 \(j+n\) 行上再加到第 \(k\) 行上。

（其实就是尝试把 \(A\) 消成0的过程，然后发现那个 \(0\) 根据矩阵乘法定义自然变成了 \(AB\)）

然后可以发现 \(det(A*B)=(-1)^m*det(M)\) 。

因为对于上面的 \(n\) 行，你必须在 \([m+1,m+n]\) 内选择保证行列式值不为0，对于下面的 \(m\) 行，已经只能在 \([1,m]\) 内选择，为了值不为0，必须选择 \(-I\) 的对角线,这样算出来就是 \(AB\) 的行列式多了个 \(N\)。

现在开始分情况证明。

• 若 \(n>m\) ,在 \(N\) 矩阵中怎么选都会选到 \(0\) （上面 \(n\) 行要选择 \(n\) 个数，然而只有 \(m\) 列有非0的数）、

所以 \(det(A*B)=(-1)^m*det(M)=(-1)^m*det(N)=0\)

• 若 \(n=m\) ,在 \(N\) 矩阵中只有一类选法使得答案不是 \(0\), 那就是在上面 \(n\) 行选择 \(A\) 矩阵，下面 \(n\) 行选择 \(B\) 矩阵。

所以按照定义写开可以得到 \(det(A*B)=det(A)*det(B)\)

• 若 \(n<m\) ,在 \(N\) 矩阵的前 \(n\) 行选择 \(A\) 矩阵的若干列，那么这些选择的这些列必定也得在下面 \(m\) 行选择那些行。
  放个图片比较好理解，反正就是 \(A\) 选择的列和 \(B\)选择的行必须对应

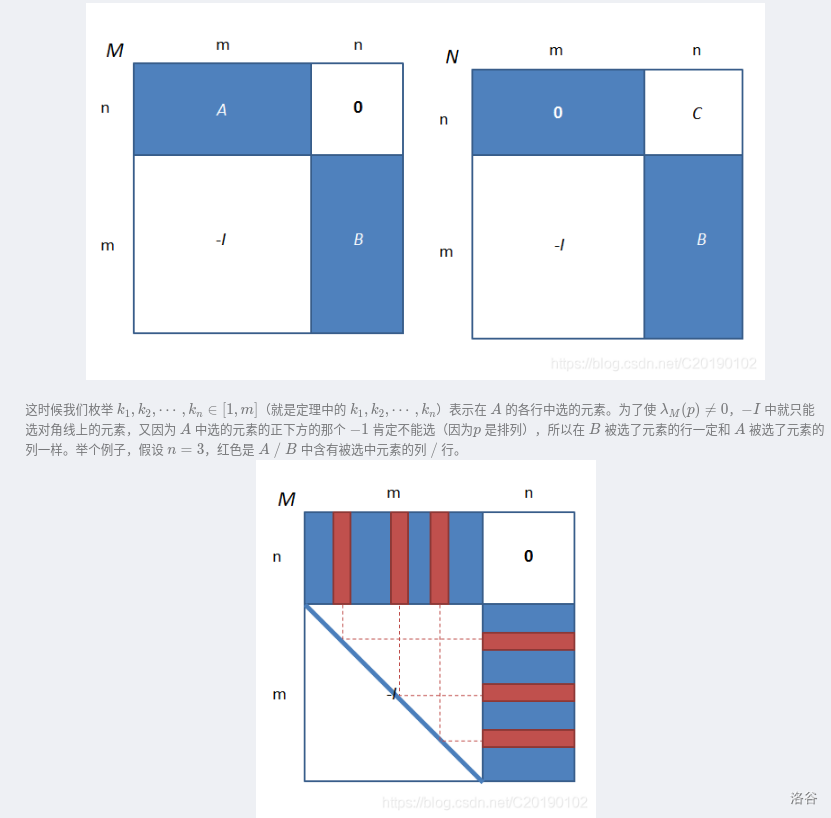
所以得证了。

线性代数习题

NOI模拟 6.23 B

先考虑把原矩阵每一行减去它上面那一行，考虑这么做会使矩阵变成什么样子。

第 \(i\) 行， 第 \(i-1\) 列是 \(C-1\) ，第 \(i\) 列是 \(1-C\) , \(i\) 的倍数处是 \(-C\), \(i-1\) 的倍数处是 \(C\) （同时是是 \(C-C=0\)）

不难发现，假设前面的都处理好了，我如果在第 \(i\) 行不选择第 \(i\) 列，那么第 \(i\) 列上就只能由 \(i+1\) 来选择。

这种状态将持续，直到你在第 \(i\) 行选择的第 \(k\) 列所在的行。

考虑设计一个 \(Dp, Dp_{i}\) 代表前 \(i*i\) 的矩阵的行列式，转移，当前在第 \(i\)， 考虑第 \(i+1\) 列选什么。

转移的时候发现这堆 \(C-1,1-C\) 严重影响我们，不妨把所有元素除掉 \(1-C\), 令 \(v= \frac{C}{1-C}\)

选择 \(i+1\) 行 ： \(f_{i+1} \leftarrow f_{i}\)

选择上面的一个 \(C\) : \(f_{i+1} \leftarrow v*\sum_{j|i}-f_{j-1}\)

选择上面的一个 \(-C\) : \(f_{i+1} \leftarrow v*\sum_{j|i}f_{j}\)

有两点值得注意 : 第一点是把 \(0\) 拆成 \(C, -C\) ，这步只需要我们思考这个矩阵的实际意义即可。

第二点是逆序对的贡献，发现我们选择 \(i\) 个对角线下面的 \(-1\), 逆序对会贡献 \((-1)^i\), 所以 \((-1)^{i+i}=1\) ，逆序对不造成贡献。

这种特殊的矩阵的行列式，直接思考怎么求也是一种办法，我考场一直在想怎么搞成更简单的行列式了。

观察这个转移柿子 \(f_i=f_{i-1}+v*\sum_{j|i} f_j-f_{j-1}\) , 不放令 \(g_i=f_i-f_{i-1}\) 。

那么转移可以写成 \(g_i=v*\sum_{j|i} g_j\) ，可以发现他是 \(g=g*\frac{v}{v+1}\) ， 根据杜教筛的定义化柿子即可。

当数据范围比较像前缀和筛法的时候，不妨尝试把你要的东西差分。

发现这题卡我们预处理的时候带 \(log\)， 观察 \(g\) 的转移，质因子指数可重集一样，答案就一样。

故现行筛每个数的可重集hash，然后只在最小的地方计算转移，最后再前缀和起来即可，复杂度 \(O(n^{\frac{2}{3}})\)。

本题还有一个做法，首先需要发现一个东西：如果取出几行几列矩阵全都是 \(C/0\) 。

那么有一个关键性质：这几行构成的乘除意义下的偏序集必须是一条链，行列式才有值。

归纳证明即可，然后我们考虑怎么把行列式变成那个样子，现在的问题是主对角线上有 \(1\) 。

我们把主对角线全部变成 \(C\) ，然后枚举主对角线上选择元素的集合，乘上 \((\frac{1}{C})^{sz}\) 即可。

计算集合恰好是他可以考虑容斥，要求是剩下的不能选对角线，再枚举一个强制选的集合，然后剩下的随便选，可以套用上述结论。

最后套路的对每个随便选统计容斥系数之和即可，只有乘除链处有值，计算可以写成递推式。

省选模拟4.6 B

这种奇减偶加的先往行列式上面凑，发现行列式摆在脸上，我们把矩阵第 \(i\) 行 \(L_i-R_i\) 设成 \(1\) ，答案就是行列式。

现在问题是怎么快速消这个看起来很特殊的矩阵，我们先把区间按左端点排序，考虑把他整成上三角。

对于每个相同的左端点，我们把它用最小的右端点消所有其他的右端点，那么其他的区间就没有左端点是他的了(把被削的区间更新到新的左端点上)，就可以在这一列上选择他。

就这么递归下去，可以发现我们可以消成上三角，否则无解，可并堆可以维护上述操作。

Prufer序列

这个东西主要就是用来对树计数，一般知道 Cayley 公式计数就够用了，Prufer序列用处很局限。

首先，Cayley 公式指出无向完全图有 \(n^{n-2}\) 个生成树。

这个东西证明就用 prufer 序列， 他的证明方法是大名鼎鼎的 “构造即证明”。

把一个树每次删掉度数最小的叶子节点，直到剩两个点，就会构造出来一个n-2的序列。

树映射序列是单射很显然，序列映射树是单射也可以证明，同样是构造。

记一下 \(O(n)\) 的代码吧，思路是开一个指针维护当前标号最小的叶子。

code

struct Prufer{
	int now, ptr, dr[N], leaf[N], ans[N];
	vector<int> v[N];

	void dfs(int x, int fa){
		if(fa) ans[x] = fa;
		for(auto y: v[x]) if(y != fa) dfs(y, x);
	}

	void prufer_to_tree(int *prufer){
		for(R i = 1; i <= n; i++) dr[i]++;
		for(R i = 1; i <= n - 2; i++) dr[prufer[i]]++;
		for(R i = 1; i <= n; i++) if(dr[i] == 1){ now = ptr = i; break; }
		assert(now && ptr);
		for(R i = 1; i <= n - 2; i++){
			int f = prufer[i]; ans[now] = f;
			if(--dr[f] == 1 && f < ptr) now = f;
			else{ ptr++; while(dr[ptr] != 1) ptr++; now = ptr; }
		} ans[now] = n;
		//dfs(n, 0);
	}

	void tree_to_prufer(int *fa){
		for(R i = 1; i < n; i++) dr[i]++, dr[fa[i]]++;
		for(R i = 1; i <= n; i++) if(dr[i] == 1){ now = ptr = i; break; }
		for(R i = 1; i <= n - 2; i++){
			int f = fa[now]; ans[i] = f;
			if(--dr[f] == 1 && f < ptr) now = f;
			else{ ptr++; while(dr[ptr] != 1) ptr++; now = ptr; }
		}
	}
} pr;

Purfer 题目

树的计数

给出每个点度数问对应的树有多少种。

prufer序列的性质就是度数为 \(i\) 的点会在序列内出现 \(i-1\) 次，所以答案就是个多重集排列。

明明的烦恼

给出一些点的度数问对应的树有多少种。

同理，先把给出的多重集排列，没给出的就是随便选 (LLA)

城市地铁规划

先把给定的多项式对 \(0\sim n-1\) 都计算了，记为 \(g_i\) 。

现在就是每个点可以选择一个度数，选择一个度数会有对应收益，问最后的最大收益。

暴力去背包，复杂度是 \(n^3\) 的，这是因为每个点都有很多物品，你要枚举去选哪个。

但是发现虽然每个点有很多物品，但是他们都是相同的，我们只需要统计每个物品被选几次就好了。

这样去背包，复杂度是 \(n^2\) 的，记录一下前驱，弄完之后用 prufer 序列构造出来树就好了。

Clarke and tree

给定每个点的度数上限，问大小为 \(1-n\) 的树分别有多少种。

本来想容斥，但是 \(n \leq 50\) 好像需要多项式算法，所以去考虑 \(dp\) 。

大体思路就是去构造 prufer 序列， \(f_{i,j,k}\) 代表前 \(i\) 个数，选择了 \(j\) 个点， prufer序列构造到第 \(k\) 位的方案数。

转移的时候首先考虑这个点选不选，再考虑往prufer序列里面放了几个，转移的时候顺便维护一下多重集排列就行了。

铬合金之声

很妙的思维题，感觉自己做出来会比较有成就感。

首先可以看出来一定是 \(n-m\) 个树组成的森林。

每个森林的贡献是他的大小，可以视作在里面选择一个点，也可以看做选出来一个点作为根。

选出来 \(n-m\) 个根的方案数就是 siz 之积，所以就是需要求 无向图有根数森林计数。

森林计数显然不会，造一个虚拟点向每一个根去连边，就是树计数了（删掉这个点将变成森林）。

之后就是强制这个点的度数球方案数了，做法同 【明明的烦恼】。

一共两步转化，都非常秒，是不可多得的好题。

The Cities And Roads DivTwo

给定 n 个点的 k 个联通块，问加 k-1 条边使得全图联通的方案数。

也是 扩展 Cayley 公式，答案是 \(n^{k-2}*\prod siz_i\) , siz 是联通块大小。

简易但也正确的证明：先当做 \(k\) 个点，他的 prufer 序列长为 k-2 , 每个地方都可以放 n 个数中的一个。

至于后面那一坨，每个点被删掉的时候会统计他的父亲一次，他的父亲的方式确定了，但是他还有 \(siz_i\) 种选法。

最后剩下两个联通块，之间的连边有 siz 相乘种选法，所以可以得到那个公式。

当然还有枚举 度数序列 之后多元二项式定理的，也比较简洁巧妙 OI-wiki

还有一个通过矩阵树定理+手消行列式的证明操作，尽请期待下文

The Cities And Roads DivOne

给定 n 个点的 k 个联通块，问条边使得全图任意两个点之间都有 (1-2) 条简单路径的方案数。

首先不难发现最终答案不是树就是基环树。

树的情况直接和 Div Two 一样，考虑基环树，我们分情况讨论。

他给出的图里面就有环，好了直接当树做。

剩下的我们去状压枚举把哪些联通块搞成一个环（直接在统计出来的树上加边会重复）

若只选中了一个联通块，答案是 \(\binom{siz}{2} -m\) , 选中了两个，答案是 \(\binom{siz_a*siz_b}{2}\)

选中了大于等于三个， 答案是先圆排列一下再统计选法， 注意一个圆的两种顺序只能算一次 ，答案是 \(\frac{(k-1)!}{2} \prod siz^2\)

CF917D

联通块=点数-边数，这个是经典套路。

我们先来一个爆 CF 标算的 \(n^3\) 算法， 考虑 Ex Cayley 公式。

发现有了这个公式之后，我们只需要知道联通块个数 和 联通块大小之积的和就行了，后一个看起来就很可 DP 的样子。

\(dp_{x,i,j}\) 代表 x 子树内保留 i 条边，和 x 联通的联通块大小是 j 的联通块大小之积的和。

转移也很简单，就去子树合并。

转移就去子树合并, 假设现在有 \(f_{x,i,j},f_{y,k,l}\)

合并，相乘转移到 \(f_{x,i+k+1,j+l}\) , 转移系数是 \(\frac{j+l}{j*l}\)

不合并，相乘转移到 \(f_{x,i+k,j}\) , 转移系数是 1。

然后考虑怎么去 \(n^2\) ，重新审视需要求的东西 \(\sum\prod Siz_i\)

也就是划分出 \(n-1\) 个联通块，在每个联通块内选择一个点的方案数（和上面那个一样

都是式子到组合意义，类似还有 ARC124E， 那么重新设置 DP 状态

组合意义是优化 Dp 的方法，尤其见到 \(\prod\) 组合数之类的东西。

\(dp_{i,j,0/1}\) 代表 \(i\) 子树内保留 \(j\) 条边，选没选点的方案数。

转移也很简单，一共四条，分别考虑合不合并和0/1。

\(dp_{x,i,0}*dp_{y,j,1} \rightarrow dp_{x,i+j,0}\)

不合并，不合并之后的联通块没有选择点，那么原联通块必须没有选择点。

但是y的联通块从此就封闭了，所以他必须选择一个点。

\(dp_{x,i,1}*dp_{y,j,1} \rightarrow dp_{x,i+j,1}\)

不合并，和上面同理。

\(dp_{x,i,1}*dp_{y,j,0}+dp_{x,i,0}*dp_{y,j,1} \rightarrow dp_{x,i+j+1,1}\)

合并之后选，那么之前两个必须有一个选择的。

\(dp_{x,i,0}*dp_{y,j,0} \rightarrow dp_{x,i+j+1,0}\)

合并之后不选，那么之前两个必须都不选。

P5206 [WC2019] 数树

和上面一个题的做法一样，第二维 \(+1\) 变成 \(*y\) 即可。

矩阵树定理

用来计算一张图生成树个数，就是把一张图的（度数矩阵-邻接矩阵）去掉任意一个 \(i\) 的第 \(i\) 行，列求行列式。

有向图可以计算根向树和叶向树的个数， 根向树 （出度矩阵-邻接矩阵）， 叶向树 （入度矩阵-邻接矩阵）。

证明比较厉害，我们证明无向图的形式，有向图与其类似。

我们任意钦定一个点作为根，然后让其他点任意选择一条边去连上，那么图肯定变成了若干个基环树或者恰好一个树。

考虑对环去容斥，那么我们枚举环的数量，强制他们选择，那么就要有 \((-1)^i\) 的容斥系数。

排列可以表示成若干个置换环，里面有 \(i\) 个置换环，就让答案乘 \((-1) ^i\) ，特别的， \(i\) 选 \(i\) 并不是自环，而是让他任意选择，所以在每个 \((i,i)\) 乘上 \((-1)\) 来抵消它带来的影响。

那么现在我们的答案就是 $\sum_{p} (-1)^{\tau (p)} \prod w_{i,p_i} $ 。

现在的问题就是找到置换环的奇偶性和逆序对的奇偶性之间的关系。

考虑把一个排列 \(p\) 调整成 \(1,2,..,n\) ，需要交换的次数是 \(p\) 的逆序对。

因为他被拆成了 \(k\) 个置换环，每个置换环内可以通过 \(len-1\) 次交换来排序 (把最小的换到第一个，然后变成一个 \(len-1\) 的置换环，即可归纳)， 所以总共需要 \(n-k\) 次交换能让排列有序，也就是 (n-置换环数)=(逆序对数) [在奇偶性的意义下]。

然而我们计算的系数是 \(k\) ，所以让每个地方的系数都乘 \(-1\)，就得到了矩阵树的形式。

省选模拟 4.1 B

CF578F Mirror Box

P4033 [Code+#2]白金元首与独舞

CF53E Dead Ends

ABC253 Ex - We Love Forest

手消行列式

对于一些特殊的图，我们可以得到基尔霍夫矩阵之后手动消元来得到更优秀的表达式。

Cayley 公式证明

Ex Cayley 公式证明

完全二分图生成树

小练习-1

• n 个点，每个点有颜色，同色点不能连边

小练习-2

• 有 \(P\) 个连通块，第 \(i\) 个连通块颜色为 \(c_i\)​，点数为 \(t_i\)​。同色连通块不能相邻。问再把这些连通块连成一棵树的方案数，（\(\sum t_i=n\)，颜色数为 \(k\)。）

奉行大力手玩，乱凑的原则，不要局限于消得剩下一个三角，只要保证它剩下一种选法即可。

Best 定理

用来求一个 有向图 的欧拉回路的数量, 公式是 \(\prod (deg_i-1)!A_x\) , \(A_x\) 是以任意一个点为根的内向生成树的个数。

证明考虑先找到一个内向生成树，然后给每个点的非树边钦定一个顺序，走到这个点的时候按顺序走这些出边，最后走树边。

这样肯定经过每条边最多一次，但是问题是有可能走一半走不一下去了吗？ 假设走到 \(x\) 走不下去了，那么由于入边和出边相等，容易知道这是矛盾的，所以肯定可以遍历每条边恰好一次。

怎么证明所有的欧拉回路都被统计了呢？ 考虑一条欧拉回路肯定有经过每个点出度的顺序，只需要证明每个点走后的出边不会成环即可，假设他走的最后一条边成环了，那么他还要再走出去一次，和成环矛盾，所以不可能（根结点不可能在环上，因为没有出边。

要求以某个点为起点/终点的欧拉回路个数，那么直接乘上这个点的 deg 即可，他在欧拉回路的每次出现都可以挪到开头作为一个合法的贡献。

Lgv 引理

给定 \(n\) 个起点 \(A_i\) 和终点 \(B_i\)，是一个 DAG, 定义一组无交路径为 \(n\) 条 \(A_i \rightarrow B_{p_i}\) 的路径，满足点不相交，他们的权值是这组路径上所有边的乘积。

\(Lgv\) 用来求逆序对是偶数的权值和-逆序对是奇数的权值和，他就是把 \(A_i \rightarrow B_j\) 的路径方案数填到矩阵的 \((i,j)\) 处，矩阵的行列式。

证明考虑这个东西其实是不满足不相交的，但是我们发现一组存在相交的路径肯定可以把这两个路径的后半段交换一下，权值不变，逆序对改变，然后就抵消了。

一般来说，很多图都满足路径不相交，那么只能是 \(1,2,3..,n\) 这一个排列有贡献，于是可以用来路径计数

网格图就是一个很好的例子。

CF348D Turtles

不相交立马就 lgv， 把 \((1,1)\) 变成 \((1,2)\) 和 \((2,1)\), \((n,m)\) 变成 \((n-1,m)\) 和 \((n,m-1)\) 。

由于是网格图，路径不想交，那么直接组合数算算在高斯消元即可。

Monotonic Matrix

我们发现 \((0,1),(1,2)\) 之间的分界线是 \((1,m) \rightarrow (n,1)\) 的两条路径，其中第二条不能跨越第一条。

我们 lgv 求的是不相交的，你要不跨越的，那么我就把一条向下平移一格，平移之后的一条不相交路径对应一条之前的不重合路径。

平移把不跨越变成不相交是经典操作， Catlan 也用到了。

ABC216 H

还是路径不相交，但是这次我们不知道终点。

考虑 \(lgv\) 的本质，其实是枚举逆序对去容斥，我们列出一格枚举终点的柿子。

\[\sum_{\{y_1,y_2...,y_k\}} (-1)^{\tau(y)} \prod \binom{n}{x_i-y_i} \]

这个容斥柿子，我们使用经典的 \(Dp\) 计算容斥的套路，从小到大枚举 \(y\) ，枚举当前加入谁，逆序对容易计算。