题解大合集
upd 2021.12.7:这篇blog也许永远也不会完结了,因为联赛后的任务肯定比联赛前更重。
一些考试题,有的场改的不多,或者懒得去找那一场了,捡几道想写的写写题解。
同时感觉一些题不错,也会重新看一遍重新写题解(或者抄过来)。
本篇大概是我认为除了dp题之外不错的题(也就是这篇无dp)。
模拟57-2D,模拟53-午餐,虽然很nb,但我丝毫没思路,感觉是毒瘤图论题,先不写了。
冲刺17-寻找道路
我感觉挺 \(NB\) 的题,但是大佬们都考场切了。
一个切入点就是最终答案不取模数会很大,所以要想比大小不太现实,也就是最短路应该舍弃,所以考虑类似 \(bfs\) 的东西。
首先可以把和1连边为0的点缩成一个团,那么到每个点,距离最短是优先的。
同时要保证字典序最小,考虑 \(zfs\) ( ZZ_zuozhe 优化的 bfs ,简称zfs(ZZ_zuozhe first search))。
zfs可以用来处理字典序问题,思路就是时刻保证队列里面 ZZ优先 按字典序排序。
由于字典序扩展具有单调性,\(zfs\) 的 \(bfs\) 性质保证了二段性,所以可以这么做,但是需要保证字典序单调扩展。
保证的方法就是每次取出队列中字典序相同的所有元素,先扩展0在扩展1。
可以扩展到更高的进制,复杂度为 \(O(kn)\) , k是进制数。
应该观察性质,无法进行比较舍弃最短路是解决这题的关键。
口胡比赛1T1
把操作转化成差分
冲刺16-铺设道路
模拟10-星空
ACwing100
Acwing239
模拟62-Set
建出来序列的前缀和,在模 N 的意义下有 N+1 个值,那么对前缀和差分一下,得到的就是一个区间的和。
这题的突破点其实在 N 个数整除 N ,题目中有一些没什么关系的变量莫名相等,有可能就是突破点。(同,可以crtl+F ACwing146)
差分之后找到的两个相等的前缀和,对应的区间就是可以被 N 整除的,必定可以找到相等的,因为一共N+1个数,N个值。
毕竟在取模意义下做差可以的到有意义的东西,那么就构造出来可以做差的东西,也就是前缀和了。
复杂的区间信息
模拟81-斐波
好题,线段树维护矩阵,\(zero4338\) 真 \(NB\) 。
首先需要发现维护三个量就可以线性递推 \(fib^2\) 。
也就是 \(fib^2_i,fib^2_{i+1},fib_i*fib_{i+1}\) ,转移很显然,可以写成矩阵,记这个矩阵是 \(tran\) 。
考虑直接维护 \(f(S)=\large\sum\limits_{T\subset S}fib^2(sum(T))\) ,因为都是加和起来的,所以还可以像上文一样转移。
考虑给 \(S\) 加入一个元素 \(x\) ,那么新的所有子集就是 原来的所有子集和原来的所有子集 \(\cup x\) 。
考虑新加入一个 \(x\) , 那么就是给每一个 \(sum\) 都加上x,也就是转移 \(tran^x\) 。
所以在每个点,假设原矩阵是 \(B\) , 转移相当于是 \(B*=(I+tran^{a_i})\) ,记 \(Z_i=(I+tran^{a_i})\) 。
那么问题变成了单点修改 \(Z_i\) , 区间查询 \(\sum\limits _l\sum\limits _r\prod\limits _{k=l}^rZ_k\) 。
考虑只有一个询问,那么分治去做,记 \(Ans=\sum\limits _l\sum\limits _r\prod\limits _{k=l}^rZ_k\) 。
拆一下,发现前两维本质是在枚举所有区间。
所有区间可以拆成 \([l,mid]\) 所有区间+\([mid+1,r]\) 所有区间+左端点在 \([l,mid]\),右端点在 \([mid+1,r]\) 的区间。
前两个分治去做,考虑计算最后一个,写出来就是 \(\sum\limits_{ll=l}^{mid}\sum\limits_{rr=mid+1}^{r}\prod\limits_{k=ll}^{rr}Z_k\)
把最后一个东西拆开,在提出来独立部分,化简成 \(\sum\limits_{ll=l}^{mid}\prod\limits_{k=ll}^{mid}Z_k\sum\limits_{rr=mid+1}^{r}\prod\limits_{k=mid+1}^{rr}Z_k\)
那么发现可以 \(O(n)\) 计算 \(suf_{[l,r]}=\sum\limits_{ll=l}^{r}\prod\limits_{k=ll}^{r}Z_k\) , \(pre_{[l,r]}=\sum\limits_{rr=l}^{r}\prod\limits_{k=l}^{rr}Z_k\)
所以一个询问就做完了,考虑多个询问,那就在线段树上每个节点存下来 \(pre,suf,ans,mul\) , 前三个作用和上文相同,最后一个就是这个区间内所有矩阵的乘积。
这个应该是套路,对于这种多次询问一个区间内复杂信息的时候,考虑一个询问如何在正确复杂度内回答,然后用线段树优化,一般需要存多个信息辅助转移。
然后合并区间推一推就行了,这个不难,同时维护多个信息去转移,类似 \(Omeed\) 。
模拟31-Game
当时的1个log就是用更nb的线段树能在线段树上二分,先记一下2个log做法。
首先如果我们可以 \(O(log)\) 的计算一个序列已知自己手牌情况下的最大得分,那么在每一个地方二分。
二分后删掉这张牌,就变成了一个子问题,那么 \(O(log)\) 计算用这张牌对答案有没有影响就行了。
在考虑怎么 \(O(log)\) 计算,权值线段树维护信息就是这个区间内的得分,每个点A的牌数,B的牌数。
合并信息的时候,这个区间内的得分其实就是 左区间得分+右区间得分+左右区间贡献的得分,也就是 \(min(A[l],B[r])\) 。
修改直接改 \(A,B\) 就行,其实是线段树优化分治的过程。
这个分治确实有点diao,即使第二遍做仍然没有想到,为什么yspm说是贪心?一直无法理解,yspm也不告诉我(欺负我菜。
线段树优化分治是常见套路,求区间信息先想能否分治,再看能否把信息存下来用线段树优化
模拟47-Omeed
同样是很麻烦的一个信息维护,基础分很简单,考虑计算连击分。
首先可以考虑 \(O(n)\) dp, \(f_i=p_i*(f_{i-1}+1)+(1-p_i)*t_i*f_{i-1},ans+=p_i*(f_{i-1}+1)\)
发现整个柿子移个项都是关于 \(i-1\) 一次函数的形式,这个东西可以用线段树维护。
具体还是推柿子,把这个区间内所有的数用 \(f_i=k*f_l+b\) 的形式去表示。
然后缺啥维护啥,要维护五个东西,这个区间的最右边的 \(k,b\) , 区间 \(k,b\) 的和,和这个区间的 \(p\) 的和。
然后大力推柿子就可了,注意把 \(p_i\) 也看成常量,线段树维护一次函数的套路也许就是这样,把所有的东西用左端点表示。
模拟56-底垫
简化题意:给定 \(n\) 个区间 \([l_i,r_i)\),再给定 \(m\) 次询问,每次给一个 \(a,b\) , 求 \(\sum\limits_{l=a}^{b}\sum\limits_{r=l}^{b}\bigcup\limits_{k=l}^{r}[l_k,r_k)\) , \(n,m\leq 1e5\) 。
同样是很复杂的区间信息维护,但是没有修改,所以可以考虑离线询问。
现在考虑只有 \(\bigcup\limits_{k=l}^{r}[l_k,r_k)\) , 如何回答 \(1e5\) 个询问。
像这种问题一般都可以考虑扫描线+数据结构维护,也就是扫描一个端点,在数据结构上维护另一个端点的答案。
在值域上开一个 \(set\) , 维护每个点最后出现在哪个梦境中。
把询问用右端点离线到梦境轴上面,然后扫描梦境轴,时刻维护当前点为右端点所有左端点的答案。
在 \(set\) 中加入当前右端点的梦境,它的梦境肯定覆盖了其他的梦境 (初始一个轴都是0的梦境),假设它覆盖了一条长度为 \(k\) , 出现时间在 \(t\) 的梦境 。
所有在 \([t+1,i]\) 内的左端点都可以增加 \(k\) 的贡献 , 并且由于维护的是最后出现的梦境,还要把自己这条梦境插入 \(set\) 。
再考虑回到本题,显然我们已经不太能让维护的东西更多了,那就直接考虑当前的东西对最终答案的贡献。
若一个区间 \([l,r],l\in [t+1,i]\) , 那么当前这个梦境对这个区间的贡献是 \((i-l+1)*(r-i+1)*k\)
因为这个 \(k\) 会被计算这么多种选法计算到。
若它的 \(l\in [1,t]\) , 那么它的这条线段的贡献在之前已经计算过了,但是这里并不能不叠加,因为区间选到这里也会有贡献。
那么就考虑这个新位置对他的贡献,不难写出 \((i-t)*(r-i+1)*k\)
本题和简化版的不同就是要时刻维护所有点的贡献,而不是只维护新增的贡献。
这也为求一个区间的所有子区间的信息提供了一个思路,考虑这个区间内每个点对最终答案的贡献。
上述式子拆开,在左端点维护 \(l,r,lr\), 常数 的贡献就行了。
这个维护系数其实是挺妙的,完美的在左端点独立了右端点,从而解决了本题。
当时看题解的时候感觉难度并不是很大,重新思考一点思路都没有,wtcl。
把边之间连边
模拟80-滑稽树下你和我
考试的时候并没有想到在边上迂回这种神器操作,于是爆炸了(幸亏我感觉这题不可能这么简单然后没写)。
所以事情从简单做起,先考虑没有边上的简单情况。
二分答案 \(mid\) ,之后开始 \(bfs\) ,定义状态 \(f_{x,y}\) 为 \(A\) 在x, \(B\) 在y是否合法。
一个状态合法的条件就是同时满足一下两条:
- 他由一个合法的状态走过来
- 满足 \(dis(x,y)\leq mid\)
每次刷表,有以下转移 , ( \(to_x\) 代表 \(x\) 能到达的点 )
- \(A,B \rightarrow to_A,B\)
- \(A,B \rightarrow A,to_B\)
- \(A,B \rightarrow to_A,to_B\)
最后直接看能否存在一个状态 \(A,B\) , 使得他们度数都是就好了。
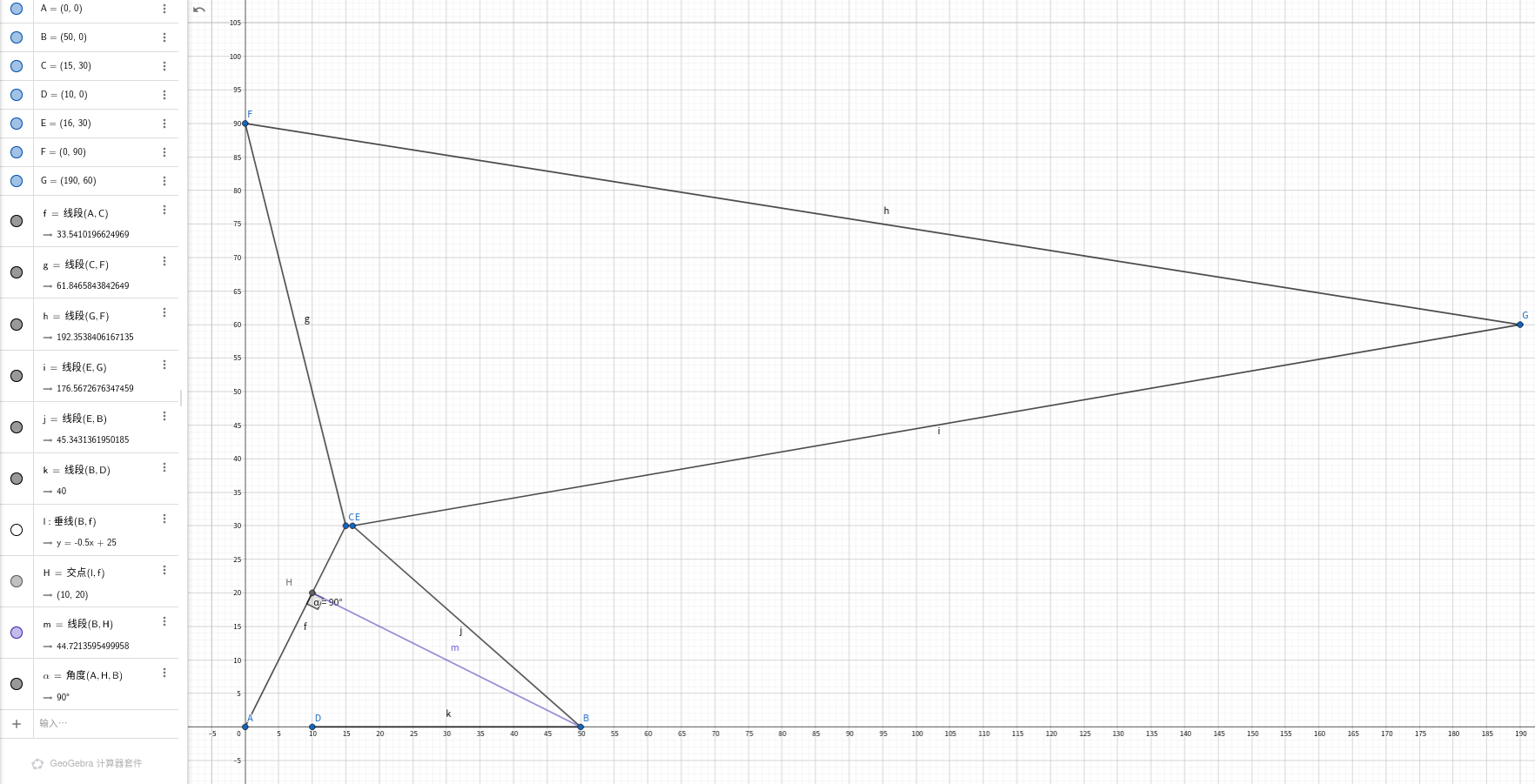
但是这个为什么不对呢?考虑以下情况( 提供样例,答案是44.721360)
7 1 5
0 0
50 0
15 30
10 0
16 30
0 90
190 60
2 4
1 3
2 5
3 6
6 7
5 7
这样构造图的原因是只让(A,E)走到(A,D)
如果朴素的走,那么我们只能让(A,E)->(A,B)->(A,D)。代价为50;
一开始,A,E有点,我们可以先让A走到H,然后让E走到B,代价为44.721360
先让B走到D,再让H回到A ,没有额外代价。
为了处理这样的情况,把边也建成一个点,让边和其两边的点连边,边和点的距离用数学知识算一算就好啦!
题解里面说有边和边的距离,我发现并没有这种情况,所以没写,也是对的,如果有人发现有这种情况,欢迎直接打脸。
把它搬运过来,原因是要提醒自己好好分析题意,还有注意把边建成点的套路。
模拟61-交通
和上文一样是边看成点连边,但是和上文无任何关系。
首先发现要删一条出边一条入边,也就是不能同时删掉两天入边和出边,那就给一个点的两条入边之间相互建边,出边同理。
建完边之后由于每个点都连出两条边,所以新的图必定是个环或者若干个环的集合。
再考虑删除,根据建边的目的,就是相邻的点我们不能选,现在看有多少种选法,从 \(2*n\) 个点中选择 \(n\) 个,并且互不相邻的方案数。
由于要这么选择,所以新的图只有是二分图的时候才合法(可以分成两个集合,每个集合内没有连边)
又因为是二分图,所以图中只有偶环,每个偶环有两种选择方案,所以最终的答案就是 \(2^t\) ,\(t\) 是环数。
这题虽然是 \(T1\) , 不过确实是我没有想到,首先就是这个建边,一般题意描述相对关系而你无从下手的时候都可以给他建个边试试看。
还有就是这个二分图性质的应用,图中只有偶环 充要 这个图是二分图。
期望的线性性
模拟79-F
首先发现这个有向图可以缩点变成 DAG ,之后我就一直认为他是 dp 最后也没做出来。
利用 期望的线性性 ,可以把他拆开,\(E(\text 删掉这张图)=\sum E(\text 删掉每个点)\)
删掉每个点的期望时间就是一次操作删掉他的概率的倒数,而一次操作删掉他的概率就是有多少个点可以到达他。
拓扑排序做可达性统计就行了,\(bitset\) 优化 \(n^3/w\) ,需要注意的是虽然点数是 \(O(n)\) 的,但是边数可以是 \(O(n^2)\) 的。
拓扑排序复杂度是 \(O(n+m)\) ,这个得注意一下,我之前一直就记了个他是线性的就没了,实际是边数多的时候复杂度就 \(n^2\) 了
还有就是看到 \(n=1000\) 可以考虑一种可能的复杂度就是 \(n^3/w\)
CF280C
和上一个题一样,这个题是问你在树上删掉一个子树的期望次数(话说树也是DAG所以做法可以照搬)
一个拆期望的套路,不过是能到达他的点就是它的深度。
模拟33-Hunter
用期望的线性性拆开,一号猎人死的期望时间就是每个人比他早死的概率。
每个猎人比他早死的概率就是 \(W_i/(W_i+W_1)\)
这种纯用线性性拆开的题,死用 dp 磕还是真磕不出来,而用线性性拆开,每次操作之间就是独立的,从而简化问题
有些题你简单的想一下看不出来他怎么拆,所以这也是期望题的一个可行思路。
猪国杀
列队春游
处理平方的套路
模拟77-联合权值?改
把题解搬过来,挺妙的对无向图三元环的应用,包括那个平方的公式和三元环最多 \(m\sqrt m\) 所以暴力第一问。
入门了一下无向图三元环计数。
把无向图定向成有向图,方向是从度数大向度数小,如果度数相等,从编号小到编号大。
这样易证新的图是有向无环的。
然后先枚举点,再枚举出边,再枚举出边的出边暴力判环。
复杂度为 \(\sum_{i}^{m} out_i\) ,\(out_i\) 代表有向图中 \(i\) 的出度,\(drgee_i\) 代表原图中 \(i\) 的度 。
证明一下 \(m\sqrt m\) 的复杂度。
若没有 \(drgee_i>\sqrt m\) ,则 任意\(i , out_i \leq \sqrt m\) 复杂度显然对。
否则,若 \(drgee_i > \sqrt m\) , 由于度数小向度数大的连边,所以他连向的点度数必定大于 \(\sqrt m\) ,这样的点只有 \(O(\sqrt m)\) 个,所以\(out_i \leq \sqrt m\) ,复杂度也是正确的。
同样可以证明一个结论,一张无向图最多有 \(m\sqrt m\) 个三元环,因为我们上述做法可以找到所有三元环,而我们最多只能找 \(m\sqrt m\) 个。
所以第一问按权值排序,找到一个合法的就退出。
如果不合法,必定是有三元环,而三元环只有 \(m\sqrt m\) 个。
第二问直接用所有答案容斥掉三元环的答案。
所有答案的形式是 \(\sum_i\sum_j a_i*a_j\) 。
对于这种需要枚举两个计算的,可以考虑这个式子 \(\sum_i\sum_j a_i*a_j=(\sum a_i)^2\)
当然有另一个形式 \(\sum_i\sum_j a_i*a_j*[a_i!=a_j]=(\sum a_i)^2-\sum (a_i)^2\)
所以直接扫出边计算就行了。
模拟48-Revive
先考虑给原式子变形。
这是经典的拆平方策略,和上面是一个操作。
第一个很好算,第二个就是枚举两条边,用 \((w_i+w_j)\) 乘上同时经过 \(i,j\)的路径条数。
开始考虑枚举一条边,直接他的贡献,只要能保证 \(log\) 复杂度就行,每次修改复杂度也就是合法的。
设这一条边是 \(a\) , 然后考虑另一条边 \(b\) , 和他的位置关系分类讨论。
- \(b\) 在 \(a\) 子树内,这个用线段树上每一个点维护一个 \(sz*w\) , 直接区间查就好了,改就是单点改 \(w\) 。
- \(b\) 在 \(a\) 到根的路径上,这个在线段树上每个点维护一个 \((n-sz)*w\) , 树剖查一条链, 单点改,然后用经典套路把树剖去掉,也就是子树修改单点查询。
- \(b\) 在 \(a\) 的其他子树内,这个我的做法比较简单,其他子树=除了 \(a\) 以外的所有子树- \(a\) 到根的链,然后用第一种情况的大小查"除了 \(a\) 以外的所有子树", \(a\) 到根的链就向第二种情况一样维护一个 \(sz*w\) 就行。
模拟43-第四题
这题难点不在 \(dp\) , 并且是一个套路,所以就放到这了。
\(f_{i,j}\) 代表前 \(i\) 个数最大值为 \(j\) 的方案数, \(g_{i,j}\) 代表放 \(i\) 个数在最大值为 \(j\) 的序列后的方案数。
然后请出 \(\rm NB\) 式子, \(\large n^2=\binom{n}{2}*2+n\) 。
这也就意味着,对于每种 \(i\) 在 \(x\) 的方案,只需要统计一遍+后面自己出现个数*2遍就行了。
枚举 \(x\) 和他出现的位置 \(i\) , 方案数就是
这个 \(\large n^2=\binom{n}{2}*2+n\) 只要题目要统计什么玩意的平方就可以考虑,然后考虑这两个同时出现的方案数。
模拟76-洛希极限
nt dp还是很简单的,直接暴力 \(n^4\) 转移。
然而观察性质可以变成 \(n^3\) , 就是转移的时候只用转移上一列/上一行的是最优的。
否则一定可以让他转移到上一列/上一行,使答案更优。
又可以发现每个点在上一列/上一行能转移的区域是单调的。
所以我们只需要求出来他最多能转移到哪里,然后就可以每行每列做单调队列转移了。
现在只需要在合法复杂度内求出来他最多能转移到哪里就可以了。
这个大部分做法复杂度是假的,正确做法应该排序之后并查集,排序完之后这一列被覆盖,之前的必定也被覆盖了。
模拟74-Sanrd
首先发现一个性质就是 LIS,LDS 交集最多为1,所以计算出来每一个位置被多少 LIS 包含.
再求一个 LDS , 如果LDS中所有位置加起来 LIS 个数等于全部 LIS 个数,那么就找不到一个和它无交集的LIS。
求出每个位置被多少包含可以直接两边分别树状数组然后在中间合并。
之后求LDS记录一下转移过来的时候两个不同的LDS数量就行了,肯定可以找到一个合法的。
思路上难点并不多,但是观察性质还是很重要的,难在实现。
模拟72-T2 最简单辣快来做
没有逆元的话,考虑四个方向分别做前缀和来动态维护。
这个是60分,100分就把格点离散化(一个大块缩成一个点)之后按这个式子做,注意边界需要特判。
又为二维静态问题提供了一个思路:四个方向分别做前缀和维护。
模拟72-T3 是我的你不要抢
暴力做复杂度是对的 (题解说对,上界 \(6e8\) ),只要记忆化下来就好了。
我们做一次匹配,复杂度是 \(min(len_a,len_b)\) 的,又由于 \(\sum len \leq 6e5\)
可以考虑根号分治证明。
若 \(len_a \leq \sqrt L ||len_b\leq \sqrt L\) , 那么复杂度是 \(\sqrt L\) , 这部分复杂度是 \(Q*\sqrt L\)
否则两个都大于,这样的字符串最多有 \(\sqrt L\) 个,都比较也没有问题。
真正的正解是AC自动机,(以下内容纯口胡)
建出来Tire树和Fail树,根据Fail树的实际意义,他就是最长能匹配的border。
所以询问就相当于匹配Fail树上1-S的链和Tire树上1-T的链最长匹配长度。
可以用一个套路,单点max查祖先链 可以树剖两个log,转化成子树max单点查,一个log
对Tire上每个节点分别做,如果我们 在 Tire 上 \(dfs\) 的话,需要用主席树+标记永久化。
但对每个串重新做一遍,这个串做完之后区间推平成0就行了。
膜拜土哥NB方法,对每个串上打时间戳,以时间为第一关键字,长度为第二关键字查询,只有查到当前时间才算合法。
模拟70-AVL
(70-AVL,https://blog.csdn.net/qq_42101694/article/details/120640655
https://blog.csdn.net/weixin_43960287/article/details/120630969),姑
模拟68-切题
邻项微扰/调整法
模拟67-数据恢复
比较好的题,下方直接放了好几道类似题,%%Amx考场切思路。
首先如果没有限制,可以用邻项交换法证明按 \(a/b\) 排序最优。
现在考虑有限制的情况,用优先队列维护,考虑取出堆顶。
若一个点father已经被选择了,那么直接选择它肯定最优。
如果没被选择,那么选完father之后选他肯定最优,所以可以把他和他父亲捆绑成一个点,并直接加上合并带来的贡献。
合并就把a,b分别相加就行了。
冲刺18-尽梨了
邻项交换容易证明按 \(\frac{a}{b+1}\) 从大到小排序是最优的。
然后我就傻了,直接按这个排序用前 \(m\) 个。。。。
分析他的含义,它的意义是当你选择这几个元素后,这样排序代价最小,而并不是这样选择最优。
看来对邻项交换还是没咋掌握,注意要结合你邻项交换的条件选择策略 , 而不是直接排序完事。
然后我就一直想按这个开 \(set\) 维护,证明了各种贪心性质。
结果,我们可以直接把原序列按这个排序,答案必定是他的一个子序列,然后 \(dp\) 优化枚举过程,就可以 \(n^2\) 。
感觉这个是邻项交换的另一个方面吧,之前都是邻项交换,排序直接选或者操作。
当邻项交换应用的是选择后按此排序最优时,但并不知道选择策略,可以考虑排完序之后 dp 选择一个子序列。
剩下的就很简单了,发现 \(a>0\) 每次至少翻倍,只用做 \(log\) 次,把 \(0\) 拎出来贪心从小选就好了。
冲刺18-七负我
两个点之间没有连边,可以调整证明一个为0不会使答案变劣。
具体方法就是保证和不变, \(x*a+y*b\rightarrow(x-T)*a+(y+T)*b\) 然后做差。
分配问题可以尝试用调整法找到一个最优策略,保持和不变是一个常用手段
所以最终分配答案的就是一个完全图。
然后就是找最大的完全图子图,折半状压也可以,也可以 \(BK\) 算法搜索。
\(BK\) 就是 \(dfs\) + 剪枝,但是需要注意的是必须找到一个使答案更优的团就立马退出。
相比于状压记录团具体是啥,他只记录团的大小,根据单调性剪枝,每次重新搜索,至于复杂度,不会证明,赵sir博客有证明(的论文)。
CSTC2007,数据备份
ACwing146
Color a tree
杂题
模拟67-古老的序列问题
模拟64-简单的字符串
首先让可以把循环同构串 \(A,B\) 拆分一下,肯定存在一种拆分方式使得 \(A=uv,B=vu\)
现在我来证明一个结论:
“ \(u\) 是 \(AB\) 的长度小于等于一半的最长 \(\rm border\) ”或者“\(v\) 是 \(BA\) 的长度小于等于一半的最长 \(\rm border\) 至少有一个为真 ”
其实等价于证明 \(u\) 不是 \(AB\) 的长度小于等于一半的最长 \(\rm border\) 的时候,\(v\) 一定是 \(BA\) 的长度小于等于一半的最长 \(\rm border\)
考虑\(u\) 不是 \(AB\) 的长度小于等于一半的最长 \(\rm border\)什么时候会发生。
当且仅当存在一个串 \(T\) , 使得 \(T\) 是 \(B\) 的 \(\rm border\) 并且 \(A+T=T+A\) 。
分类讨论 \(A\leq T\) 和 \(A>T\) ,发现一个可以表示成另一个的整周期,那么此时如果第二个也不满足,那么一定能找到一种重新的划分方式
(不想展开了,可以自己手模理解。)
所以第一种情况可以跳等差数列直接找到小于等于一半的(最多3次(两次找公差,一次跳到小于))。
第二种情况直接 \(hash\) 就可以。
虽然border理论不会,但是这个性质找的优化复杂度是真的nb,所以把题解搬过来了。
模拟63-电压机制
可以把题意转化成统计多少条边被所有奇环包含并且不被任何偶环包含。
有很多做法做着做着就成Npc了,,,
建出无向图的一颗dfs树,那么任意一条非树边都是返祖边。
其实无向图上有关环的问题都可以考虑 \(dfs\) 树。
每一个非树边都可以和树边构成一个环,根据dep差可以知道奇/偶 ,然后考虑对边差分,为他们被包含的奇/偶环加一。
其实和对点差分没什么不同,因为一条边可以被他连接的深度大的点唯一表示,所以就是减一的时候在 \(lca\) 而不是 \(fa_lca\) 而已。
模拟63-括号密码
模拟62-题目难度提升
比较 \(\rm nb\) 的题,需要大力分类讨论。
首先先来考虑最简单的做法,因为升序排序的序列一定是一种合法情况,并且是字典序最小的情况。
按位确定数字,每次选择他之后排序后面的数字看是否合法就行了。
这个做法对我们并没有任何帮助,所以先来考虑 \(a_i\) 互不相同的情况。
我们可以根据 \(a_i\) 互不相同而发现:每次加入数字,中位数必定会变化,所以中位数只能严格递增。
由此引申出一个结论,一个前缀有解当且仅当未加入的所有数字小于当前中位数。(否则加这个数进去中位数会变小)
那么分当前已经选择的集合中元素个数是奇数还是偶数讨论。
如果是奇数,那么中位数必定落在某个数上,假设是 \(m\) ,假设第一个没放进去且大于中位数的数是 \(k\) 。
因为要保证 \(k\) 放进去的时候中位数不能变小,所以如果 \((m,k)\) 中间有数,假设最靠近 \(m\) 的数是 \(t\) 。
那么放进去一个数,中位数一定会变成 \((m+t)/2\) , 并且由于 \(m\leq k,t\leq k\) ,所以中位数不会大于 \(k\),所以可以随便放一个数,肯定放最大的进去。
如果他们中间没数,那么我们放进去一个数 \(p\) , 要保证 \(m+p<=2k\) , 否则 \(k\) 加入的时候会不合法。
设 \(p=2k-m\) ,那么如果 \((m,p]\) 有数放过了,假设最靠近 \(m\) 的数是 \(z\) , 则 \(z\leq p\) ,那么下次放数中位数一定是 \((z+m)/2\leq k\) , 所以可以随便放。
如果他们中间没数,那么只能放 \((m,p]\) 中最大的数进去了。
再来考虑集合中有偶数个元素。
此时放入元素后中位数会变成一个数,要让他小于等于没放进去的所有数。
假设当前中位数是 \(m\) , 第一个没放进去的大于 \(m\) 的数是 \(k\) 。
若 \((m,k)\) 中间有数,则说明下次中位数一定会变成中间的那个数,并且小于 \(k\) , 所以可以随便放。
否则只能放 \(k\) 进去,并且下次中位数一定是 \(k\) 。
维护中位数可以用对顶堆,维护上述所有操作可以用 set \(\rm splay\)
发现之前的题解并没有写完,所以补一下。
在考虑有相同的数的情况,首先求出来所有数的中位数 \(M\) , 那么他肯定是最终序列的中位数。
如果 \(\leq M\) 的数中没有相同的数,那么说明整个中位数的函数曲线不存在斜率为0的情况,那么直接当没有重复的数就行了。
否则,找到 \(\leq M\) 的最大的重复的数,让中位数一直在他两边徘徊,也就是放一个最大的,放一个小于等于他的最大的。
直到小于等于他的全部用完,照样当算法一做,注意了,有小伙伴可能认为这个连样例二都模不过去。
实际是因为当前最大的数也可以小于M,并且发生这种情况仅当中位数的个数很多,仔细模发现也是没问题的。
模拟61-矩阵
挺好的一道构造题,可以首先考虑 \(n=2\) 时如何构造。
简单构造,不断用列操作让对角线相等,然后消掉对角线(构造方法可能很多)
更一般的情况,考虑任意一个九宫格, \(a_{1,1}+a_{2,3}+a_{3,2}-a_{1,2}-a_{2,1}-a_{3,3}\) 的值是不变的。

这是一个 3*3的正方形,无论你是用什么操作,他都能抵消掉,所以这6个数的和永远不变。
所以,有解当且仅当所有的九宫格这六个地方和都是0,当你把前两行,两列干成0之后剩下的必定全部是0。
模拟60-柱状图
首先根据单峰函数+单峰函数还是单峰函数的事实(每个拐点让斜率增加2,所以整个函数的斜率不降)
所以可以三分(不要鲁莽三分,三分之前一定要保证单峰,否则会体验CSP退役的快感。
三分之后可以开四个树状数组维护高效查询,需要离散化 \(h+i,h-i\),绝对值左边的,右边的分类讨论。
分类讨论拆绝对值很套路了,体现在二维上就是四个方向分别讨论。
模拟58- Lesson5!
考虑前后分别做拓扑排序,然后在拓扑序上枚举,答案就是 \(max(\text {前面的点的最长路},\text{后面的点的最长路},\text{前后有连边的最长路})\)
前两个正反两遍拓扑排序然后做前后缀和就行了,最后一个,考虑扫描线计算。
在当前点加入以他为起点的边,去掉以他为终点的边,然后统计答案就行了,可以拿set维护。
模拟54-表格
基础式子是枚举矩形的长和宽,看能乘下多少个矩形,每个矩形内的贡献。
每个矩形内的贡献就把一个 \(3*3\) 的看成一个格子,然后乘上 \(3*3\) 的排列数 (3!)。
发现这是一个多项式,所以可以拉格朗日直接插值,高斯消元搞出来系数来优化。
模拟52-树
很妙的一道分块题,平衡了一切换来了 \(n\sqrt{n}\)
首先需要一个根号分治。
对于 \(x\leq\sqrt{n}\) ,发现模数只有根号个,所以可以给每个模数开一个桶存深度(按 \(dfn\) 排序),每个模数的桶中会存储 \(n\) 个数。
然后再把每个模数的同分配到每个余数中,最后一共会存储 \(n\sqrt{n}\) 个数。
每次修改,直接找到对应模数,在对应余数二分定位,树状数组区间修改,一共进行 \(O(q)\) 次,如上做法每次复杂度 \(O(log n)\)。
每次查询,遍历所有模数,找到对应余数,然后树状数组单点查询,一共进行 \(O(q\sqrt{n})\) 次,如上做法每次复杂度 \(O(logn)\)。
对于 \(x>\sqrt{n}\) , 发现每次跳深度只有根号次,所以对每个深度开一个桶,一共存 \(O(n)\) 个数。
每次修改,就边跳深度边修改,一共进行 \(O(q\sqrt{n})\) 次修改,如上做法每次复杂度 \(O(logn)\)。
每次查询,直接查对应深度的桶里面单点查就行了,一共进行 \(O(q)\) 次查询,如上做法每次复杂度 \(O(logn)\)。
不难发现复杂度是不平衡的。
有一个平衡复杂度的经典操作就是序列分块。
分块区间修改区间查询是 \(O(\sqrt n)-O(\sqrt n)\)的。
但是,单点查询,区间修改是 \(O(\sqrt n) -O(1)\) 的。
如果我们进行差分,那么也可以 \(O(\sqrt n) -O(1)\) 实现区间查询单点修改。
所以对以上操作全部换成分块实现,但是发现如果每个桶一个块的话,还需要先二分定位,复杂度仍然没降下去。
所以考虑离线,每个模数,深度分开处理。
这步挺nb的,离线+序列分块平衡复杂度。
重新写题解的时候我重新思考了一下离线怎么降低复杂度,毕竟当时这步不是我自己想的。
我发现这次我想的是把离线下来的所有询问用指针扫一遍全部定位。
其实根本不用定位,直接把一整个树状数组给它就行了,因为我们是单点查询,所以并不在意区间和对不对,这步也挺nb的一个等价技巧。
模数一共有 \(\sqrt n\) 个,每个做一遍每次清空就行了。
然后发现深度的东西我们存不下(开不下 \(n\sqrt n\))的空间。
当然可以调整块长时间换空间,但是还有更nb的技巧。
当时稀里糊涂的就认为很nb,其实这么做是有道理的,他是类比了 \(\sqrt n\) 个模数,每次 \(O(n)\) 搞来的复杂度。
每根号个分成一组,处理根号次,每次重新扫一遍询问离线我们该离线的东西。
这样,把我们 \(O(n)\) 处理深度的不平衡也平衡了,而没有增加瓶颈复杂度。
这个题如果把时间空间卡严,还是很难做出来的。
尤其是分块的题,做的时候把所有操作的复杂度都列出来,看哪不平衡就搞哪,尽量避免瓶颈复杂度增加。
模拟51-万猪拱塔
神仙做法,,,每个格子的 \(w\) 各不相同,因为二维不太好枚举,考虑在权值轴上枚举。
枚举一个 \(r\) , 在线段树上记录有多少个 \(l\) 是合法的,以及合法的权值和。
把当前考虑的 \([l,r]\) 内的格子视作黑色,搞出来全部的 \((n+1)(m+1)\) 个 \(2*2\) 的正方形。
然后合法当且仅当这些小矩形中只有4个被染1个格子,没有一个被染3个格子。
维护 \([l,r]\) 内的b被染1个+被染3个的和就行了,只有4个的时候有贡献。
修改的时候,修改一个地方只有4个矩形会受到影响。
这个题不知道能获得什么,也许是当走投无路的时候构造一种可以判定的方式,尽量构造好用数据结构维护的?收货太牵强了,相当于没有。
模拟51-抑郁刀法
小数据范围考虑状压 \(dp\) , 设 \(f_{i,j}\) 代表 集合 \(i\) 染 \(j\) 种颜色的方案数。
转移考虑加入一个颜色,能给那些点染上这个颜色,要保证这些点之间没有连边。
\(dp_{i|S,t+1}+=dp_{i,t}\) , 保证 \(S\) 内无连边。
发现度为1的点可以直接删掉,并把答案乘上 \(k-1\) 就行。
发现 \(m\) 给的很卡,说明如果我们把度为 \(1,2\) 的点删掉,图中最多有 \(10\) 个点。
考虑怎么删掉度为 \(2\) 的点,度为 \(2\) 的点,等价于给两个点连一条边。
记 \(f_{a,b}\) 代表点 \(a,b\) 同色时的答案系数, \(g_{a,b}\) 代表 \(a,b\) 异色时的答案系数。
考虑重新定义状压转移式子。
初始时 \(f_{i,j}=0,g_{i,j}=1\) ,考虑删掉一个点 \(x\) ,对两边的点 \(i,j\) 造成的影响。
注意被删掉的点能选择颜色仅当他颜色未知,因为是系数所以当两边颜色已知去计算。
若已经有过贡献,根据乘法原理乘起来就行了。
这题沈队用 "集合划分" 获得 90 pts 超高分,记录一下模版。
就是钦定 \(lowbit\) 然后枚举谁跟他在一个集合,由于钦定了最小值所以不会重复。
code
inline void debug( int x ){ cout << bitset<10>(x) << endl ; }
void dfs( int x ){
if( !x ){ for( R i = 1 ; i <= top ; i ++ ) debug( st [i] ) ; puts("") ; return ; } // your operations here
int z = x & -x ;
for( R i = ( x ^ z ) ; i ; i = ( i - 1 ) & ( x ^ z ) ){ st [++ top] = i | z , dfs( x ^ ( i | z ) ) , top -- ; }
}
void sc(){
dfs( ( 1 << 5 ) - 1 ) ;
}
模拟50-第负二题
先找出来第 \(i\) 行能放下一个 \(k\) 的矩形的条件,也就是存在一个大小为 \(k\) 的菱形。
也就是对于所有的 \(i-k\leq j \leq i\) ,让中心坐标 \(y\) 满足 \(y-(k-(i-j))\leq l_j\) , 其他四个方向同理。
移一下项,发现变成了 \(y+i-k\geq l_j+j\) 那也就是直接查 \(l_j+j\) 的max是否满足就行。
至此可以二分答案+rmq算法实现一个 \(log\) 。
考虑优化二分答案,发现两行的时间差只能是 \(1,0,-1\) 。
优化 \(rmq\) 就用单调队列,原因是每次变化的查询区间并不多,但是比较不好想。
设第 \(i\) 行的答案是 \(f_i\) , 那么他的管辖范围就是 \([i-f_i+1,i]\) , \([i,i+f_i-1]\) 。
让 \(i++\) ,分别让 \(f_i \ +1 , -1\) , 不变,计算出来变化的范围,每次手动计算变化的范围。
这题算把单调队列玩的比较nb的了,主要还是的先把题目条件表示成式子移项。
然后观察出来 |1| 的性质之后扫描线的思想可以想到单调队列,但是实现也不是很简单。
模拟47-Sequence
相同的子序列问题还有,(模拟14)抛硬币,(冲刺16-传统艺能),那两个都比较模版,就不弄过来了。

\(n\leq 1e6,m\leq 1e18,k\leq 100\)
先写一下统计子序列的 \(dp\) , 设 \(f_i\) 代表以 \(i\) 结尾的子序列的个数。
转移的时候假设当前位置是字符 \(c\) , 那么 \(f_c=(\sum_i f_i)+1\) , 考虑把所有子序列后面接一个当前字符,再加上只有这一个字符的情况。
可以前缀和优化,复杂度是 \(O(n)\) 的。
往后面加 \(1e18\) 个元素,要不倍增,要不矩阵,那么首先你得找出来一个策略。
先把原序列做一遍子序列统计,那么你当前往后面放字符,可以贪心的放 \(f\) 最小的,因为下一个 \(f\) 与字符无关,所以让最小的变大肯定最优。
发现周而复始的这么做是有规律的,所以可以考虑用矩阵、倍增等优化,一次做一轮,零散的暴力做就可以了。
由于 \(dp\) 不是这题的精髓,所以就放到这了。
当无法 \(dp\) 选择策略的时候,多思考有没有贪心策略可以直接确定要选择什么。
模拟73-连边
以黑点跑多源最短路就行了,记下来需要选择的边。
模拟37-最小距离
特殊点开始跑多源最短路,如果一条边两边的端点不是一个前驱,那么就尝试用它更新答案。
一般多源最短路的题会有明显的提示,比如有两类点、特殊点等等。
当然可以自己构造出来特殊点多源最短路。
模拟36-Dove打扑克
分析不难发现,不同的牌数只有 \(O(\sqrt n)\) 种,所以操作二在二元组上双指针复杂度就是对的。
像这种总数一定的题一般都能分析出来根号复杂度,同梨还有 "模拟72-T3 是我的你不要抢",还有粉丝的根号分治基于也是这个。
所以当数据范围是 \(\sum \leq ...\) 时,可以去想总量有限等。
模拟36-Cicada 拿衣服
重要的性质:OR-AND不同的区间只有 \(log\) 段。
所以枚举一个右端点,在右端点上的 \(log\) 段区间,每一段区间都是单调的(因为MAX-MIN)单调。
所以看右端点是否合法,合法就conitnue,不合法就二分找到对应左端点(经典的log+log找决策点)。
然后考虑维护这个 \(log\) 段区间,可以拿链表维护,每次只有在0后面加1会导致多一段,1后面加0会导致少一段。
其他维护方法至少会让复杂度加一个 \(loglog\)
这道题只要看出来 \(log\) 段区间,剩下的部分就是经典扫描线。
如何看出来这个呢?一般大个鬼畜式子可能都需要找局部不变量,一般位运算操作比较多,多玩玩没准有戏。
模拟34-Merchant
发现 \(k<0\) 的函数被选中仅当答案为 0 ,否则答案有单调性,可以二分答案。
二分的时候我们知道每个元素的价值,选出最大的且大于 0 的m个,这个不需要排序,只需要 nth_element。
只需要找最大的k个而不需要关注具体值的时候,可以 nth_element
模拟82-矩形
发现如果建出笛卡尔树,那么每个节点的贡献都是等差数列。
直接二分答案,求出 \(A_l,A_r\),统计等差数列上有多少个小与他的,然后看是不是 \(L-1,R\) 就行。
具体方案用堆维护一下,每次加入等差数列上处于 \([l,r]\) 内的。
模拟22-f
首先发现逆序对可以分配到每一位上面,先用Tire处理出来每一位选择 0 / 1 情况下带来的逆序对,现在就可以 \(O(log)\) 计算 \(f(x)\) 了。
然后考虑折半,在两半分别算出来 \(f(x)\) 。
然后二分一个 \(f(res)\) 看小于他的是否是 \(p-1\) 个。
小于他的 \(f(res)\) 直接双指针扫就行了,因为cnt是可以直接加起来的。
求 \(res\) 的过程就对于每一个 \(x\) 开桶存下来 \(f(res)-x\) 的值,直接跳桶找值(搞出来所有 \(f=f(res)\) 空间不对。。。
二分答案的基本用途是最大值最小,最小值最大和求出某一个rk的值,求出某一个 \(rk\) 的值只需要二分然后看小于他的值是否有 \(rk-1\) 个就行了。
模拟32-Smooth
蚯蚓就挺smooth的,所以这个题目名字在暗示做法。
考场上直接爆搜所有合法的,复杂度 \(nlogn\)。
正解和蚯蚓是一个套路,如果我们每次取出未扩展的全局最小值进行扩展,扔到堆里面,复杂度是 \(nlogn\) 的。
但是发现如果把每个数都扩展一遍,并且只放到编号比自己大的队列里面,每个队列里面的数单调递增。
多个单调的队列循环使用=堆,注意是单调的队列,也就是你确宝这样划分队列之后,每个队列新加入的数比这个队列内所有的数都大。
模拟30-毛一琛
直接暴力枚举集合和子集是 \(3^n\) , 优化的话优先考虑折半。
把形式转化成做差,那么就是 \(A+B=C+D -> A-C=D-B\) ,这样就独立了。
在右边记录每一个 \(B|D\) 塞到对应的权值里面, 去重 , 这样每个权值最多对应 \(2^{n/2}\) 种状态。
在左边暴力枚举 \(A,C\) , 找对应的差,然后统计就行了。
折半过程中优先考虑如何独立两边,如果不能独立两边,折半就是无用的
模拟29-最近公共祖先
感觉有点思维题的感觉,就是一个小地方。
首先转化成每个点修改到根路径上的其他子树。
发现一个点被修改最多两次就能把所有子树覆盖,以后就可以直接 break 了。
然后直接搞个线段树就行,复杂度均摊。
感觉复杂度不对的时候优先想什么地方重复操作了,这个不管是优化dp还是ds都很实用
模拟28-割海成路之日
然后转化成从s出发,可以到达多少点,只不过条件变成了先经过1边,再经过3,最后经过1,2。
先来解决第一问,两个点能够相互到达,就是从t的1,2出发,从s的1出发,有个有公共点或者通过一条3边。
这个时候,在树上维护两个并查集,一个是一个点出发通过1边到达的所有点,另一个是一个点通过1,2边到达的所有点。
设第一个并查集是 fa1 , 第二个是fa2,x点的父亲是FA(x).
我们额外维护,让并查集的根是深度最小的点(或者额外维护一个并查集中深度最小的点是谁这个信息也可以)
那么,t可以到达s,当且进当满足如下条件之一。
- \(fa2(s)=fa2(t)\) 这样仅通过1,2可以到达。
- \(fa1(FA(fa2(t)))=fa1(s)\) 这样是t在s下面,通过t的1,2,跳一条边,再通过1可以互达
- \(fa2(FA(fa1(s)))=fa2(t)\) 同理,是s在t下面。
若s,t的lca不是s和t中的一个,情况2,3等价
然后比较麻烦的是第二问。
答案由两部分组成
- 直接通过1,2到达。
- 通过1,通过3后通过1,2到达。
第一种直接对第二个并查集维护size就可以了,记为size2。
第二种,需要对第一个并查集维护所有点向下,通过一个3边,能到达的2并查集size之和,记为size1。
查答案直接size1+size2+通过父亲到达的点(因为size1只维护了向下的点),(维护向上很难维护,不过也可以维护)
2变1,直接合并1的并查集就行了。
3变2,合并2的,同时对1的修改修改,这个不难讨论,就是情况不少。
然后差不多做完了,有一个实现的小技巧。
一开始把所有边都视作3边,如果这条边是1,就看做变2再变1,是2同理。
当给出的操作不用撤销并且信息可以单调合并的时候,可以考虑并查集
模拟25-string
直接枚举去匹配复杂度炸天,考虑在S中枚举分界点。
在分界点匹配两边的前后缀,暴力匹配乘起来就行,但是复杂度依旧不对。
发现题目用心良苦给你构造了可以二分答案的东西,也就是我们可以二分这个串最长匹配多少。
然后就是找有多少串是这个串的子串,这个前缀和做一下就行了。
这道题目单调性其实很明显了,一般字符串二分都会发现不能,然而这个精心的 “后缀+前缀” 绝对是枚举分界点的提示。
模拟24-graph
这道题虽然能被各种随机过掉,但是想要想到正解真的不容易。
正常的思路是 \(x\) 不同使答案可能不同的 \(x\) 不多,所以要找到合法数量的 \(x\) 。
** 考虑 \(x\) 如何取值会给答案带来不同,如果 \(1->n\) 经过了 \(k\) 条 \(x\) 边,那么其实路径已经固定了。**
这个可以用二维 spfa 求出来,设 \(f_{i,j}\) 是 \(1->n\) 经过 \(j\) 条 \(x\) 边的最短路径(x视为0) 。
那么 \(1->n\) 的路径无非 \(rnt\) 种, \(rnt\) 是 \(x\) 边的总数, \(rnt \leq m\) 。
每个 \(f_{n,j}+t*j\) 就是 \(x=j\) 时候的最短路长度,至此,我们可以计算出来 \(1->n\) 经过 \(k\) 条 \(x\) 边, \(t\) 的取值范围。
直接带入一遍 \(Dij\) , 这个是个当路径长度不唯一的时候计算路径上点的方法:
从 \(1,n\) 分别 \(dij\) , 若 \(dij[1][i]+dij[n][i]=dij[1][n]\) , 那么 \(i\) 在最短路上。
这道题的核心就在知道 \(1->n\) 的路径有 \(rnt\) 种。
模拟23-赛
枚举选择了几个两个人都喜欢的,盛夏在里面选择最小的,如果不够随意选择最小的,需要数据结构优化。
模拟22-d
优先删除 \(a,b\) 最小的,枚举删掉几个 \(a\) 最小的,剩下的删 \(b\) 最小的,需要用堆维护。
这两道贪心贪心性质比较显然,然而我在考场上都没做出来,有的贪心一共有几个方面,可以考虑枚举一个简化情况
模拟21-Game
思维妙题,只需要开一个桶维护数组中最大的数,这个指针是单调的,因为加入更大的数会被直接拿走。
模拟17-世界线
先把答案转化成到达每个点的点的个数减去边的条数,不转化每次统计也没啥问题就是常数大
然后发现可以 \(bitset\) + 拓扑排序,就是空间会爆炸。
这个时候,可以考虑分开这个 \(bitset\) ,每次只统计一个区间内的点的贡献,这样就可以重复利用 \(bitset\) 了。
空间不够用的时候考虑抽出来独立的部分,每次做互不干扰的东西,重复利用容器
模拟16-Star Way To Heaven
最大值最小,可以二分答案之后每个点搞一个圆看上下界是否联通。
然后最大值最小还可以想一个套路就是最小生成树,最大的边权就是答案。感觉可以扩展到把代价当成边?见到题再说吧。