模拟80—「邻面合并·光线追踪·百鸽笼·滑稽树下你和我」
邻面合并
每一行的状态数有限，所以可以先搜出来每一行的所有状态
转移枚举这一行的状态和上一行的状态考虑拼接，个人感觉把状态用 vector<Range> 表示比整数表示轻松。
光线追踪
其实这道题就是想到需要用角度表示就完了。
把所有询问离线下来开个线段树，直接维护每个斜率的最小的 \(x,y\) ，开两个线段树。
百鸽笼
正如题目所说，我们需要鸽掉
滑稽树下你和我
考试的时候并没有想到在边上迂回这种神器操作，于是爆炸了（幸亏我感觉这题不可能这么简单然后没写）。
所以事情从简单做起，先考虑没有边上的简单情况。
二分答案 \(mid\) ，之后开始 \(bfs\) ，定义状态 \(f_{x,y}\) 为 \(A\) 在x， \(B\) 在y是否合法。
一个状态合法的条件就是同时满足一下两条：
- 他由一个合法的状态走过来
- 满足 \(dis(x,y)\leq mid\)
每次刷表，有以下转移 , ( \(to_x\) 代表 \(x\) 能到达的点 )
- \(A,B \rightarrow to_A,B\)
- \(A,B \rightarrow A,to_B\)
- \(A,B \rightarrow to_A,to_B\)
最后直接看能否存在一个状态 \(A,B\) , 使得他们度数都是就好了。
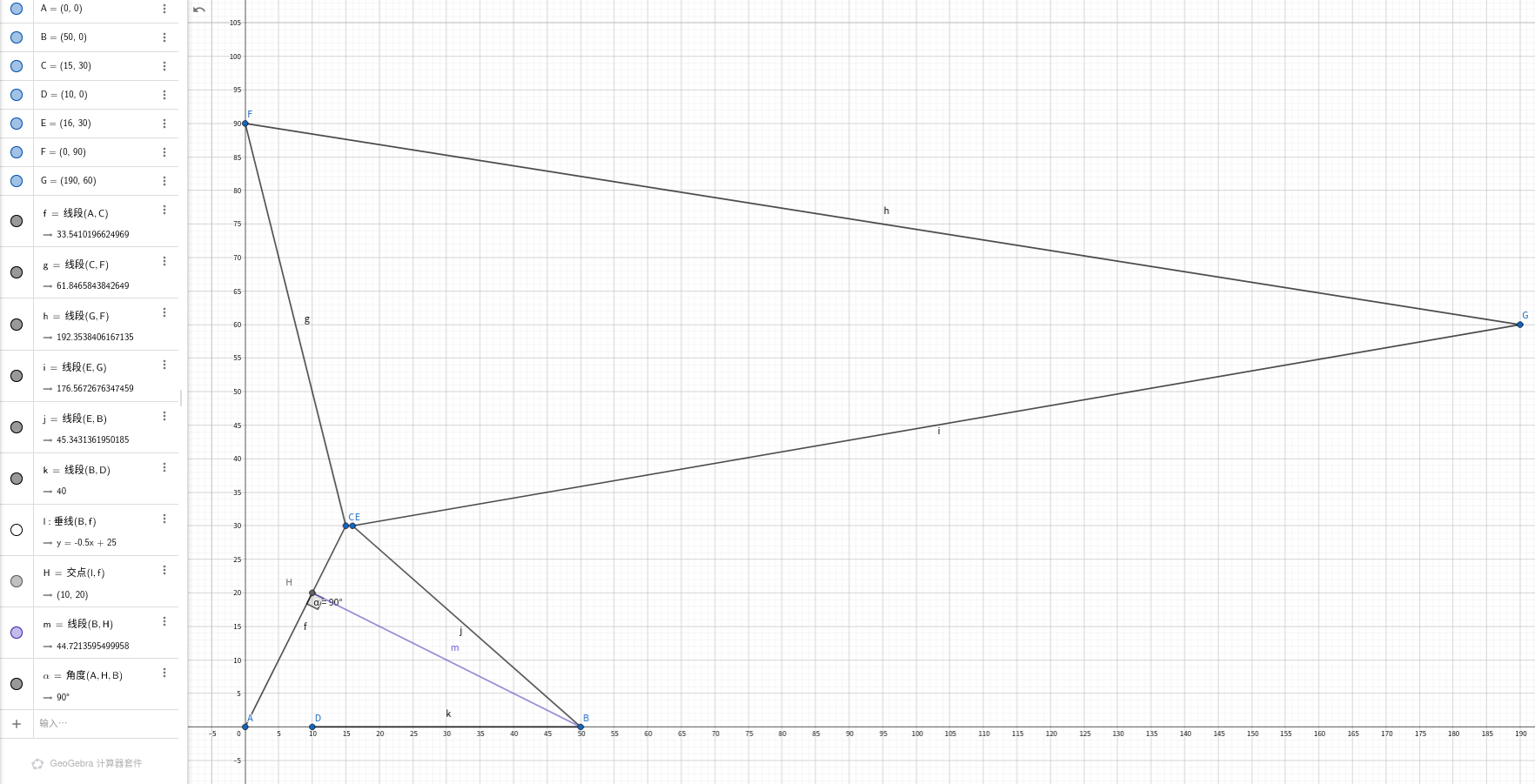
但是这个为什么不对呢？考虑以下情况( 提供样例，答案是44.721360)
7 1 5
0 0
50 0
15 30
10 0
16 30
0 90
190 60
2 4
1 3
2 5
3 6
6 7
5 7
这样构造图的原因是只让（A,E）走到（A,D）
如果朴素的走，那么我们只能让（A,E)->(A,B)->(A,D)。代价为50；
一开始，A,E有点，我们可以先让A走到H，然后让E走到B，代价为44.721360
先让B走到D，再让H回到A ，没有额外代价。
为了处理这样的情况，把边也建成一个点，让边和其两边的点连边，边和点的距离用数学知识算一算就好啦！
题解里面说有边和边的距离，我发现并没有这种情况，所以没写，也是对的，如果有人发现有这种情况，欢迎直接打脸。
总结
很爆炸的一场，T1由于不会打暴力没拍有点慌，眼动查错查到了一个 \(end\) 没判到，大概T1用了两个多小时。
想到状态数量合法之后不知道在犹豫什么，耗费了很多时间，其实果断用 \(vector\) 就完事了。
T2感觉想一会还是能想到的，但是就一个多小时了所以没什么思考了。
T4属实没想到有迂回操作，但是没开long long 所以爆0了。
所以打完 \(T1\) 之后没有拿分，其实 \(T2\) 写 60/30 ，甚至多一些思考能想到正解，但是不知道由于什么没有了开考的思考状态。
还剩下两场全真模拟，必须找到一个好点的状态了。
