【2019.8.22】测试题目订正

上午

T3：

　　

QQ截图20190821222432.png

　　上图表示了一个方阵，沿行、沿列及两个对角线的5 个数字可被当作一个5 位的质数被读入。 对于行，自左向右读数；对于列，自上向下读数；对于对角线，两个对角线 均自左向右读数。 请读入数据，编一个程序，按以下要求构成方阵。

  1. 质数中每位之和（行、列、对角线）必须相同（本例是11）。
  2. 方阵左上角中的数字预先给定（本例是1）。
  3. 若存在多个解，必须全部给出。
  4. 5 位质数中的第一个数字不能是零，例如00003 不是5 位质数。
  5. 一个5 位质数在同一方阵中可以被使用多次。

输入：

　　第1 行是质数中各位数字之和；

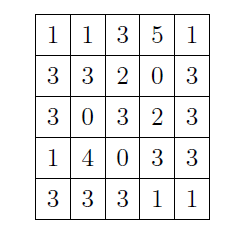
　　第2 行是方阵左上角中的数字。

　　输入文件只有2 行，保证测试数据一定有解。

　　

　　需要技巧的爆搜。尽可能早地剪掉多余状态，就需要优先枚举限制较多的状态。

　　考虑末行末列的数字必须是{1, 3, 5, 9}，那么先预处理由这几个数字构成的质数，填入最后一行和最后一列。注意到此时两条对角线的首尾已知，还可以预处理已知首尾的素数扔进对角线里。之后第2、4行和2、4列都有三位已知，因此考虑再预处理出已知第2、4、5位的质数。把这四个数填好之后，最后的两个数字已经确定了，判断是否合法即可。

　　（以下是迄今以来写过最恶心的代码……）

  1. #include <iostream>  
  2. #include <cstdio>  
  3. #include <cstring>  
  4. #include <algorithm>  
  5. #include <vector>  
  6. #define p_b push_back  
  7. #define maxn 100000  
  8. using namespace std;  
  9. void open_file(string s) {  
  10.     string In = s + ".in", Out = s + ".out";  
  11.     freopen(In.c_str(), "r", stdin);  
  12.     freopen(Out.c_str(), "w", stdout);  
  13. }  
  14. int sum, sq[6][6];  
  15. int prime[maxn];  
  16. bool del[maxn + 100], isp[10][10][10][10][10];  
  17. void euler() {//欧拉筛   
  18.     for (int i = 2; i < maxn; ++i) {  
  19.         if (!del[i]) prime[++prime[0]] = i;  
  20.         for (int j = 1; j <= prime[0] && prime[j] * i < maxn; ++j) {  
  21.             del[prime[j] * i] = true;  
  22.             if (i % prime[j] == 0) break;  
  23.         }  
  24.     }  
  25. }  
  26. vector<int> lst;  
  27. inline int get_sum(int x) {//求某数各位和，顺便预处理末行质数   
  28.     int ret = 0, cur = x;  
  29.     bool f = true;  
  30.     while (x) {  
  31.         if (!(x % 10 == 1 || x % 10 == 3 || x % 10 == 7 || x % 10 == 9)) f = false;  
  32.         ret += x % 10, x /= 10;  
  33.     }  
  34.     if (f && ret == sum) lst.p_b(cur);  
  35.     return ret;  
  36. }  
  37. vector<int> setB[10][10], setC[10][10][10];//B已知首尾，C已知2、4、5位   
  38. void init() {  
  39.     for (int i = 10000; i < maxn; ++i) {  
  40.         if (del[i] || get_sum(i) != sum) continue;  
  41.         isp[i / 10000][(i / 1000) % 10][(i / 100) % 10][(i / 10) % 10][i % 10] = true;   
  42.         //拆分质数到一个五维bool，用来判最终状态合法与否    
  43.         setB[i / 10000][i % 10].p_b(i);  
  44.         setC[(i / 1000) % 10][(i / 10) % 10][i % 10].p_b(i);  
  45.     }  
  46. }  
  47. int get_bit(int x, int bit) { //取出某个数的某一位   
  48.     for (int i = 1; i < bit; ++i)  
  49.         x /= 10;  
  50.     return x % 10;  
  51. }  
  52. inline void write(int x, int bit, int& a) { //把x的某一位写入位置a   
  53.     for (int i = 1; i < bit; ++i)  
  54.         x /= 10;  
  55.     a = x % 10;  
  56. }  
  57. bool check() { //判断答案是否合法   
  58.     int sum1 = sq[1][1] + sq[1][2] + sq[1][4] + sq[1][5];  
  59.     int sum2 = sq[2][3] + sq[3][3] + sq[4][3] + sq[5][3];  
  60.     if (sum1 != sum2) return false;//一行三列的冲突   
  61.     sq[1][3] = sum - sum1;  
  62.     if (!isp[sq[1][1]][sq[1][2]][sq[1][3]][sq[1][4]][sq[1][5]] || !isp[sq[1][3]][sq[2][3]][sq[3][3]][sq[4][3]][sq[5][3]])  
  63.         return false;//判最终写入的一个数是否满足一、3是质数   
  64.     sum1 = sq[1][1] + sq[2][1] + sq[4][1] + sq[5][1];  
  65.     sum2 = sq[3][2] + sq[3][3] + sq[3][4] + sq[3][5];  
  66.     if (sum1 != sum2) return false;//三行一列的冲突   
  67.     sq[3][1] = sum - sum1;  
  68.     if (!isp[sq[1][1]][sq[2][1]][sq[3][1]][sq[4][1]][sq[5][1]] || !isp[sq[3][1]][sq[3][2]][sq[3][3]][sq[3][4]][sq[3][5]])  
  69.         return false;  
  70.     return true;  
  71. }  
  72. struct Ans {  
  73.     int data[6][6];  
  74. } ans[1000];  
  75. bool operator < (Ans a, Ans b) {  
  76.     for (int i = 1; i <= 5; ++i)  
  77.         for (int j = 1; j <= 5; ++j)  
  78.             if (a.data[i][j] != b.data[i][j]) return a.data[i][j] < b.data[i][j];  
  79. }  
  80. int top = 0;  
  81. void add() {  
  82.     ++top;  
  83.     for (int i = 1; i <= 5; ++i)  
  84.         for (int j = 1; j <= 5; ++j)  
  85.             ans[top].data[i][j] = sq[i][j];  
  86. }  
  87. void print() {  
  88.     for (int k = 1; k <= top; ++k) {  
  89.         for (int i = 1; i <= 5; ++i) {  
  90.             for (int j = 1; j <= 5; ++j)  
  91.                 printf("%d", ans[k].data[i][j]);  
  92.             putchar('\n');  
  93.         }  
  94.         putchar('\n');  
  95.     }  
  96. }  
  97. int main() {  
  98.     open_file("prime");  
  99.     euler();  
  100.     cin >> sum >> sq[1][1];  
  101.     init();  
  102.   
  103.     for (auto i: lst)  
  104.         for (auto j: lst) {//确定最后一行和最后一列   
  105.             if (i % 10 != j % 10) continue;  
  106.             int ptr = 6, tmp = i;  
  107.             while (tmp) { //写入末行   
  108.                 sq[5][--ptr] = tmp % 10, tmp /= 10;  
  109.             }  
  110.             tmp = j, ptr = 6;  
  111.             while (tmp) { //写入末列   
  112.                 sq[--ptr][5] = tmp % 10, tmp /= 10;  
  113.             }  
  114.             for (auto k: setB[sq[1][1]][sq[5][5]]) {  
  115.                 tmp = k, ptr = 6;  
  116.                 while (tmp) { //写入对角线   
  117.                     --ptr, sq[ptr][ptr] = tmp % 10, tmp /= 10;  
  118.                 }  
  119.                 for (auto l: setB[sq[5][1]][sq[1][5]]) {  
  120.                     if (get_bit(k, 3) != get_bit(l, 3)) continue;  
  121.                     tmp = l, ptr = 6;  
  122.                     while (tmp) { //写入另一条对角线   
  123.                         --ptr, sq[6 - ptr][ptr] = tmp % 10, tmp /= 10;  
  124.                     }  
  125.                     for (auto m: setC[sq[2][2]][sq[2][4]][sq[2][5]]) { //枚举第二行   
  126.                         write(m, 5, sq[2][1]), write(m, 3, sq[2][3]);//写入   
  127.                         for (auto n: setC[sq[4][2]][sq[4][4]][sq[4][5]]) { //枚举第四行   
  128.                             write(n, 5, sq[4][1]), write(n, 3, sq[4][3]);  
  129.                             for (auto o: setC[sq[2][2]][sq[4][2]][sq[5][2]]) { //第二列   
  130.                                 write(o, 5, sq[1][2]), write(o, 3, sq[3][2]);  
  131.                                 for (auto p: setC[sq[2][4]][sq[4][4]][sq[5][4]]) { //第四列   
  132.                                     write(p, 5, sq[1][4]), write(p, 3, sq[3][4]);  
  133.                                     if (check()) add(); //判断合法，添加答案   
  134.                                 }  
  135.                             }  
  136.                         }  
  137.                     }  
  138.                 }  
  139.             }  
  140.         }  
  141.     sort(ans + 1, ans + 1 + top);//字典序   
  142.     print();  
  143.     return 0;  
  144. }  

T4：

　　有A，B两个罪犯从一条长长的街道两侧开始抢劫，街道上有很多房子，房子被染上了颜色，已知总共有n个房子，k种不同的颜色。

　　A，B两个罪犯一开始住在某两个房子里，我们并不知道具体是哪两个房子，只知道这两个房子颜色相同！

　　A从他的房子出发后向右移动并伺机抢劫，B则向左行动。现在已知A，B各打算抢劫多少个房子以及各自打算抢劫房子的颜色序列，调查了解，A，B从不抢一个颜色的房子两次，而且他俩只会一路前进不后退，最后再一个房子里汇合，完成最后一次抢劫。

　　当然，他们不会抢劫一开始住的房子。

　　你的任务是计算出他们可能在哪些房子汇合，以便协助警方实施抓捕。

　　n <= 1e6

 

下午

T1：

　　小明是一名教官，他正在执教n个学员。学员从左到右排成一排，编号为1~n，每个学员都有一个独一无二的身高Hi，小明想把学员们从矮到高排好序。他排序的方法是：每一次将所有的人划分为尽量少的连续部分，使得每一部分的人的高度都是单调下降，然后将其中所有不少于2 个人的区间全部翻转。重复执行以上操作，最后使得所有人的高度全部单调上升。 小明在划分并翻转完第一次之后，觉得这个工作可能过于繁琐，所以他想找你帮他计算，他一共要执行多少次翻转操作才能把所有人排好序，如果太麻烦他就要调整方案。 巧合的是，他第一次划分出来的所有区间的长度都是偶数。

　　n <= 1e5

　　

　　题中给出了一个暗示：小明在翻转第一轮之后发现了麻烦。这实际上是因为第一次翻转之后序列变成了若干个连续单调上升区间，在这之后只有这些区间的交界处可能满足一个逆序关系。这样，之后的操作就全部变成了同冒泡排序一样的两两交换。考虑此时序列中的一个数x：当且仅当x前面的一个数比它大的时候会被交换一次，而因为每次只能交换两个相邻的数，x必然会与它前面的每个更大的数都相遇一次。也就是说，第一次翻转之后的序列中的“每个数会被交换的次数”是它之前比它大的数的个数，那么总的答案就是第一次翻转的次数加上当前序列的逆序对个数。

代码：

  1. #include <iostream>    
  2. #include <cstring>    
  3. #include <cstdio>    
  4. #define BUG puts("$$$")    
  5. #define maxn 100010    
  6. using namespace std;    
  7. void open_file(string s) {    
  8.     string In = s + ".in", Out = s + ".out";    
  9.     freopen(In.c_str(), "r", stdin);    
  10.     freopen(Out.c_str(), "w", stdout);    
  11. }    
  12. template <class T>    
  13. void read(T &x) {    
  14.     x = 0;    
  15.     int f = 1;    
  16.     char ch = getchar();    
  17.     while (!isdigit(ch)) {    
  18.         if (ch == '-')    
  19.             f = -1;    
  20.         ch = getchar();    
  21.     }    
  22.     while (isdigit(ch)) {    
  23.         x = x * 10 + (ch ^ 48);    
  24.         ch = getchar();    
  25.     }    
  26.     x *= f;    
  27. }    
  28. int a[maxn], b[maxn];    
  29. int n;    
  30. int bit[maxn];    
  31. inline int lowbit(int x) { return x & (-x); }    
  32. void modify(int x) {    
  33.     while (x <= n) ++bit[x], x += lowbit(x);    
  34. }    
  35. int query(int x) {    
  36.     int sum = 0;    
  37.     while (x) sum += bit[x], x -= lowbit(x);    
  38.     return sum;    
  39. }    
  40. int main() {    
  41.     open_file("instructor");    
  42.     read(n);    
  43.     for (int i = 1; i <= n; ++i) read(b[i]);    
  44.     //  b[n + 1] = -1;    
  45.     long long ans = 0;    
  46.     for (int i = 1; i <= n; ++i) {    
  47.         int cur = i;    
  48.         while (b[i + 1] < b[i] && i < n) ++i;    
  49.         for (int j = cur; j <= i; ++j) {  // BUG;    
  50.             a[j] = b[cur + i - j];    
  51.         }    
  52.         ++ans;    
  53.     }    
  54.     for (int i = n; i; --i) {    
  55.         ans += query(a[i]);    
  56.         modify(a[i]);    
  57.     }    
  58.     printf("%lld", ans);    
  59. }    

T2：

　　定义f(x) = sqrt(x)，f_1(x) = f(x)，f_y(x) = f(f_(y-1)(x))，给定一个数n，找出使得f_y(x) = 1的最小的y。特别地，若y大于等于6时输出“TAT”。

 

　　第一想法高精度乘法 + 二分，然而不会高精度乘法。花了一个半小时钻研python怎么写……最后语法对了，死在了特判上。

　　先放python代码，特判0和1的情况即可。

  1. from math import *    
  2. f = open("sqrt.in", mode = "r");    
  3. k = open("sqrt.out", mode = "w")    
  4. que = f.readlines()    
  5. que = [int(x) for x in que]    
  6. f.close()    
  7. for a in que:    
  8.     if a == 0:    
  9.         print >> k, 'TAT';    
  10.         continue;    
  11.     if (a == 1):    
  12.         print >> k, '0';    
  13.         continue;    
  14.     f = 0;    
  15.     for i in range (1, 6):    
  16.         a = int(sqrt(a));    
  17.         if a == 1:    
  18.             print >> k, i;    
  19.             f = 1;    
  20.             break;    
  21.     if (f == 0) :    
  22.         print >> k, 'TAT';    
  23. k.close()    

　　实际上并不用写高精度。因为最多开5遍根号，那么满足条件的最大整数应是2^(2^5) - 1 = 2^32 - 1，刚好是unsigned int的最大值。用字符串读入给定数据，若数据大于2^32 - 1直接输出"TAT"，否则暴力二分开根就好了。本来听郝巨说完正解后打了C++，然而没有特判1……

代码：

  1. #include <iostream>    
  2. #include <cstdio>    
  3. #include <cstring>    
  4. #include <cmath>    
  5. #define ul unsigned int    
  6. #define BUG puts("$$$")    
  7. using namespace std;    
  8. char s[111], maxs[111];    
  9. int main() {    
  10.     freopen("sqrt.in", "r", stdin);    
  11.     freopen("sqrt.out", "w", stdout);    
  12.     ul a;    
  13.     a = (ul)(1) << 31;    
  14.     a -= 1, a *= 2, a += 1;    
  15.     for (int i = 9; i >= 0; --i) {    
  16.         maxs[i] = (a % 10) + 48;    
  17.         a /= 10;    
  18.     }    
  19.     while (scanf("%s", s) != EOF) {    
  20.         int len = strlen(s);    
  21.         if (len > 10 || (len == 1) && (s[0] == '0')) {    
  22.             puts("TAT");    
  23.             continue;    
  24.         } else if (len == 10 && strcmp(s, maxs) > 0) {    
  25.             puts("TAT");    
  26.             continue;    
  27.         }    
  28.         if ((len == 1) && s[0] == '1') {    
  29.             puts("0");    
  30.             continue;    
  31.         }    
  32.         a = 0;    
  33.         for (int i = 0; i < len; ++i) a = a * 10 + (s[i] ^ 48);    
  34.         for (int i = 1; i < 6; ++i) {    
  35.             a = sqrt(a);    
  36.             if (a == 1) {    
  37.                 printf("%d\n", i);    
  38.                 break;    
  39.             }    
  40.         }    
  41.     }    
  42.     return 0;    
  43. }   
posted @ 2019-08-22 20:47  onyYuan  阅读(243)  评论(0)  编辑  收藏  举报