二叉搜索树

二叉树搜索树

二叉搜索树：一颗二叉树可以为空：如果不为空，满足以下性质：

1.非空左子树的所有值小于根节点的键值

2.非空右子树的所有值大于根节点的键值

3.左右子树都是二叉搜索树

 

 

查找：1.查找关键之2.查找最值

对于遇到的每个结点x，都会比较x.key与k的大小，如果相等，就终止查找，否则，决定是继续往左子树还是右子树查找。因此，整个查找过程就是从根节点开始一直向下的一条路径，若假设树的高度是h，那么查找过程的时间复杂度就是O(h)。

递归做法：

　　Pision Find(elementType x,Pision binTree bst) 
　　{
　　    if(!bst)//空树 
　　        return NULL
　　    if(x>bst->data)//去右子树中查找 
　　        return Find(x,bst->right);
　　    else if(x<bst->data)//去左子树中查找 
　　        return Find(x,bst->Left)
　　    else //找到 
　　        return bst;
　　}

此递归为尾递归，递归效率并不高，一般尾递归都可以用循环表示：

　　Pision Find(elementType x,Pision binTree bst) 
　　{
　　    while(bst)
　　    {
　　        if(x>bst->data)//去右子树中查找 
　　            bst=bst->right);
　　        else if(x<bst->data)//去左子树中查找 
　　            bst=x,bst->Left;
　　        else //找到 
　　        return bst;
　　    }
　　    return NULL;
　　}

最大元素一定是在树的最右分支的端结点上（一定没有右儿子）

最小元素一定是在树的最左分支的端结点上（一定没有左儿子）

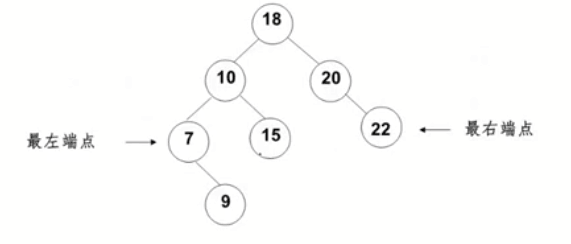
递归做法：

　　Pision FindMin(binTree bst) 
　　{
　　    if(!bst)
　　        return NULL
　　    else if(!bst->Left)
　　        return bst->Left
　　    else FindMin(bst);
　　    return bst;
　　}
　　Pision FindMax(binTree bst) 
　　{
　　    if(!bst)
　　        return NULL
　　    else if(!bst->Right)
　　        return bst->Right
　　    else FindMax(bst);
　　    return bst;
　　}

迭代做法：

　　Pision FindMin(binTree bst) 
　　{
　　    if(bst)
　　    {
　　        while(bst->Left)
　　        bst=bst->Left;
　　    }
　　    return bst;
　　}
　　Pision FindMax(binTree bst) 
　　{
　　    if(bst)
　　    {
　　        while(bst->Right)
　　        bst=bst->Right;
　　    }
　　    return bst;
　　}

插入

（关键是找到应该插入的位置）

BST的插入过程非常简单，很类似与二叉树搜索树的查找过程。当需要插入一个新结点时，从根节点开始，迭代或者递归向下移动，直到遇到一个空的指针NILL，需要插入的值即被存储在该结点位置。

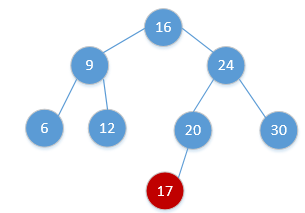
递归做法：

binTree insert( elemenType x,binTree bst) 
{
    if(!bst)
    {
        bst=(binTree)malloc(sizeof(treeNode));
        bst->data=x;
        bst->Left=bst->Right=NULL;
    }
    else
    {
        if(x<bst->data)
        {
            bst->Left=insert(x,bst->Left);
        }
        else if(x>bst->Right)
        {
            bst->Right=insert(x,bst->Right);
        }
        //如果x已经存在，则什么都不做 
    }
    return bst;
}

迭代做法：

void insert( elemenType x,binTree bst) 
{
    binTree p=(binTree)malloc(sizeof(treeNode));
    binTree temp=NULL;
    p->data=x;
    p->Left=p->Right=NULL;
    if(!bst)
    {
        bst=p;
        return ;
    }
    while(bst)
    {
        temp=bst;
        if(x>bst->data)
            bst=bst->Right
        else if(x<bst->data)
            bst=bst->Left;
        else
            return ; 
    }
    if(p->data>temp->data)
        temp->Right=p;
    else if(p->data<temp->data)
        temp->Left=p;
}

删除

二叉搜索树的结点删除比插入较为复杂，总体来说，结点的删除可归结为三种情况：

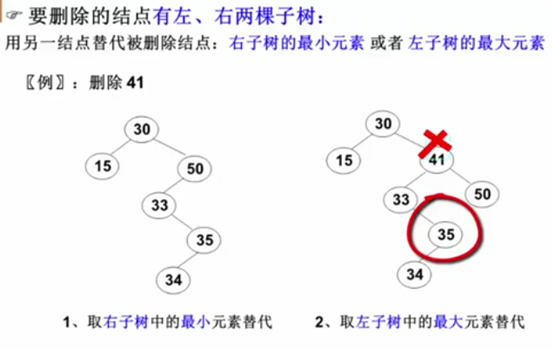
因为左子树的最大值和右子树的最小值一定不会有两个结点

递归方法：

binTree Delete(elementype x,binsTree bst)
{
    binTree temp;
    if(!bst) printf("没找到");
    else if(x<bst->data)
        bst->Left=Delete(x,bst->Left);//左子树递归删除 
    else if(x>bst->data)
        bst->Right=Delete(x,bst->Right);//右子树递归删除 
    else//找到要删除的结点 
    {
        if(bst->Left&&bst->Right)//该删除的结点有左右孩子 
        {
            temp=FindMin(bst->Right);//去右子树中找最小值代替该删除结点 
            bst->data=temp->data;
            bst->Right=Delete(bst->data,bst->Right);//在右子树中删除最小值 
        }
        else
        {
            if(!bst->Left&&!bst->Left)//无孩子结点 
            {
                free(bst);
                return NULL;
            }
            temp=bst;
            if(!bst->Left)//无左子树 
                bst=bst->Right;
            else(!bst->Right)//无右子树 
                bst=bst->Left;
            free(temp);
        }
    }
    return bst;
}     

 二插搜索树的调整：

未完