堆排序

一、堆排序算法的基本特性
时间复杂度：O(nlgn)...
//等同于归并排序
最坏：O(nlgn)
空间复杂度：O(1).
不稳定。

 

二、堆与最大堆的建立
要介绍堆排序算法，咱们得先从介绍堆开始，然后到建立最大堆，最后才讲到堆排序算法。

2.1、堆的介绍
    如下图，

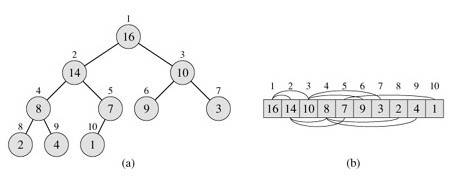
a），就是一个堆，它可以被视为一棵完全二叉树。
每个堆对应于一个数组b），假设一个堆的数组A，
我们用length[A]表述数组中的元素个数，heap-size[A]表示本身存放在A中的堆的元素个数。
当然，就有，heap-size[A]<=length[A]。

    树的根为A[1]，i表示某一结点的下标，
则父结点为PARENT(i)，左儿子LEFT[i]，右儿子RIGHT[i]的关系如下：

PARENT(i)
   return |_i/2_|

LEFT(i)
   return 2i

RIGHT(i)
   return 2i + 1

    二叉堆根据根结点与其子结点的大小比较关系，分为最大堆和最小堆。
最大堆：
根以外的每个结点i都不大于其根结点，即根为最大元素，在顶端，有
     A[PARENT(i)] （根）≥ A[i] ,

最小堆：
根以外的每个结点i都不小于其根结点，即根为最小元素，在顶端，有
     A[PARENT(i)] （根）≤ A[i] .

在本节的堆排序算法中，我们采用的是最大堆；最小堆，通常在构造最小优先队列时使用。

    由前面，可知，堆可以看成一棵树，所以，堆的高度，即为树的高度，O(lgn)。
所以，一般的操作，运行时间都是为O(lgn)。

具体，如下：
The MAX-HEAPIFY：O(lgn)  这是保持最大堆的关键.
The BUILD-MAX-HEAP:线性时间。在无序输入数组基础上构造最大堆。
The HEAPSORT：O(nlgn) time, 堆排序算法是对一个数组原地进行排序.
The MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, HEAP-MAXIMUM：O(lgn)。
可以让堆作为最小优先队列使用。 

算法实现：

堆的存储结构：

typedef struct HeapStruct
{
    int *elements;//存储堆元素的数组 
    int size; //当前堆中元素的个数 
    int capacity;//堆的最大容量 
}MaxHeap;

插入：将新插入的元素放在最后位置，与其父节点比较，如果大于父节点则交换；

删除：取最大结点（根节点，下标为一），然后将最后的叶结点放置在根节点，与左右孩子比较，如果小于较大的孩子结点则交换。

建立堆：1.依次调用插入函数，效率不高。

　　　　2.先顺序存放元素，然后将整个堆分为各各小堆，从最后的小堆开始调整，直至整个堆调整完毕，调整方法与删除方法相同。

整体代码实现：

#include<stdio.h>
#include<stdlib.h>
#define MaxData 10000
typedef struct HeapStruct
{
    int *elements;//存储堆元素的数组 
    int size; //当前堆中元素的个数 
    int capacity;//堆的最大容量 
}MaxHeap;
MaxHeap *creat(int MaxSize)//常见最大容量为MaxSize的空的最大堆 
{
    MaxHeap * H=(MaxHeap *)malloc(sizeof(struct HeapStruct));
    H->elements=(int *)malloc(sizeof(int)*MaxSize+1);// 从下标1开始存放 
    H->size=0;
    H->capacity=MaxSize;
    H->elements[0]=MaxData;
    return H;//定义哨兵为大于堆中所有可能的元素，便于以后更快操作 
}
void Insert(MaxHeap *H,int item)
{
    int i;
    if(H->size==H->capacity)
    {
        printf("最大堆已满\n");
        return ;
    }
    i=++H->size;//i指向堆中最后一个元素的位置 
    for( ;item>H->elements[i/2];i=i/2)//与父亲结点比较，向下过滤 ,其中element[0]为哨兵，不小于最大元素，防止越界 
        H->elements[i]=H->elements[i/2];
    H->elements[i]=item;//将item插入 
}
int DeleteMax(MaxHeap *H)
{
    int parent,child;
    int max,temp;
    if(H->size==0 )
    {
        printf("堆为空");
        return ;
    }
    max=H->elements[1];
    temp=H->elements[(H->size)--];
    for(parent=1;parent*2<=H->size;parent=child)//parent<=H->size判断有没有左儿子，如果左儿子都没有，右儿子不可能有 
    {
        child=parent*2;//child指向左儿子 
        if(child!=H->size&&H->elements[child]<H->elements[child+1])//child!=H->size如果不是最后一个，说明存在右儿子 
            child++; //child指向左右孩子中较大的
        if(temp>=H->elements[child])
            break;
        else
            H->elements[parent]=H->elements[child]; 
    }
    H->elements[parent]=temp;
    return max; 
}
MaxHeap* CreatHeap(void)//分割成许多小堆，从最后一个小堆，依次向前调整 
{
    MaxHeap *H=creat(500);
    while(1)
    {
        int temp;
        printf("请输入数据(-1结束);\n");
        scanf("%d",&temp);
        if(temp==-1)
            break;
        else
            H->elements[++H->size]=temp;
    }
    int parent,child,temp,n;
    n=H->size/2;//指向最后一个有孩子的父结点 
    while(n>0)
    {
        parent=n; 
        temp=H->elements[parent];
        for( ;parent*2<=H->size;parent=child)
        {
            child=parent*2;//child指向左儿子 
            if(child!=H->size&&H->elements[child]<H->elements[child+1])
                child++; 
            if(temp>=H->elements[child])
                break;
            else
                H->elements[parent]=H->elements[child]; 
        }
        H->elements[parent]=temp;
        n--;
    }
    return H;
 } 
int main()
{
    MaxHeap *H=CreatHeap();
    int i; 
　　scanf("%d",&i);
    Insert(H,i);
    while(H->size!=0)
    {
        int i=DeleteMax(H);
        printf("%4d",i);
    }
    return 0;
}

常见应用：优先队列