历届试题 九宫重排/八数码问题
历届试题 九宫重排
时间限制:1.0s 内存限制:256.0MB
问题描述
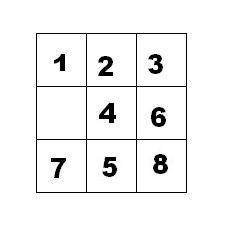
如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
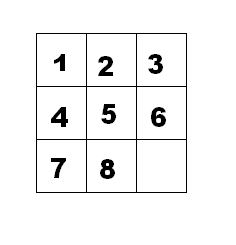
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
输入格式
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出格式
输出最少的步数,如果不存在方案,则输出-1。
样例输入
12345678.
123.46758
123.46758
样例输出
3
样例输入
13524678.
46758123.
46758123.
样例输出
22
自己的基础知识一点都不牢固!是不是该考虑从头开始学了。
#include <iostream> #include <cstdio> #include <vector> #include <queue> #include <map> #include <stack> #include <cstring> #include <algorithm> #include <cstdlib> #define FOR(i,x,n) for(long i=x;i<n;i++) #define ll long long int #define INF 0x3f3f3f3f #define MOD 1000000007 #define MAX_N 50005 using namespace std; struct node{ int x,y; int previousX,previousY;//DD¨¢D int nine[3][3]; int step; }; char t1[10]; char t2[10]; queue<node> st; int dirX[4]={-1,1,0,0}; int dirY[4]={0,0,-1,1}; node init; node finall; map<int,int> ma; bool check(node a){ FOR(i,0,3){ FOR(j,0,3){ if(a.nine[i][j]!=finall.nine[i][j]){ return false; } } } return true; } int cal(node n){ int a=0; FOR(i,0,3){ FOR(j,0,3){ a=a*10+n.nine[i][j]; } } return a; } int dfs(){ while(!st.empty()){ node now=st.front();st.pop(); int t=cal(now); if(ma[t]!=0){ continue; } ma[t]++; if(check(now)){ return now.step; } if(now.step==100){ return -1; } FOR(i,0,4){ node next=now; next.x+=dirX[i]; next.y+=dirY[i]; if(next.x>=0&&next.x<=2&&next.y>=0&&next.y<=2&&!(next.x==next.previousX&&next.y==next.previousY)){ next.nine[now.x][now.y]=next.nine[next.x][next.y]; next.nine[next.x][next.y]=0; next.step++; next.previousX=now.x; next.previousY=now.y; st.push(next); } } } } int main() { //freopen("data.txt", "r", stdin); //freopen("data.out", "w", stdout); //fill(use,use+100000,'0'); scanf("%s",t1); scanf("%s",t2); init.step=0; FOR(i,0,9){ if(t1[i]=='.'){ init.previousX=i/3; init.previousY=i%3; init.x=init.previousX; init.y=init.previousY; init.nine[i/3][i%3]=0; }else{ init.nine[i/3][i%3]=t1[i]-'0'; } } finall.step=0; FOR(i,0,9){ if(t2[i]=='.'){ finall.previousX=i/3; finall.previousY=i%3; finall.x=finall.previousX; finall.y=finall.previousY; finall.nine[i/3][i%3]=0; }else{ finall.nine[i/3][i%3]=t2[i]-'0'; } } st.push(init); printf("%d\n",dfs()); //fclose(stdin); //fclose(stdout); return 0; }



