codeforces_Codeforces Round #541 (Div. 2)_abc

A. Sea Battle

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

In order to make the "Sea Battle" game more interesting, Boris decided to add a new ship type to it. The ship consists of two rectangles. The first rectangle has a width of w1w1 and a height of h1h1, while the second rectangle has a width of w2w2 and a height of h2h2, where w1≥w2w1≥w2. In this game, exactly one ship is used, made up of two rectangles. There are no other ships on the field.

The rectangles are placed on field in the following way:

• the second rectangle is on top the first rectangle;
• they are aligned to the left, i.e. their left sides are on the same line;
• the rectangles are adjacent to each other without a gap.

See the pictures in the notes: the first rectangle is colored red, the second rectangle is colored blue.

Formally, let's introduce a coordinate system. Then, the leftmost bottom cell of the first rectangle has coordinates (1,1)(1,1), the rightmost top cell of the first rectangle has coordinates (w1,h1)(w1,h1), the leftmost bottom cell of the second rectangle has coordinates (1,h1+1)(1,h1+1) and the rightmost top cell of the second rectangle has coordinates (w2,h1+h2)(w2,h1+h2).

After the ship is completely destroyed, all cells neighboring by side or a corner with the ship are marked. Of course, only cells, which don't belong to the ship are marked. On the pictures in the notes such cells are colored green.

Find out how many cells should be marked after the ship is destroyed. The field of the game is infinite in any direction.

Input

Four lines contain integers w1,h1,w2w1,h1,w2 and h2h2 (1≤w1,h1,w2,h2≤1081≤w1,h1,w2,h2≤108, w1≥w2w1≥w2) — the width of the first rectangle, the height of the first rectangle, the width of the second rectangle and the height of the second rectangle. You can't rotate the rectangles.

Output

Print exactly one integer — the number of cells, which should be marked after the ship is destroyed.

Examples

input

Copy

2 1 2 1

output

Copy

12

input

Copy

2 2 1 2

output

Copy

16

Note

In the first example the field looks as follows (the first rectangle is red, the second rectangle is blue, green shows the marked squares):

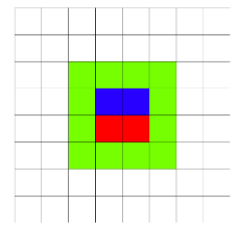
In the second example the field looks as:

 思路：有两个长方形，都是左对齐，一个摆放在另一个上面，求相邻的绿色格子有多少个。

要注意上下长方形的宽度不同的时候、拐角处的格子。

#include <iostream>
#include <cstdio>

using namespace std;

int main()
{
    long long w1,h1,w2,h2;
    while(~scanf("%I64d %I64d %I64d %I64d",&w1,&h1,&w2,&h2)){
        if(w2==w1){
            printf("%I64d\n",w1+w2+4+(h1+h2)*2);
        }else{
            printf("%I64d\n",w1+w2+4+(h1+h2)*2+(w1-w2));
        }

    }
    return 0;
}

B. Draw!

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You still have partial information about the score during the historic football match. You are given a set of pairs (ai,bi)(ai,bi), indicating that at some point during the match the score was "aiai: bibi". It is known that if the current score is «xx:yy», then after the goal it will change to "x+1x+1:yy" or "xx:y+1y+1". What is the largest number of times a draw could appear on the scoreboard?

The pairs "aiai:bibi" are given in chronological order (time increases), but you are given score only for some moments of time. The last pair corresponds to the end of the match.

Input

The first line contains a single integer nn (1≤n≤100001≤n≤10000) — the number of known moments in the match.

Each of the next nn lines contains integers aiai and bibi (0≤ai,bi≤1090≤ai,bi≤109), denoting the score of the match at that moment (that is, the number of goals by the first team and the number of goals by the second team).

All moments are given in chronological order, that is, sequences xixi and yjyj are non-decreasing. The last score denotes the final result of the match.

Output

Print the maximum number of moments of time, during which the score was a draw. The starting moment of the match (with a score 0:0) is also counted.

Examples

input

Copy

3
2 0
3 1
3 4

output

Copy

2

input

Copy

3
0 0
0 0
0 0

output

Copy

1

input

Copy

1
5 4

output

Copy

5

Note

In the example one of the possible score sequences leading to the maximum number of draws is as follows: 0:0, 1:0, 2:0, 2:1, 3:1, 3:2, 3:3, 3:4.

题意：给出几个比赛时的分数，求这场比赛中最多可以有多少个平局的状态。

可以挨着算，第一个状态肯定是0:0，然后算第一个比分跟0:0之间有多少个，再第二个跟第一个之间，依次类推。

要注意上一个的比分是平局的时候，就不再+1了，因为上一个的计算中已经算进去了。

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int main()
{
    int n;
    int a,b;
    int res=1;
    int la=0,lb=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d %d",&a,&b);
        if(a==la&&b==lb&&i!=1){
            continue;
        }
        int tmp=min(a,b);
        int tmp2=max(la,lb);
        if(tmp2>tmp){
        }else{
            if(la!=lb){
                res+=(tmp-tmp2+1);
            }else{
                res+=(tmp-tmp2);
            }

        }
        la=a,lb=b;
    }
    printf("%d\n",res);
    return 0;
}

C. Birthday

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Cowboy Vlad has a birthday today! There are nn children who came to the celebration. In order to greet Vlad, the children decided to form a circle around him. Among the children who came, there are both tall and low, so if they stand in a circle arbitrarily, it may turn out, that there is a tall and low child standing next to each other, and it will be difficult for them to hold hands. Therefore, children want to stand in a circle so that the maximum difference between the growth of two neighboring children would be minimal possible.

Formally, let's number children from 11 to nn in a circle order, that is, for every ii child with number ii will stand next to the child with number i+1i+1, also the child with number 11 stands next to the child with number nn. Then we will call the discomfort of the circle the maximum absolute difference of heights of the children, who stand next to each other.

Please help children to find out how they should reorder themselves, so that the resulting discomfort is smallest possible.

Input

The first line contains a single integer nn (2≤n≤1002≤n≤100) — the number of the children who came to the cowboy Vlad's birthday.

The second line contains integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) denoting heights of every child.

Output

Print exactly nn integers — heights of the children in the order in which they should stand in a circle. You can start printing a circle with any child.

If there are multiple possible answers, print any of them.

Examples

input

Copy

5
2 1 1 3 2

output

Copy

1 2 3 2 1

input

Copy

3
30 10 20

output

Copy

10 20 30

Note

In the first example, the discomfort of the circle is equal to 11, since the corresponding absolute differences are 11, 11, 11 and 00. Note, that sequences [2,3,2,1,1][2,3,2,1,1] and [3,2,1,1,2][3,2,1,1,2] form the same circles and differ only by the selection of the starting point.

In the second example, the discomfort of the circle is equal to 2020, since the absolute difference of 1010 and 3030 is equal to 2020.

题意：一串数字，让他们围成圈，求一个“不舒服的值”最小的情况，这个不舒服的值是每个数字之间差的绝对值的最大值。

排序，然后正着取奇数位，倒着取偶数位。

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int main()
{
    int n;
    int a[105];
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    sort(a,a+n);
    printf("%d",a[0]);
    if(n%2==0){
        for(int i=2;i<n-1;i++,i++){
            printf(" %d",a[i]);
        }
        for(int i=n-1;i>=1;i--,i--){
            printf(" %d",a[i]);
        }
    }else{
        for(int i=2;i<n;i++,i++){
            printf(" %d",a[i]);
        }
        for(int i=n-2;i>=1;i--,i--){
            printf(" %d",a[i]);
        }
    }
    printf("\n");
    return 0;
}