NOIP2015提高组复赛Day1Day2详解
T1:填幻方

这道题目非常水,直接按照题目里说的做就行了
其实机智的你们可以直接跳过题面直接开始做

1 #include <cstdio> 2 #include <cstring> 3 int a[100][100]; 4 int main() 5 { 6 int n; 7 memset(a,0,sizeof(a)); 8 scanf("%d",&n); 9 int num=1; 10 int i,j; 11 i=1; j=n/2+1; 12 a[i][j]=1; 13 while (num<=n*n) 14 { 15 num++; 16 i--; j++; 17 if (i<1 && j<=n) 18 { 19 i=n; 20 } 21 else if (i<1 && j>n) 22 { 23 i++; i++; j--; 24 } 25 else if (j>n) 26 { 27 j=1; 28 } 29 else if (a[i][j]!=0) 30 { 31 i++; 32 j--; 33 i++; 34 } 35 a[i][j]=num; 36 /*for (int i=1; i<=n; i++) 37 { 38 for (int j=1; j<=n; j++) 39 printf("%d ",a[i][j]); 40 printf("\n"); 41 }*/ 42 } 43 for (i=1;i<=n; i++) 44 { 45 for (j=1; j<=n-1; j++) 46 printf("%d ",a[i][j]); 47 printf("%d\n",a[i][n]); 48 } 49 }
T2:信息传递
题目描述
有 n个同学(编号为 1 到 n)正在玩一个信息传递的游戏。在游戏里每人都有一个
固定的信息传递对象,其中,编号为 i的同学的信息传递对象是编号为Ti的同学。 游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前
所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自 己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入
输入共 2 行。
第 1 行包含 1 个正整数第 1 行包含 1 个正整数 n,表示 n 个人。
第 2 行包含
输出
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
样例输入
样例输出

1 #include <cstdio> 2 #include <queue> 3 #include <cstring> 4 using namespace std; 5 queue <int> q; 6 int f[200001]; int flag[200001]; int e[200001]; 7 int main() 8 { 9 memset(flag,0,sizeof(flag)); 10 int n; 11 scanf("%d",&n); 12 for (int i=1; i<=n; i++) 13 { 14 scanf("%d",&f[i]); 15 e[f[i]]++; 16 } 17 for (int i=1; i<=n; i++) 18 { 19 if (e[i]==0) 20 { 21 q.push(i); 22 flag[i]=1; 23 } 24 } 25 while (! q.empty()) 26 { 27 int now=q.front(); 28 q.pop(); 29 --e[f[now]]; 30 if (e[f[now]]==0) 31 { 32 flag[f[now]]=1; 33 q.push(f[now]); 34 } 35 } 36 int ans=1000000000; 37 for (int i=1; i<=n; i++) 38 { 39 if (e[i] !=0 && flag[i]==0) 40 { 41 flag[i]=1; 42 int j=f[i]; 43 int tmp=1; 44 while (flag[j]==0) 45 { 46 flag[j]=1; 47 j=f[j]; 48 tmp++; 49 } 50 if (tmp<=ans) ans=tmp; 51 } 52 } 53 printf("%d\n",ans); 54 return 0; 55 }
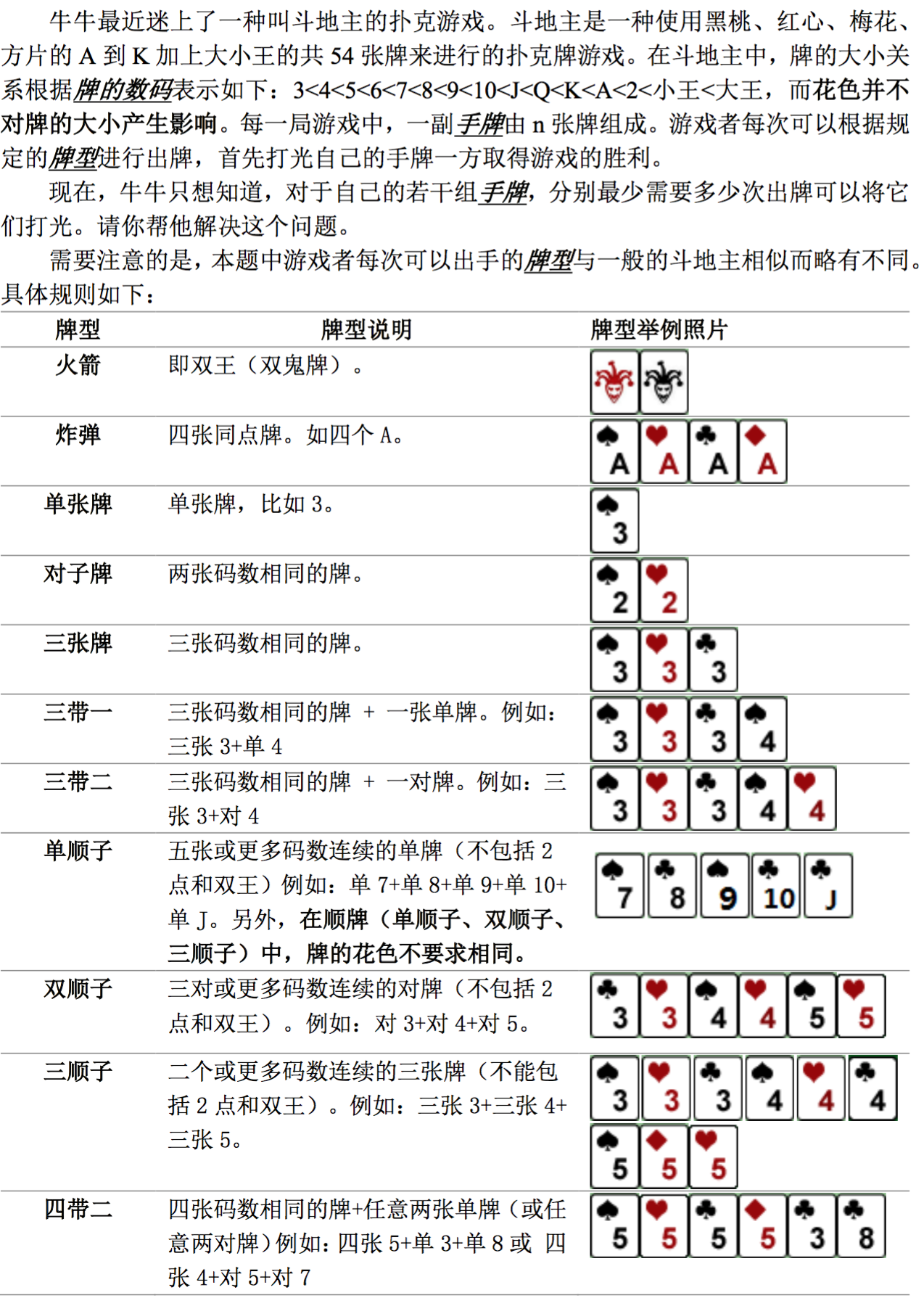
输入
第一行包含用空格隔开的2个正整数 T,n ,表示手牌的组数以及每组手牌的张数。
接下来 T 组数据,每组数据 n 行,每行一个非负整数对 ai,bi ,表示一张牌,其中 ai 表示牌的数码, bi 表示牌的花色,中间用空格隔开。特别的,我们用 1 来表示数码 A, 11 表示数码 J, 12 表示数码 Q, 13 表示数码 K;黑桃、红心、梅花、方片分别用 1-4 来表示;小王的表示方法为 0 1 ,大王的表示方法为 0 2 。
输出
共 T 行,每行一个整数,表示打光第
样例输入
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
样例输出

1 #include <cmath> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 #define ll long long 7 #define fo(i,x,y) for(int i=x; i<=y; i++) 8 #define pr(i,x,y) for(int i=x; i>=y; i--) 9 #define clear(a,x) memset(a,x,sizeof(a)) 10 #define INF 1e15 11 #define EPS 1e-8 12 13 using namespace std; 14 15 int t,N,x,y,a[5],b[14],MaxX; 16 17 inline ll read() 18 { 19 int f=1; 20 ll Tmp=0; 21 char ch=getchar(); 22 while (ch != '-' && ch < '0' || ch > '9') 23 { 24 ch=getchar(); 25 } 26 if (ch == '-') 27 { 28 f=-1; 29 ch=getchar(); 30 } 31 while (ch >= '0' && ch <= '9') 32 { 33 Tmp=Tmp * 10 + ch - 48; 34 ch=getchar(); 35 } 36 return Tmp * f; 37 } 38 39 40 int qiu() 41 { 42 int tot=0; 43 memset(a,0,sizeof(a)); 44 for(int i=0;i<=13;i++) 45 { 46 if (i) a[b[i]]++; 47 } 48 while(a[4] && a[2]>1) a[4]--,a[2]-=2,tot++; 49 while(a[4] && a[1]>1) a[4]--,a[1]-=2,tot++; 50 while(a[4] && a[2]) a[4]--,a[2]--,tot++; 51 while(a[3] && a[2]) a[3]--,a[2]--,tot++; 52 while(a[3] && a[1]) a[3]--,a[1]--,tot++; 53 return tot+a[1]+a[2]+a[3]+a[4]; 54 } 55 56 void dfs(int u) 57 { 58 if(u>=MaxX) return;int kk=qiu(); 59 if(u+kk<MaxX) MaxX=u+kk; 60 for(int i=2;i<=13;i++) 61 { 62 int j=i; 63 while(b[j]>=3 && j<=13) j++; 64 if(j-i>=2) 65 for(int v=i+1;v<=j-1;v++) 66 { 67 68 for(int vk=i;vk<=v;vk++) b[vk]-=3; 69 dfs(u+1); 70 for(int vk=i;vk<=v;vk++) b[vk]+=3; 71 } 72 } 73 for(int i=2;i<=13;i++) 74 { 75 int j=i; 76 while(b[j]>=2 && j<=13) j++; 77 if(j-i>=3) 78 for(int v=i+2;v<=j-1;v++) 79 { 80 for(int vk=i;vk<=v;vk++) b[vk]-=2; 81 dfs(u+1); 82 for(int vk=i;vk<=v;vk++) b[vk]+=2; 83 } 84 } 85 for(int i=2;i<=13;i++) 86 { 87 int j=i; 88 while(b[j]>=1 && j<=13) j++; 89 if(j-i>=5) 90 for(int v=i+4;v<=j-1;v++) 91 { 92 for(int vk=i;vk<=v;vk++) b[vk]--; 93 dfs(u+1); 94 for(int vk=i;vk<=v;vk++) b[vk]++; 95 } 96 } 97 } 98 99 int main() 100 { 101 int _=read(); 102 N=read(); 103 while (_--) 104 { 105 MaxX=2147483647; 106 clear(b,0); 107 fo(i,1,N) 108 { 109 int X,Y; 110 X=read(); Y=read(); 111 if (X == 1) 112 { 113 114 X=13; 115 } 116 else 117 { 118 if (X) 119 { 120 X--; 121 } 122 } 123 b[X]++; 124 } 125 dfs(0); 126 printf("%d\n",MaxX); 127 } 128 return 0; 129 }
Day2开始啦
T1:跳石头
题目描述
一年一度的“跳石头”比赛又要开始了! 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选
择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终 点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达 终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳 跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能 移走起点和终点的岩石)。
输入
输入文件第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终 点之间的岩石数,以及组委会至多移走的岩石数。
接下来 N 行,每行一个整数,第 i 行的整数 Di(0 < Di < L)表示第 i 块岩石与 起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同 一个位置。
输出
输出文件只包含一个整数,即最短跳跃距离的最大值。
样例输入
样例输出
提示
【输入输出样例 1 说明】
将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
【数据规模与约定】
对于 20%的数据,0 ≤ M ≤ N ≤ 10。对于50%的数据,0 ≤ M ≤ N ≤ 100。
对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
这道题目我们开始研究这个最终的答案是否具有二分性
如果X可行,那么X+1一定可行
如果X不可行,那么X-1一定不可行
所以我们就可以进行二分答案了

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 6 using namespace std; 7 8 int n,k; 9 int a[500005]; 10 11 bool check(int x) 12 { 13 int tmp=0;int h=0; 14 for (int i=1; i<=n; i++) 15 { 16 if (a[i]-h < x) 17 { 18 tmp++; 19 } 20 else h=a[i]; 21 } 22 if (tmp <= k) return true; 23 else return false; 24 } 25 26 int main() 27 { 28 a[0]=0; 29 int L; 30 scanf("%d%d%d",&L,&n,&k); 31 for (int i=1; i<=n; i++) 32 scanf("%d",&a[i]); 33 a[++n]=L; 34 int l=0,r=1000000000; 35 while (l<r) 36 { 37 //printf("%d %d\n",l,r); 38 int mid=(l+r+1)/2; 39 if (check(mid)) l=mid; 40 else r=mid-1; 41 } 42 printf("%d",l); 43 }
T2:子串
题目描述
有两个仅包含小写英文字母的字符串 A 和 B。现在要从字符串 A 中取出 k 个互不重叠的非空子串,然后把这 k 个子串按照其在字符串 A 中出现的顺序依次连接起来得到一 个新的字符串,请问有多少种方案可以使得这个新串与字符串 B 相等?注意:子串取出 的位置不同也认为是不同的方案。
输入
第一行是三个正整数 n,m,k,分别表示字符串 A 的长度,字符串 B 的长度,以及问题描述中所提到的 k,每两个整数之间用一个空格隔开。 第二行包含一个长度为 n 的字符串,表示字符串 A。 第三行包含一个长度为 m 的字符串,表示字符串 B。
输出
输出共一行,包含一个整数,表示所求方案数。由于答案可能很大,所以这里要求输出答案对 1,000,000,007 取模的结果。
样例输入
样例输出
那么就用一个数组s[i][j][kk]来表示在A串的前i个字符中选kk个子串匹配B串的前j个字符的方案数,A串的第i个字符会被取到.那么这个s数组该怎么推出来呢?可以发现,如果取第i个字符也有2种可能,因为kk是一定的,第i个字符可能和第i-1个字符合并成一个子串,那么从s[i-1][j][kk]转移过来,也可能不和第i-1个字符合并成一个子串,那么就要新开一个子串,故kk一定从kk-1转移过来,根据加法原理,那么s[i][j][kk] = s[i-1][j-1][kk] + f[i-1][j-1][kk-1].
还有一个问题:这是一个三维的状态转移方程!空间不一定开的下,再看数据范围,这绝对MLE,怎么办?注意到i只能从i或i-1转移过来,可以想到滚动数组
此处题解参考自某位大佬

1 #include <cmath> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 7 using namespace std; 8 9 int N,M,K; 10 int Mod1=1e9 + 7; 11 char s1[100005]; 12 char s2[100005]; 13 int dp[2][205][205]; 14 int S[2][205][205]; 15 16 int main() 17 { 18 scanf("%d%d%d",&N,&M,&K); 19 scanf("%s",s1+1); 20 scanf("%s",s2+1); 21 S[0][0][0]=1; 22 for (int i=1; i<=N; i++) 23 { 24 int Now=i & 1; 25 int Last=Now ^ 1; 26 S[Now][0][0]=1; 27 for (int j=1; j<=M; j++) 28 { 29 for (int k=1; k<=K; k++) 30 { 31 if (s1[i] == s2[j]) 32 { 33 dp[Now][j][k]=(dp[Last][j - 1][k] + S[Last][j - 1][k-1]) % Mod1; 34 } 35 else dp[Now][j][k]=0; 36 S[Now][j][k]=(S[Last][j][k] + dp[Now][j][k]) % Mod1; 37 } 38 } 39 } 40 printf("%d\n",S[N & 1][M][K]); 41 return 0; 42 }
T3:运输计划
题目描述
公元 2044 年,人类进入了宇宙纪元。
L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条
航道连通了 L 国的所有星球。
小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物
流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。
为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?
输入
接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第
输出
首先求出每个计划的路径长度 这里写的倍增 然后二分答案 对于每个ans 统计>他的路径条数 tot 并维护最大差值 dec 并且对于每条不合法的路径维护每个点的经过次数 然后枚举点 如果经过次数==tot说明每一条不合法的都经过他 然后尝试把它建成虫洞 如果他对应边的权值>=dec 那么我们删掉它ans就合法了 关键是统计每个点在非法路径中的经过次数 : 维护sum数组 对于每个非法的路径起点a b LCA(a,b)==s sum[a]++ sum[b]++ sum[s]-=2 这样网上更新的话 经过的点的sum值都变成1 祖先s的变成0 这样就实现了sum数组的维护
参考自某位大佬

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 6 using namespace std; 7 8 bool flag[1000005],flag1[1000005]; 9 int num,n,m; 10 int fa[300005][30]; 11 long long head[600005],sum[600005],dis[600005],L[600005],R[600005],p[600005],next[600005],father[600005],father1[600005],vet[600005],val[600005]; 12 long long dep[600005],dep1[600005]; 13 14 void add(int u,int v,int cost) 15 { 16 vet[++num]=v; 17 val[num]=cost; 18 next[num]=head[u]; 19 head[u]=num; 20 } 21 22 void dfs(int u) 23 { 24 flag1[u]=true; 25 int len=1; 26 while ((1 <<len) <= dep[u]) 27 { 28 fa[u][len]=fa[fa[u][len-1]][len-1]; 29 ++len; 30 } 31 int i=head[u]; 32 while (i != -1) 33 { 34 if (vet[i] != fa[u][0]) 35 { 36 dep[vet[i]]=dep[u]+1; 37 fa[vet[i]][0]=u; 38 father[vet[i]]=u; 39 father1[vet[i]]=val[i]; 40 dep1[vet[i]]=dep1[u]+val[i]; 41 dfs(vet[i]); 42 } 43 i=next[i]; 44 } 45 } 46 47 int lca(int x,int y) 48 { 49 if (dep[x] < dep[y]) 50 { 51 swap(x,y); 52 } 53 for (int i=20; i>=0; i--) 54 { 55 if (dep[x] - dep[y] >= (1 << i)) 56 { 57 x=fa[x][i]; 58 } 59 } 60 if (x == y) return x; 61 for (int i=20; i>=0; i--) 62 { 63 if (fa[x][i] != fa[y][i]) 64 { 65 x=fa[x][i]; 66 y=fa[y][i]; 67 } 68 } 69 return fa[x][0]; 70 } 71 72 void dfs1(int u) 73 { 74 flag[u]=true; 75 for (int i=head[u]; i!=-1; i=next[i]) 76 { 77 if (flag[vet[i]] == false) 78 { 79 dfs1(vet[i]); 80 sum[u]=sum[u]+sum[vet[i]]; 81 } 82 } 83 } 84 85 bool check(int x) 86 { 87 int ans=0; 88 for (int i=1; i<=n; i++) 89 { 90 sum[i]=0; 91 } 92 long long maxll=0; 93 for (int i=1; i<=m; i++) 94 { 95 if (dis[i] <= x) continue; 96 else 97 { 98 sum[L[i]]++; 99 sum[R[i]]++; 100 sum[p[i]]-=2; 101 ans++; 102 maxll=max(dis[i],maxll); 103 } 104 } 105 dfs1(1); 106 long long maxx=0; 107 for (int i=1; i<=n; i++) 108 { 109 if (sum[i] == ans) 110 { 111 maxx=max(maxx,father1[i]); 112 } 113 } 114 for (int i=1; i<=n; i++) 115 flag[i]=false; 116 for (int i=1; i<=n; i++) 117 { 118 sum[i]=0; 119 } 120 if (maxll - maxx <= x) return true; 121 else return false; 122 } 123 124 int find(int l,int r) 125 { 126 while (l < r) 127 { 128 int mid=(l + r) / 2; 129 //printf("%d\n",mid); 130 if (check(mid)) r=mid; 131 else l=mid+1; 132 } 133 return l; 134 } 135 136 int main() 137 { 138 num=0; 139 scanf("%d%d",&n,&m); 140 for (int i=1; i<=n; i++) 141 head[i]=-1; 142 for (int i=1; i<n; i++) 143 { 144 int u,v,cost; 145 scanf("%d%d%d",&u,&v,&cost); 146 add(u,v,cost); 147 add(v,u,cost); 148 } 149 memset(flag1,false,sizeof(flag1)); 150 dep1[1]=0; 151 dfs(1); 152 int max1=0; 153 for (int i=1; i<=m; i++) 154 { 155 scanf("%d%d",&L[i],&R[i]); 156 p[i]=lca(L[i],R[i]); 157 dis[i]=dep1[L[i]]+dep1[R[i]]-2*dep1[p[i]]; 158 max1=max(max1,(int) dis[i]); 159 } 160 //for (int i=1; i<=m; i++) 161 // printf("%d\n",dis[i]); 162 int XXX=find(0,max1); 163 printf("%d\n",XXX); 164 }
最后我想说两句话
Hala Madrid!
李沁么么哒


