基于马尔科夫链的产品评估预测
马尔可夫链
1、建立转移概率矩阵:
马尔可夫链是一种时间离散、状态离散、带有记忆功能情况的随机过程，是预测中常用到的一种数学模型。如果数据的本身的每一时刻的状态仅仅取决于紧接在他前面的随机变量的所处状态，而与这之前的状态无关，这就是马尔可夫链的“无后效性”。
经过了解本文的销量对于时间序列敏感性不高，具有“无后效性”的特点，因此可以根据唯品历史以来的销量进行其预测，可以得到下一次档期每个商品的销售状态。
为了准确的计算整个目标系统的转移概率矩阵是马尔可夫链预测方法最常用到也是最基础的内容，一般是经常是使用统计估算法，将其方法总结如下：
假设我们所关注的序列片段存在状态的个数为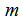
个，即状态空间
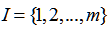，将
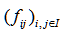看作为转移频数生成的概率矩阵。第
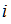行，第
行元素在这个转移频数矩阵的值
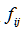除以全部元素和得到的值定义为“转移概率”，用字母
，
来表示，既有：
由状态
经一步转到状态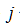
也可以用此公式来表示。因为稳定性好是频率的一个特点，所以如果
很大的时候，我们可以把频率等价的看成是概率，因而可以用它来估算转移概率。实际写法上为了方便转移频率用符号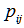
来表示，并称之为“转移概率”，一步转移概率也相应的表示为：
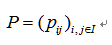
2、对离散型数列进行“马氏性”检验:
通常情况下选用离散型序列的马尔可夫链来对变量具有随机性的序列进行“马氏性”检验，检验常用
统计量。
设研究的序列状态个数为
，用
表示转移频数概率矩阵，把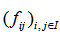
的各个列之和去除以
的全部元素之和，就会得到“边际概率”，用字母
表示，其中：
当
很大时
统计量：
它将服从自由度为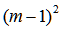
的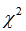
分布，现在给定显著性水平为
，经查表可得到的值
（或者在excel表里面利用公式chiinv(
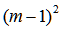, )计算得到）。如果
，则拒绝零假设，可以认为序列具备“马氏性”，反之，则这个序列不能当作马尔可夫链来对待。
假设某一款商品的销量是如下所示：
|
825058101 |
66 |
39 |
50 |
45 |
96 |
38 |
15 |
14 |
22 |
63 |
|
22 |
63 |
80 |
42 |
43 |
104 |
45 |
20 |
7 |
3 |
本文设定不同的销售量有不同的状态，即：
|
范围 |
状态 |
|
<20 |
滞销 |
|
20<=and<40 |
平销 |
|
40<=and<60 |
热销 |
|
>60 |
畅销 |
由此可以得到上述商品的转移过程的：
|
滞销 |
平销 |
热销 |
畅销 |
|
|
滞销 |
2 |
1 |
0 |
0 |
|
平销 |
2 |
0 |
1 |
1 |
|
热销 |
0 |
1 |
2 |
2 |
|
畅销 |
0 |
2 |
2 |
1 |
则该商品的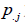
为：
|
滞销 |
平销 |
热销 |
畅销 |
|
4/18 |
4/18 |
5/18 |
5/18 |
则该商品的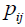
为：
|
滞销 |
平销 |
热销 |
畅销 |
|
|
滞销 |
0.67 |
0.33 |
0.00 |
0.00 |
|
平销 |
0.50 |
0.00 |
0.25 |
0.25 |
|
热销 |
0.00 |
0.20 |
0.40 |
0.40 |
|
畅销 |
0.00 |
0.40 |
0.40 |
0.20 |
将上述结果代入公式：
根据卡方分布的数据比较大小：
该商品的卡方值为：大于0.1显著水平下的
，所以该商品是通过“马氏性”检验的，因此该商品的转移概率矩阵为：
|
|
滞销 |
平销 |
热销 |
畅销 |
|
滞销 |
0.6139 |
0.2211 |
0.0825 |
0.0825 |
|
平销 |
0.335 |
0.315 |
0.2 |
0.15 |
|
热销 |
0.1 |
0.24 |
0.37 |
0.29 |
|
畅销 |
0.2 |
0.16 |
0.34 |
0.3 |
该表格表示为：
(1)原来产品为滞销状态，下一次则有61.39%的概率还是滞销状态，有22.11%的概率变为平销，有8.25%的概率变为热销，有8.25%的概率变为畅销；
(2) 原来产品为平销状态，下一次则有33.50%的概率还是滞销状态，有31.50%的概率变为平销，有20.00%的概率变为热销，有15.00%的概率变为畅销；
(3) 原来产品为热销状态，下一次则有10.00%的概率还是滞销状态，有24.00%的概率变为平销，有37.00%的概率变为热销，有29.00%的概率变为畅销；
(4) 原来产品为热销状态，下一次则有20.00%的概率还是滞销状态，有16.00%的概率变为平销，有34.00%的概率变为热销，有30.00%的概率变为畅销。
-----------------------------------我是分割线-------------------------------
但是但是，这只是其中一个商品的预估
本店商品的其中一个
本店差不多有1700商品
怎么办怎么办？
首先将数据储存出来
本文用python读取数据
步骤1：excel表格的数据插入进去啊，这里是读取表格
from openpyxl import load_workbook
1 if __name__ == '__main__': 2 3 ##这里是打开excel将数据储存到数组里面 4 wb = load_workbook(filename=r'C:\Users\Administrator\Desktop\data.xlsx') ##读取路径 5 ws = wb.get_sheet_by_name("Sheet1") ##读取名字为Sheet1的sheet表 6 info_data_id = [] 7 info_data_sales = []
步骤2：表格读取：
1 2 for row_A in range(2, 1693): ## 遍历第2行到1692行 3 id = ws.cell(row=row_A, column=1).value ## 遍历第2行到1692行，第1列 4 info_data_id.append(id) 5 for row_num_BtoU in range(2, len(info_data_id) + 2): ## 遍历第2行到1692行 6 row_empty = [] ##建立一个空数组作为临时储存地，每次换行就被清空 7 for i in range(2, 22): ## 遍历第2行到1692行，第2到21列 8 data = ws.cell(row=row_num_BtoU, column=i).value 9 if data == None: 10 pass 11 else: 12 row_empty.append(data) ##将单元格信息储存进去 13 info_data_sales.append(row_empty) ##row_empty每次储存完2到21列后压给info_data_sales，然后row_empty被清空
重点是建立了一个空的row_empty = []可以临时储存每一行的数据，等到下一次循环就被清空
表格数据样式如下：
一共1692行22列应该，反正没数
步骤3：计算p.j
1 ##这里是计算pj的 2 info_pj = [] 3 for j in range(0, len(info_data_sales)): 4 pj_zhixiao = 0 5 pj_pingxiao = 0 6 pj_rexiao = 0 7 number = 0 8 pj_empty = [] 9 for k in range(0, len(info_data_sales[j])): 10 number = number + 1 11 if info_data_sales[j][k] < 10: 12 pj_zhixiao = pj_zhixiao + 1 13 elif info_data_sales[j][k] >= 10 and info_data_sales[j][k] < 30: 14 pj_pingxiao = pj_pingxiao + 1 15 elif info_data_sales[j][k] >= 30: 16 pj_rexiao = pj_rexiao + 1 17 chance_zhixiao = pj_zhixiao / number 18 chance_pingxiao = pj_pingxiao / number 19 chance_rexiao = pj_rexiao / number 20 pj_empty.append(chance_zhixiao) 21 pj_empty.append(chance_pingxiao) 22 pj_empty.append(chance_rexiao) 23 info_pj.append(pj_empty) ##得到了pj初始概率
遍历数组info_data_sales的每一个元素，根据我审定的判断来计算各个状态的出现概率：
|
范围 |
状态 |
|
<10 |
滞销 |
|
10<=and<30 |
平销 |
|
>30 |
热销 |
步骤4：计算pij和fij：
1 ##这里是计算fij和pij的 2 info_fij = [] 3 info_pij = [] 4 for j in range(0, len(info_data_sales)): 5 fij_zz = 0 6 fij_zp = 0 7 fij_zr = 0 8 fij_pz = 0 9 fij_pp = 0 10 fij_pr = 0 11 fij_rz = 0 12 fij_rp = 0 13 fij_rr = 0 14 fij_first = [] 15 fij_second = [] 16 fij_third = [] 17 fij_empty = [] 18 pij_first = [] 19 pij_second = [] 20 pij_third = [] 21 pij_empty = [] 22 23 for k in range(0, len(info_data_sales[j])): 24 if k + 1 > len(info_data_sales[j]) - 1: 25 pass 26 else: 27 if info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] < 10: 28 fij_zz = fij_zz + 1 29 elif info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 30 fij_zp = fij_zp + 1 31 elif info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] >= 30: 32 fij_zr = fij_zr + 1 33 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] < 10: 34 fij_pz = fij_pz + 1 35 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 36 fij_pp = fij_pp + 1 37 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] >= 30: 38 fij_pr = fij_pr + 1 39 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] < 10: 40 fij_rz = fij_rz + 1 41 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 42 fij_rp = fij_rp + 1 43 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] >= 30: 44 fij_rr = fij_rr + 1 45 46 ##这里计算fij 47 if fij_zz + fij_zp + fij_zr == 0: 48 fij_zz = 1 49 if fij_pz + fij_pp + fij_pr == 0: 50 fij_pp = 1 51 if fij_rz + fij_rp + fij_rr == 0: 52 fij_rr = 1 53 fij_first.append(fij_zz) 54 fij_first.append(fij_zp) 55 fij_first.append(fij_zr) 56 fij_second.append(fij_pz) 57 fij_second.append(fij_pp) 58 fij_second.append(fij_pr) 59 fij_third.append(fij_rz) 60 fij_third.append(fij_rp) 61 fij_third.append(fij_rr) 62 fij_empty.append(fij_first) 63 fij_empty.append(fij_second) 64 fij_empty.append(fij_third) 65 info_fij.append(fij_empty) 66 # print(info_fij) 67 68 ##这里计算pij 69 pij_first.append(fij_zz / (fij_zz + fij_zp + fij_zr)) 70 pij_first.append(fij_zp / (fij_zz + fij_zp + fij_zr)) 71 pij_first.append(fij_zr / (fij_zz + fij_zp + fij_zr)) 72 pij_second.append(fij_pz / (fij_pz + fij_pp + fij_pr)) 73 pij_second.append(fij_pp / (fij_pz + fij_pp + fij_pr)) 74 pij_second.append(fij_pr / (fij_pz + fij_pp + fij_pr)) 75 pij_third.append(fij_rz / (fij_rz + fij_rp + fij_rr)) 76 pij_third.append(fij_rp / (fij_rz + fij_rp + fij_rr)) 77 pij_third.append(fij_rr / (fij_rz + fij_rp + fij_rr)) 78 79 pij_empty.append(pij_first) 80 pij_empty.append(pij_second) 81 pij_empty.append(pij_third) 82 info_pij.append(pij_empty)
先是统计各个状态出现的概率
再压入数组里面
步骤5：判断马氏性
什么数据又有了，那么就可以用公式计算了：
代码如下：
1 ##马氏性判断 2 info_judge = [] 3 for m in range(0, len(info_pij)): 4 sum = 0 5 for n in range(0, len(info_pij[m])): 6 sum_1 = 0 7 sum_2 = 0 8 sum_3 = 0 9 if info_fij[m][n][0] == 0 or info_pij[m][n][0] == 0 or info_pj[m][0] == 0: 10 sum_1 = 0 11 else: 12 sum_1 = info_fij[m][n][0] * abs(math.log(info_pij[m][n][0] / info_pj[m][0], math.e)) 13 if info_fij[m][n][1] == 0 or info_pij[m][n][1] == 0 or info_pj[m][1] == 0: 14 sum_2 = 0 15 else: 16 sum_2 = info_fij[m][n][1] * abs(math.log(info_pij[m][n][1] / info_pj[m][1], math.e)) 17 if info_fij[m][n][2] == 0 or info_pij[m][n][2] == 0 or info_pj[m][2] == 0: 18 sum_3 = 0 19 else: 20 sum_3 = info_fij[m][n][2] * abs(math.log(info_pij[m][n][2] / info_pj[m][2], math.e)) 21 22 sum = sum + 2 * (sum_1 + sum_2 + sum_3) 23 info_judge.append(sum)
不要忘记了
import math
由于我的显著性非常不明显
所以用了0.2的显著性判断：
1 info_result = [] 2 for a in info_judge: 3 if a > 5.988617: 4 info_result.append("具有马氏性") 5 else: 6 info_result.append("无")
步骤6：压回excel表格就行了
这里用到的是
import xlsxwriter
1 first = ['是否具有马氏性'] 2 workbook = xlsxwriter.Workbook('C:\\Users\\Administrator\\Desktop\\data1.xlsx') 3 worksheet = workbook.add_worksheet() # 创建一个工作表对象 4 font = workbook.add_format( 5 {'border': 1, 'align': 'center', 'font_size': 11, 'font_name': '微软雅黑'}) ##字体居中，11号，微软雅黑,给一般的信息用的 6 worksheet.write(0, 1, '是否具有马氏性') 7 worksheet.write(0, 0, '货号', font) 8 worksheet.write(0, 2, '原状态是', font) 9 worksheet.write(0, 3, '滞销', font) 10 worksheet.write(0, 4, '平销', font) 11 worksheet.write(0, 5, '热销', font)
步骤7：记得利用矩阵计算啊，python自带的矩阵运算是：
import numpy as np
1 for x in range(0, len(info_result)): 2 worksheet.write(x + 1, 1, info_result[x], font) ##写入马氏性判断结果 3 worksheet.write(x + 1, 0, info_data_id[x], font) ##写入商品货号 4 matrix_a = info_pij[x] ##单独拿出第一个数组 5 matrix_c = np.array(matrix_a) ##将数组转化为矩阵 6 matrix = matrix_c * matrix_c ##矩阵相乘 7 row = 3 8 if info_data_sales[x][len(info_data_sales[x]) - 1] < 10: 9 worksheet.write(x + 1, 2, "滞销", font) 10 for y in matrix[0]: 11 worksheet.write(x + 1, row, y, font) 12 row = row + 1 13 if info_data_sales[x][len(info_data_sales[x]) - 1] >= 10 and info_data_sales[x][ 14 len(info_data_sales[x]) - 1] < 30: 15 worksheet.write(x + 1, 2, "平销", font) 16 for y in matrix[1]: 17 worksheet.write(x + 1, row, y, font) 18 row = row + 1 19 if info_data_sales[x][len(info_data_sales[x]) - 1] >= 30: 20 worksheet.write(x + 1, 2, "热销", font) 21 for y in matrix[2]: 22 worksheet.write(x + 1, row, y, font) 23 row = row + 1 24 workbook.close()
最后做个好学生，不要忘记关掉excel表格
workbook.close()
得到效果图如下啊啊啊啊：
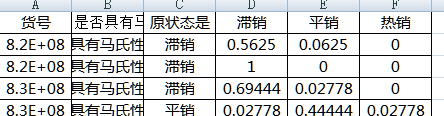
最后附上全部代码：
python
Markov.py
1 # -*- coding:utf-8 -*- 2 from openpyxl import Workbook 3 from openpyxl import load_workbook 4 import math 5 import xlsxwriter 6 import numpy as np 7 8 if __name__ == '__main__': 9 10 ##这里是打开excel将数据储存到数组里面 11 wb = load_workbook(filename=r'C:\Users\Administrator\Desktop\data.xlsx') ##读取路径 12 ws = wb.get_sheet_by_name("Sheet1") ##读取名字为Sheet1的sheet表 13 info_data_id = [] 14 info_data_sales = [] 15 16 a = 0 17 for row_A in range(2, 1693): ## 遍历第2行到1692行 18 id = ws.cell(row=row_A, column=1).value ## 遍历第2行到1692行，第1列 19 info_data_id.append(id) 20 for row_num_BtoU in range(2, len(info_data_id) + 2): ## 遍历第2行到1692行 21 row_empty = [] ##建立一个空数组作为临时储存地，每次换行就被清空 22 for i in range(2, 22): ## 遍历第2行到1692行，第2到21列 23 data = ws.cell(row=row_num_BtoU, column=i).value 24 if data == None: 25 pass 26 else: 27 row_empty.append(data) ##将单元格信息储存进去 28 info_data_sales.append(row_empty) ##row_empty每次储存完2到21列后压给info_data_sales，然后row_empty被清空 29 30 ##这里是计算pj的 31 info_pj = [] 32 for j in range(0, len(info_data_sales)): 33 pj_zhixiao = 0 34 pj_pingxiao = 0 35 pj_rexiao = 0 36 number = 0 37 pj_empty = [] 38 for k in range(0, len(info_data_sales[j])): 39 number = number + 1 40 if info_data_sales[j][k] < 10: 41 pj_zhixiao = pj_zhixiao + 1 42 elif info_data_sales[j][k] >= 10 and info_data_sales[j][k] < 30: 43 pj_pingxiao = pj_pingxiao + 1 44 elif info_data_sales[j][k] >= 30: 45 pj_rexiao = pj_rexiao + 1 46 chance_zhixiao = pj_zhixiao / number 47 chance_pingxiao = pj_pingxiao / number 48 chance_rexiao = pj_rexiao / number 49 pj_empty.append(chance_zhixiao) 50 pj_empty.append(chance_pingxiao) 51 pj_empty.append(chance_rexiao) 52 info_pj.append(pj_empty) ##得到了pj初始概率 53 ##这里是计算fij和pij的 54 info_fij = [] 55 info_pij = [] 56 for j in range(0, len(info_data_sales)): 57 fij_zz = 0 58 fij_zp = 0 59 fij_zr = 0 60 fij_pz = 0 61 fij_pp = 0 62 fij_pr = 0 63 fij_rz = 0 64 fij_rp = 0 65 fij_rr = 0 66 fij_first = [] 67 fij_second = [] 68 fij_third = [] 69 fij_empty = [] 70 pij_first = [] 71 pij_second = [] 72 pij_third = [] 73 pij_empty = [] 74 75 for k in range(0, len(info_data_sales[j])): 76 if k + 1 > len(info_data_sales[j]) - 1: 77 pass 78 else: 79 if info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] < 10: 80 fij_zz = fij_zz + 1 81 elif info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 82 fij_zp = fij_zp + 1 83 elif info_data_sales[j][k] < 10 and info_data_sales[j][k + 1] >= 30: 84 fij_zr = fij_zr + 1 85 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] < 10: 86 fij_pz = fij_pz + 1 87 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 88 fij_pp = fij_pp + 1 89 elif info_data_sales[j][k] < 30 and info_data_sales[j][k + 1] >= 30: 90 fij_pr = fij_pr + 1 91 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] < 10: 92 fij_rz = fij_rz + 1 93 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] < 30 and info_data_sales[j][k + 1] >= 10: 94 fij_rp = fij_rp + 1 95 elif info_data_sales[j][k] >= 30 and info_data_sales[j][k + 1] >= 30: 96 fij_rr = fij_rr + 1 97 98 ##这里计算fij 99 if fij_zz + fij_zp + fij_zr == 0: 100 fij_zz = 1 101 if fij_pz + fij_pp + fij_pr == 0: 102 fij_pp = 1 103 if fij_rz + fij_rp + fij_rr == 0: 104 fij_rr = 1 105 fij_first.append(fij_zz) 106 fij_first.append(fij_zp) 107 fij_first.append(fij_zr) 108 fij_second.append(fij_pz) 109 fij_second.append(fij_pp) 110 fij_second.append(fij_pr) 111 fij_third.append(fij_rz) 112 fij_third.append(fij_rp) 113 fij_third.append(fij_rr) 114 fij_empty.append(fij_first) 115 fij_empty.append(fij_second) 116 fij_empty.append(fij_third) 117 info_fij.append(fij_empty) 118 # print(info_fij) 119 120 ##这里计算pij 121 pij_first.append(fij_zz / (fij_zz + fij_zp + fij_zr)) 122 pij_first.append(fij_zp / (fij_zz + fij_zp + fij_zr)) 123 pij_first.append(fij_zr / (fij_zz + fij_zp + fij_zr)) 124 pij_second.append(fij_pz / (fij_pz + fij_pp + fij_pr)) 125 pij_second.append(fij_pp / (fij_pz + fij_pp + fij_pr)) 126 pij_second.append(fij_pr / (fij_pz + fij_pp + fij_pr)) 127 pij_third.append(fij_rz / (fij_rz + fij_rp + fij_rr)) 128 pij_third.append(fij_rp / (fij_rz + fij_rp + fij_rr)) 129 pij_third.append(fij_rr / (fij_rz + fij_rp + fij_rr)) 130 131 pij_empty.append(pij_first) 132 pij_empty.append(pij_second) 133 pij_empty.append(pij_third) 134 info_pij.append(pij_empty) 135 # print(len(info_pij)) 136 137 ##马氏性判断 138 info_judge = [] 139 for m in range(0, len(info_pij)): 140 sum = 0 141 for n in range(0, len(info_pij[m])): 142 sum_1 = 0 143 sum_2 = 0 144 sum_3 = 0 145 if info_fij[m][n][0] == 0 or info_pij[m][n][0] == 0 or info_pj[m][0] == 0: 146 sum_1 = 0 147 else: 148 sum_1 = info_fij[m][n][0] * abs(math.log(info_pij[m][n][0] / info_pj[m][0], math.e)) 149 if info_fij[m][n][1] == 0 or info_pij[m][n][1] == 0 or info_pj[m][1] == 0: 150 sum_2 = 0 151 else: 152 sum_2 = info_fij[m][n][1] * abs(math.log(info_pij[m][n][1] / info_pj[m][1], math.e)) 153 if info_fij[m][n][2] == 0 or info_pij[m][n][2] == 0 or info_pj[m][2] == 0: 154 sum_3 = 0 155 else: 156 sum_3 = info_fij[m][n][2] * abs(math.log(info_pij[m][n][2] / info_pj[m][2], math.e)) 157 158 sum = sum + 2 * (sum_1 + sum_2 + sum_3) 159 info_judge.append(sum) 160 # print(len(info_pij)) 161 # print(len(info_pj)) 162 # print(len(info_fij)) 163 # print(info_judge) 164 # print(len(info_judge)) 165 info_result = [] 166 for a in info_judge: 167 if a > 5.988617: 168 info_result.append("具有马氏性") 169 else: 170 info_result.append("无") 171 # print(info_result) 172 # print(info_pij[0]) 173 174 ##下面是计算一阶马尔可夫链预测，即矩阵的运算的方法 175 # matrix_a = info_pij[0] 176 # matrix_c = np.array(matrix_a) 177 # matrix = matrix_c * matrix_c 178 # print(matrix) 179 # print(matrix_c) 180 # print(len(info_pij)) 181 # print(len(info_data_sales)) 182 # print(info_data_sales[0]) 183 # if info_data_sales[0][len(info_data_sales[0]) - 1] < 10: 184 # print(info_data_sales[0][len(info_data_sales[0]) - 1]) 185 # print('滞销') 186 # print(matrix[1]) 187 188 ##下面是写入excel表格 189 first = ['是否具有马氏性'] 190 workbook = xlsxwriter.Workbook('C:\\Users\\Administrator\\Desktop\\data1.xlsx') 191 worksheet = workbook.add_worksheet() # 创建一个工作表对象 192 font = workbook.add_format( 193 {'border': 1, 'align': 'center', 'font_size': 11, 'font_name': '微软雅黑'}) ##字体居中，11号，微软雅黑,给一般的信息用的 194 worksheet.write(0, 1, '是否具有马氏性') 195 worksheet.write(0, 0, '货号', font) 196 worksheet.write(0, 2, '原状态是', font) 197 worksheet.write(0, 3, '滞销', font) 198 worksheet.write(0, 4, '平销', font) 199 worksheet.write(0, 5, '热销', font) 200 for x in range(0, len(info_result)): 201 worksheet.write(x + 1, 1, info_result[x], font) ##写入马氏性判断结果 202 worksheet.write(x + 1, 0, info_data_id[x], font) ##写入商品货号 203 matrix_a = info_pij[x] ##单独拿出第一个数组 204 matrix_c = np.array(matrix_a) ##将数组转化为矩阵 205 matrix = matrix_c * matrix_c ##矩阵相乘 206 row = 3 207 if info_data_sales[x][len(info_data_sales[x]) - 1] < 10: 208 worksheet.write(x + 1, 2, "滞销", font) 209 for y in matrix[0]: 210 worksheet.write(x + 1, row, y, font) 211 row = row + 1 212 if info_data_sales[x][len(info_data_sales[x]) - 1] >= 10 and info_data_sales[x][ 213 len(info_data_sales[x]) - 1] < 30: 214 worksheet.write(x + 1, 2, "平销", font) 215 for y in matrix[1]: 216 worksheet.write(x + 1, row, y, font) 217 row = row + 1 218 if info_data_sales[x][len(info_data_sales[x]) - 1] >= 30: 219 worksheet.write(x + 1, 2, "热销", font) 220 for y in matrix[2]: 221 worksheet.write(x + 1, row, y, font) 222 row = row + 1 223 workbook.close()
