【机器学习】算法原理详细推导与实现(二):逻辑回归

【机器学习】算法原理详细推导与实现(二):逻辑回归

在上一篇算法中，线性回归实际上是 连续型 的结果，即 \(y\in R\) ，而逻辑回归的 \(y\) 是离散型，只能取两个值 \(y\in \{0,1\}\)，这可以用来处理一些分类的问题。

logistic函数

我们可能会遇到一些分类问题，例如想要划分 鸢尾花 的种类，尝试基于一些特征来判断鸢尾花的品种，或者判断上一篇文章中的房子，在6个月之后能否被卖掉，答案是 是 或者 否，或者一封邮件是否是垃圾邮件。所以这里是 \(x\) ，这里是 \(y\) 在一个分类问题中，\(y\) 只能取两个值0和1，这就是一个二元分类的问题，如下所示：

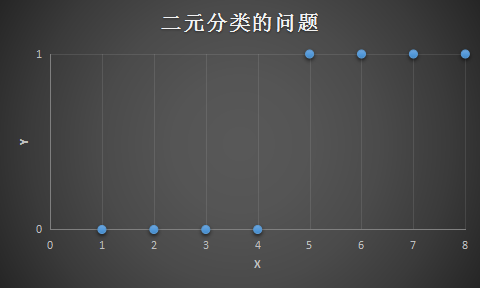
可以使用线性回归对以上数值进行划分，可以拟合出如下那么一条线，用 \(y=0.5\) 作为临界点，如果 \(x\) 在这个临界点的右侧，那么 \(y\) 的值就是1，如果在临界点的左侧，那么 \(y\) 的值就是0，所以确实会有一些人会这么做，用线性回归解决分类问题：

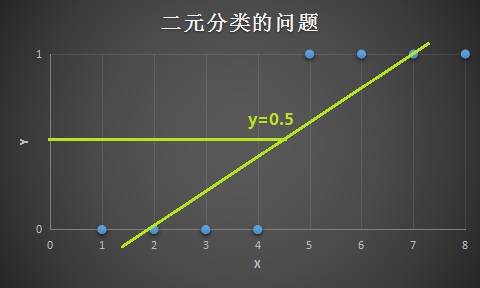
线性回归解决分类问题，有时候它的效果很好，但是通常用线性回归解决像这样的分类问题会是一个很糟糕的主意，加入存在一个额外的训练样本 \(x=12\)，如果现在对这个训练集合做线性拟合，那么可能拟合出来那么一条直线：

这时候\(y\)的临界点估计已经不太合适了，可以知道线性回归对于分类问题来说，不是一个很好的方法。

假设 \(h_\theta(x) \in [0,1]\)，当如果已知 \(y\in \{0,1\}\)，那么至少应该让假设 \(h_\theta(x)\) 预测出来的值不会比1大太多，也不会比0小太多，所以一般不会选择线性函数作为假设，而是会选择一些稍微不同的函数图像：

\[g(z)=\frac{1}{1+e^{-z}} \]

\[h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \]

\(g(z)\) 被称为 sigmoid函数 ，也通常被称为 logistic函数，它的函数图像是：

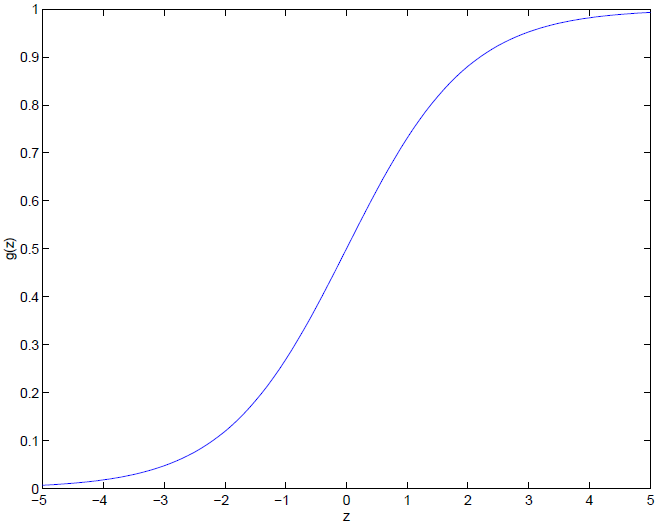
当 \(z\) 变得非常小的时候，\(g(x)\) 会趋向于0，当\(z\)变得非常大的时候，\(g(x)\) 会趋向于1，它和纵轴相较于0.5。

逻辑回归

那么我们的假设\(h_\theta(x)\) 要尝试估计 \(y\in \{0,1\}\) 的概率，即：

\[P(y=1|x;\theta)=h_\theta(x) \]

\[P(y=0|x;\theta)=1-h_\theta(x) \]

以上可以把两个公式合并简写为（如果\(y=1\)那么公式为\(h_\theta(x)\)；如果\(y=0\)那么公式为\(1-h_\theta(x)\)）：

\[P(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} \]

如果对《概率论和数理统计》学得好的人不难看出，以上函数其实就是 伯努利分布 的函数。

对于每一个假设值\(h_\theta(x)\)，为了使每一次假设值更准确，即当 \(y=1\) 时估计函数 \(P(y=1|x;\theta)=h_\theta(x)\) 趋向于1，当\(y=0\) 时估计函数 \(P(y=0|x;\theta)=1-h_\theta(x)\) 趋向于0。则对于每一个\((x_i,y_i)\)，参数 \(\theta\) 的似然估计 \(L(\theta)\)为：

\[\begin{split} L(\theta)&=P(\vec{y}|X;\theta) \\ &=\prod_{i=1}^mP(y^{(i)}|x^{(i)};\theta) \\ &=\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-{y^{(i)}}} \end{split} \]

如果每一个\((x_i,y_i)\)都准确，即 \(P(y|x;\theta)\) 趋向于1，则应该使似然估计 \(L(\theta)\) 最大化，也就是转化成熟悉的问题：求解 \(L(\theta)\) 的极大似然估计。

为了调整参数 \(\theta\) 使似然估计 \(L(\theta)\) 最大化，推导如下（取 \(log\) 是为了去掉叠乘方便计算）：

\[\begin{split} l(\theta)&=logL(\theta) \\ &=\sum_{i=1}^m{y^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)}))} \end{split} \]

为了使这个函数最大，同样可以使用前面学习过的梯度上升算法使对数似然估计最大化。之前学习的是要使误差和 最小化，所以梯度下降的公式为：

\[\theta:=\theta-\alpha\frac{\partial J(\theta)}{\partial\theta}=>\theta:=\theta-\alpha\nabla_\theta J(\theta) \]

而本次为了求解似然估计最大化，使用的是梯度上升：

\[\theta:=\theta+\alpha\nabla_\theta l(\theta)=>\theta:=\theta+\alpha\frac{\partial l(\theta)}{\partial\theta} \]

对数似然性是和 \(\theta\) 有关，同样的为了计算 梯度上升 最快的方向，要对上述公式求偏导得到极值，即是上升最快的方向：

\[\begin{split} \frac{\partial l(\theta)}{\partial\theta_j}&=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})\frac{\partial}{\partial\theta_j}g(\theta^Tx) \\ &=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})g(\theta^Tx)(1-g(\theta^Tx))\frac{\partial}{\partial\theta_j}\theta^Tx \\ &=(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx))x_j \\ &=(y-g(\theta^Tx))x_j \\ &=(y-h_{\theta}(x))x_j \end{split} \]

则对于 m 个样本，则有：

\[\frac{\partial l(\theta)}{\partial\theta_j}=\sum_{i=1}^m{(y-h_{\theta}(x))x_j} \]

\[\theta_j:=\theta_j+\sum_{i=1}^m{(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j} \]

所以总结来说：

逻辑回归假设数据服从伯努利分布，通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

逻辑回归是分类为什么叫做回归

简单来回答，其实logistic regression是一种广义线性模型\(z=\theta x+b\)，但是这个得到的输出不在范围[0,1]（为什么需要是[0,1]，因为如果做二分类的话，label是服从伯努利分布的，训练时给定的label非0即1），为了使其输出的结果在范围[0,1]所以增加了sigmoid激活函数，对输出值进行再次激活。

从公式推理来说，原始的回归函数是：

\[z=\theta x+b \]

其中\(z \in R\)

为了使其线性函数达到分类的效果，对其结果\(z\)进行类似一种“归一化”的操作，即增加激活函数sigmoid：

\[y=\frac{1}{1+e^{-(\theta x+b)}} \]

上面这个函数倒推回来就可以变化成：

\[\ln\frac{y}{1-y}=z=\theta x+b \]

\(y\)看作样本\(x\)为正例的可能性，相应的\(1-y\)就是样本\(x\)为反例的可能性，两者的比值\(\frac{y}{1-y}\)叫做几率（odds），取对数\(\ln\frac{y}{1-y}\)后叫做对数几率（logistic odds），对数几率与\(x\)是线性关系，所以可以称作“回归”。

鸢尾花分类

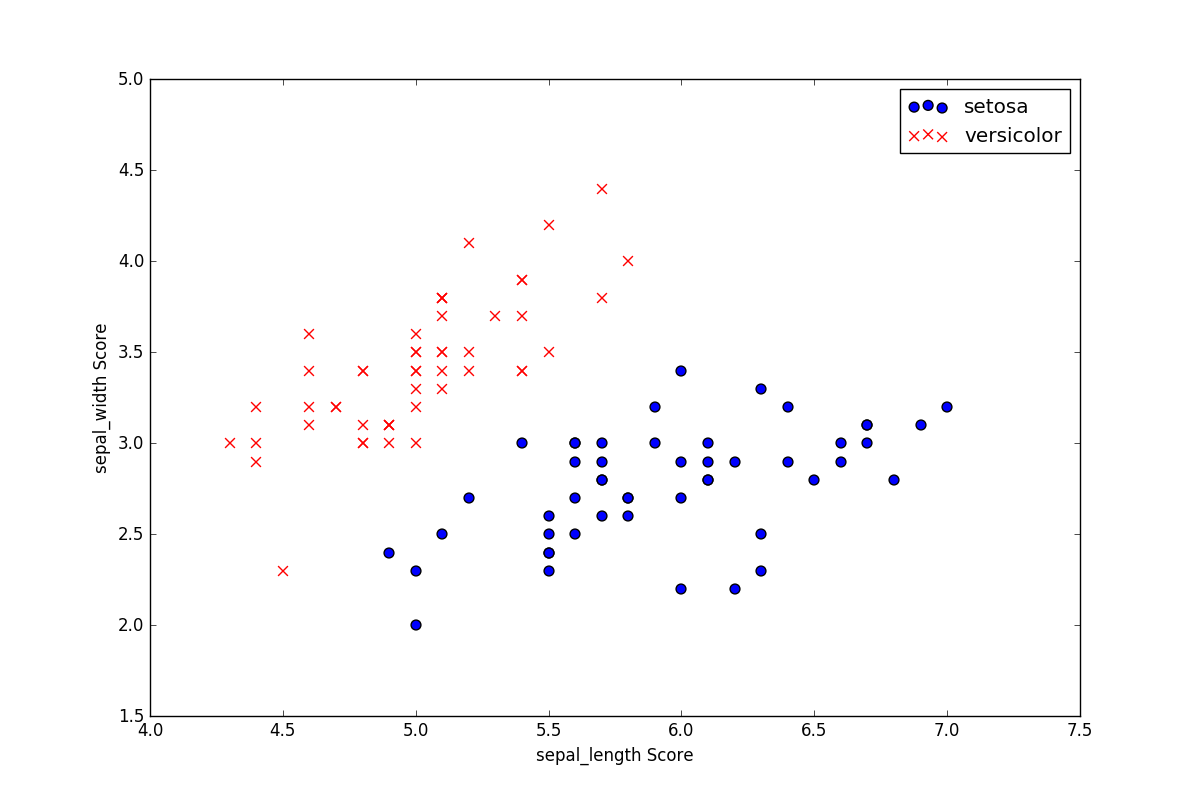
为了划分 鸢尾花 的种类，尝试基于一些特征来判断鸢尾花的品种，选取100条鸢尾花数据集如下所示：

花萼长度（单位cm）	花萼宽度（单位cm）	种类
5.1	3.5	0
4.9	3.0	0
4.7	3.2	0
7.0	3.2	1
6.4	3.2	1
...	...	...

其中：

种类	含义
0	山鸢尾（setosa）
1	变色鸢尾（versicolor）
2	维吉尼亚鸢尾（virginica）

数据集的图像分布为：

计算损失函数：

# 损失函数
def computeCost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))

梯度下降函数为：

# 梯度下降
def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)

    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)

    error = sigmoid(X * theta.T) - y

    for i in range(parameters):
        term = np.multiply(error, X[:, i])
        grad[i] = np.sum(term) / len(X)

    return grad

最终预测准确率为：

accuracy = 99%

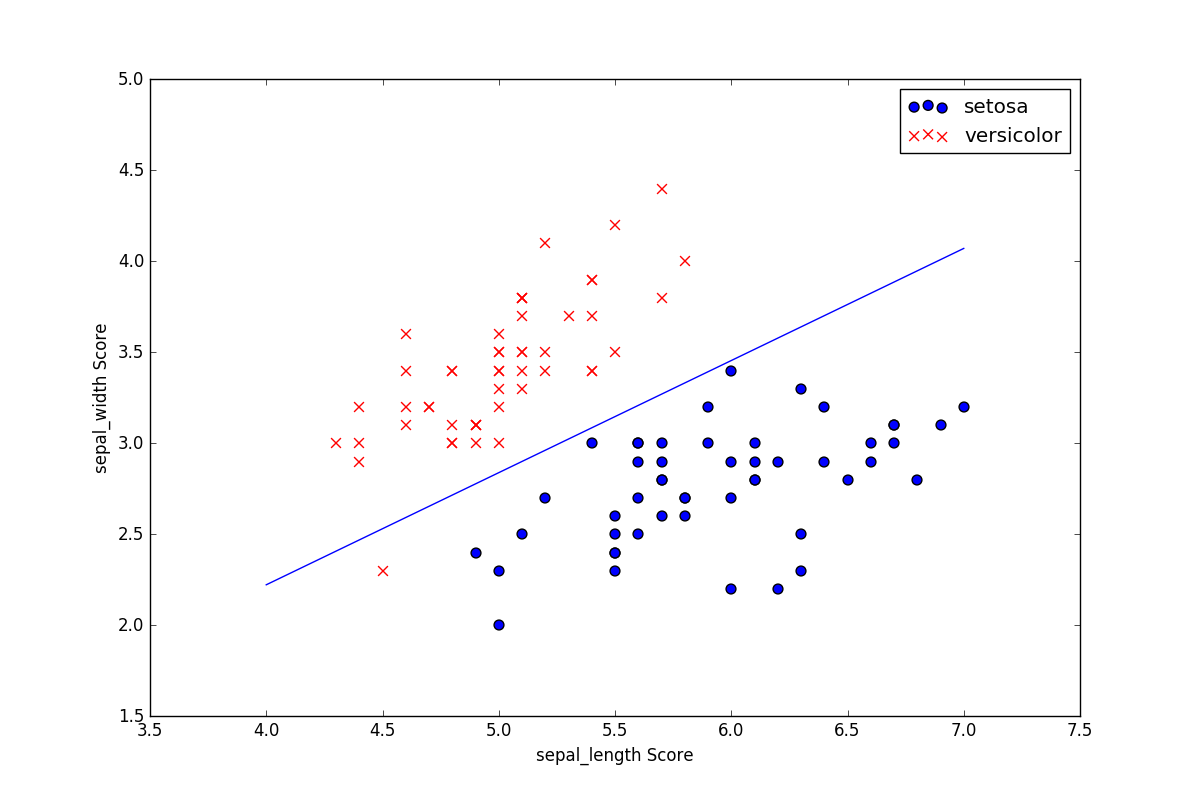
结果分类的图像为：

数据和代码下载请关注公众号【 机器学习和大数据挖掘 】，后台回复【 机器学习 】即可获取