【机器学习】算法原理详细推导与实现(一):线性回归

【机器学习】算法原理详细推导与实现(一):线性回归

今天我们这里要讲第一个有监督学习算法，他可以用于一个回归任务，这个算法叫做 线性回归

房价预测

假设存在如下 m 组房价数据：

面积(m^2)	价格(万元)
82.35	193
65.00	213
114.20	255
75.08	128
75.84	223
...	...

通过上面的数据，可以做出如下一个图。横坐标是 面积(m^2)，纵坐标是 价格(万元)：

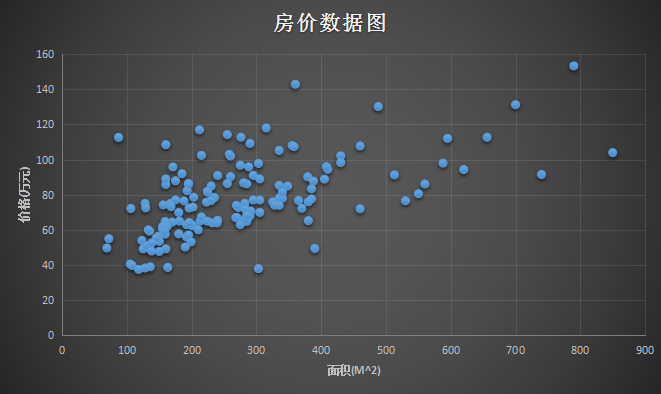
那么问题来了，给你这样一组数据，或者给你这样一个训练数据的集合，能否预测房屋的面积大小和房价之间的关系？

构建函数

存在如下符号假设：

m 为训练数据
x 为输入特征，即房子的大小
y 为输出结果，即房子的价格
(x, y) 为一个样本，即表格中一行代表一个训练样本
\((x^{(i)}, y^{(i)})\) 为第 i 个训练样本

在监督学习中，我们一般会这样做：

1. 首先找到一个训练集合
2. 提供样本 m 给算法构建学习函数
3. 算法会生成一个学习函数，用 \(h(x)\) 表示
4. 给学习函数提供足够的样本\(x\)，由此输出结果\(y\)

学习函数

graph TD A[训练集合]--"样本m"-->B[学习函数] B[学习函数]--"生成"-->C["h(x)"]

训练函数

graph LR A[输入]--"面积(m^2)"-->B["h(x)"] B["h(x)"]--"价格(万元)"-->C[输出]

为了设计学习算法(学习函数)，假设存在如下函数：

\[h(x)=\theta_0+\theta_1x \]

其中 \(x\) 是一个输入函数，这里代表输入的面积(m^2)，\(h(x)\) 是一个输出函数，这里代表 输出的价格(万元)，\(\theta\) 是函数的参数，是需要根据样本学习的参数。对于如上的学习函数只是一个简单的二元一次方程，只需要两组样本 \((x_0,y_0)，(x_1,y_1)\) 就能将 \(\theta_0,\theta_1\) 学习出来，这是一个很简单的函数，但是这样在实际情况中并非很合理。

但是影响房子价格的因素不仅仅是房子的大小。除了房子的大小之外，假设这里还知道每个房子的房间数量：

面积(m^2)	房间(个)	价格(万元)
82.35	2	193
65.00	2	213
114.20	3	255
75.08	2	128
75.84	2	223
...	...	...

那么我们的训练集合将有第二个特征，\(x_1\)表示房子的面积(m^2)，\(x_2\)表示房子的房间(个)，这是学习函数就变成了：

\[h(x)=\theta_0+\theta_1x_1+\theta_2x_2=h_\theta(x) \]

\(\theta\)被称为参数，决定函数中每个特征\(x\)的影响力（权重）。\(h_\theta(x)\) 为参数为 \(\theta\) 输入变量为\(x\)的学习函数。如果令\(x_0=1\)，那么上述方程可以用求和方式写出，也可以转化为向量方式表示：

\[\begin{split} h_\theta(x)&=\theta_0x_0+\theta_1x_1+\theta_2x_2 \\ &=\sum^2_{i=0}{\theta_ix_i} \\ &=\theta^Tx \\ \end{split} \]

假设存在\(m\)个特征\(x\)，那么上述公式求和可以改成：

\[\begin{split} h_\theta(x)&=\sum^m_{i=0}{\theta_ix_i} \\ &=\theta^Tx \\ \end{split} \]

训练参数

在拥有足够多的训练数据，例如上面的房价数据，怎么选择(学习)出参数\(\theta\)出来？一个合理的方式是使学习函数\(h_\theta(x)\) 学习出来的预测值无限接近实际房价值 \(y\)。假设单个样本误差表示为：

\[j(\theta)=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 \]

我们把 \(j(\theta)\) 叫做单个样本的误差。至于为什么前面要乘\(\frac{1}{2}\)，是为了后面计算方便。

为了表示两者之间的接近程度，我们可以用训练数据中所有样本的误差的和，所以定义了 损失函数 为：

\[\begin{split} J(\theta)&=j_1(\theta)+j_2(\theta)+...+j_m(\theta) \\ &=\frac{1}{2}\sum^m_{i=1}{(h_\theta(x^{(i)})-y^{(i)})^2} \\ \end{split} \]

而最终的目的是为了使误差和 \(min(J(\theta))\) 最小，这里会使用一个搜索算法来选取 \(\theta\) 使其误差和无限逼近 \(J(\theta)\) 最小，其流程是：

1. 初始化一组向量 \(\vec{\theta}=\vec{0}\)
2. 不断改变 \(\theta\) 的值使其 \(J(\theta)\) 不断减小
3. 直到取得 \(J(\theta)\) 最小值，活得得到最优的参数向量 \(\vec{\theta}\)

该搜索算法为 梯度下降，算法的思想是这样的，下图看到显示了一个图形和坐标轴，图像的高度表示误差和 \(J(\theta)\)，而下面的两条坐标表示不同的参数 \(\theta\) ，这里为了方便看图只是显示了 \(\theta_0\) 和 \(\theta_1\) ，即变化参数 \(\theta_0\) 和 \(\theta_1\) 使其误差和 \(J(\theta)\) 在最低点，即最小值。

首先随机选取一个点 \(\vec{\theta}\) ，它可能是 \(\vec{0}\) ，也可能是随机的其他向量。最开始的 + 字符号表示开始，搜索使其 \(J(\theta)\) 下降速度最快的方向，然后迈出一步。到了新的位置后，再次搜索下降速度最快的方向，然后一步一步搜索下降，梯度下降算法是这样工作的：

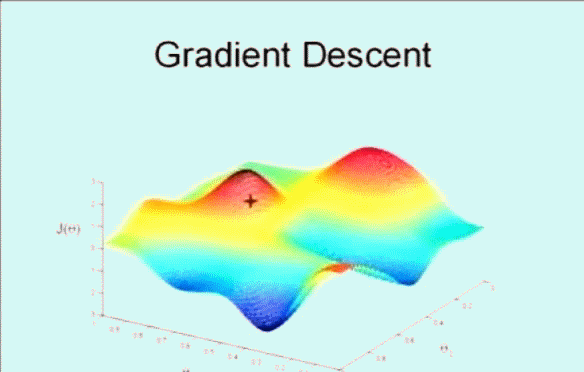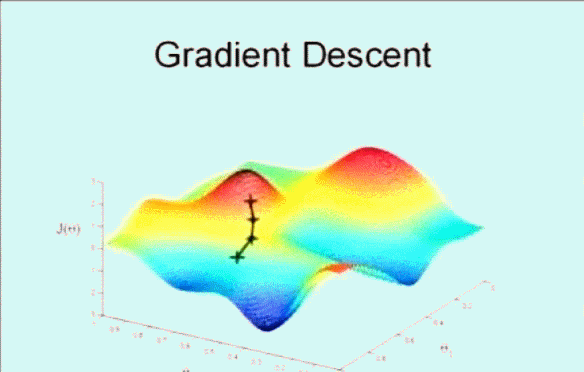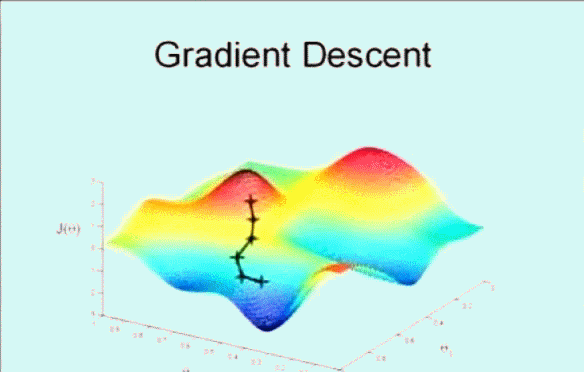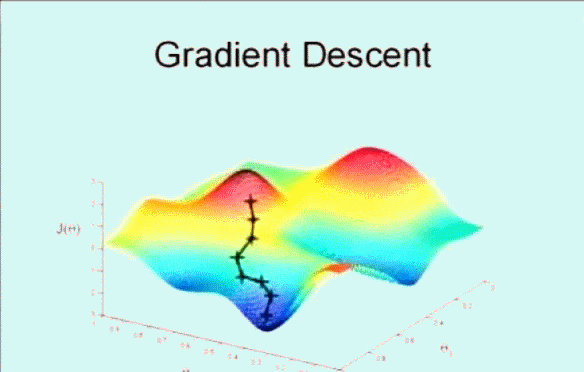
梯度下降的核心就在于每次更新 \(\theta\) 的值，公式为：

\[\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial\theta_j}\tag{1} \]

上面公式代表：\(\theta_j\) 每次都按照一定的 学习速率 \(\alpha\) 搜索使误差和 \(J(\theta)\) 下降最快的方向更新自身的值。而 \(\frac{\partial J(\theta)}{\partial\theta_j}\) 是 \(J(\theta)\) 的偏导值，求偏导得到极值即是下降最快的方向。假设在房价的例子中，只存在一组训练数据 \((x,y)\)，那么可以推导如下公式：

\[\begin{split} \frac{\partial J(\theta)}{\partial\theta_j}&=\frac{\partial}{\partial\theta_j}\frac{1}{2}(h_{\theta}(x)-y)^2 \\ &=2\frac{1}{2}(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(h_{\theta}(x)-y) \\ &=(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(\sum^m_{i=0}{\theta_ix_i}-y) \\ &=(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(\theta_0x_0+\theta_1x_1+...+\theta_mx_m-y) \\ &=(h_{\theta}(x)-y)x_j \\ \end{split}\tag{2} \]

结合 \((1)(2)\) 可以得到：

\[\theta_j:=\theta_j-\alpha(h_{\theta}(x)-y)x_j\tag{3} \]

对于存在 \(m\) 个训练样本，\((1)\) 转化为：

\[\theta_j:=\theta_j-\sum^m_{i=1}\alpha(h_{\theta}(x^{(i)})-y^{(i)})x_j\tag{4} \]

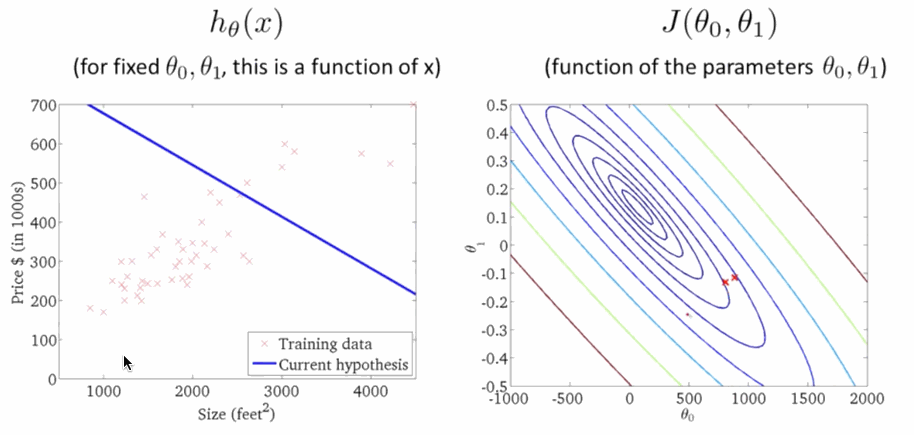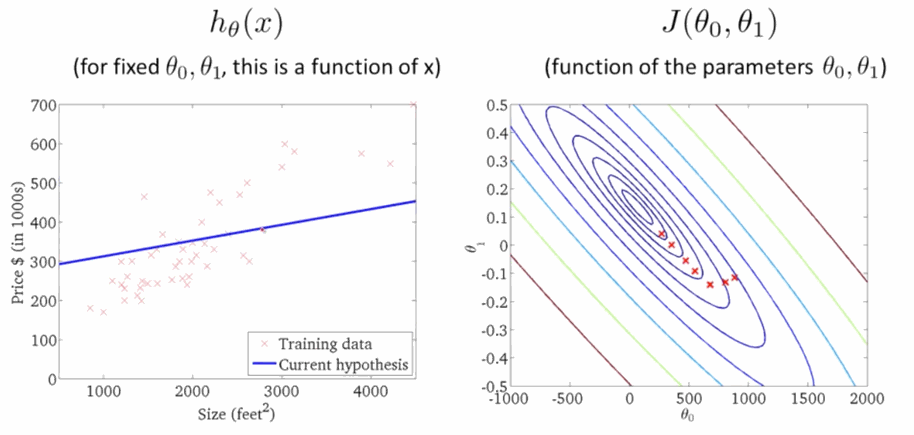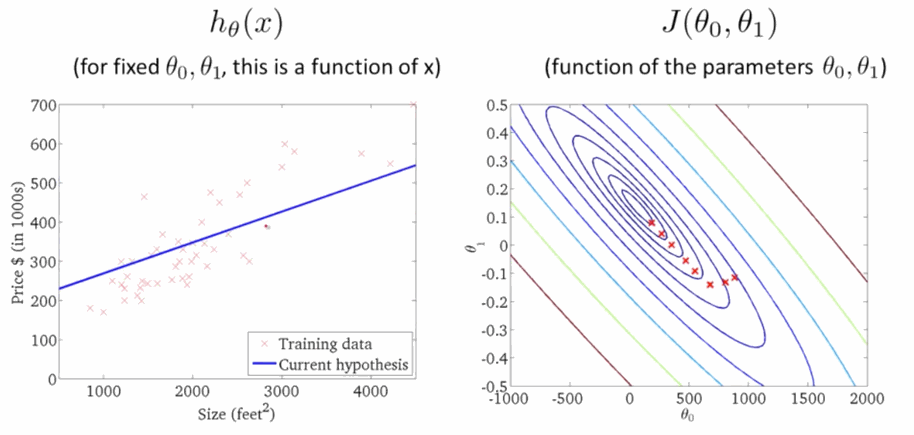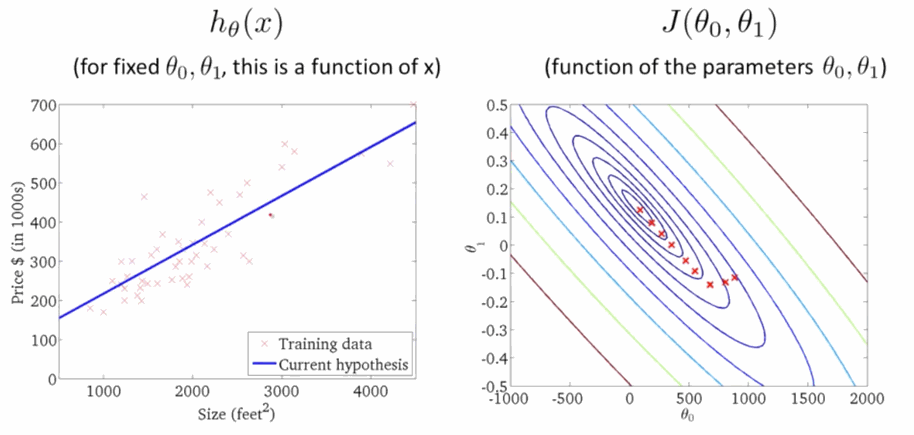
学习速率 \(\alpha\) 是梯度下降的速率，\(\alpha\) 越大函数收敛得越快，\(J(\theta)\) 可能会远离最小值，精度越差；\(\alpha\) 越小函数收敛得越慢，\(J(\theta)\) 可能会靠近最小值，精度越高。下面就是下降寻找最小值的过程，在右图 \(J(\theta)\) 越来越小的时候，左边的线性回归越来准：

代码

选取得到的 150条二手房 数据进行预测和训练，拟合情况如下：

计算损失函数：

# 损失函数
def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

梯度下降函数为：

# 梯度下降函数
def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y

        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

训练迭代1000次后得到参数 \(\theta\)：

# 训练函数
def train_function():
    X, y, theta = get_training_dataset()
    # 有多少个x就生成多少个theta
    theta = np.matrix(np.zeros(X.shape[-1]))
    # 查看初始误差
    # first_cost=computeCost(X, y, theta)
    # print(first_cost)
    # 设置参数和步长
    alpha = 0.01
    iters = 1000

    # 训练得到theta和每一次训练的误差
    g, cost = gradientDescent(X, y, theta, alpha, iters)
    computeCost(X, y, g)
    return g, cost

数据和代码下载请关注公众号【 机器学习和大数据挖掘 】，后台回复【 机器学习 】即可获取