基于漫威系列电影好看程度排序

引申问题

在选择电影时，如果热门电影A有 10000 人观众打分，冷门电影B有 100 个人打分，他们的豆瓣评分都是 8.0 分，怎么比较两部电影的好坏？平时我们都有一种感觉，很多人去评价，这个东西就更可信，只有一两个人说好，可能是托，那么感觉上是电影A更好。

再例如《漫威》系列电影中，距离《复仇者联盟4》上映一周，豆瓣分都是 8.1 分的《钢铁侠》和《复仇者联盟3》，《钢铁侠》有 353695 人评价打分，《复仇者联盟3》有 557491 人评价打分，这两部电影是否一样好看？

贝叶斯平均

截止至 2019/4/27 ，漫威系列 21 部电影按照豆瓣评分如下排序：

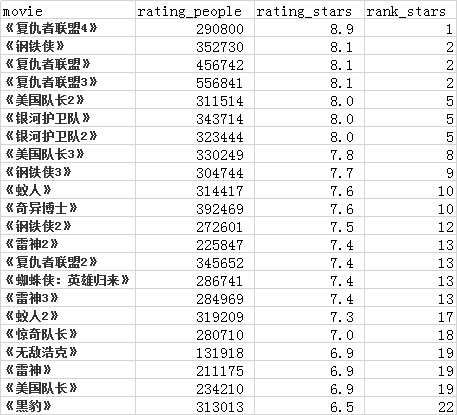
排名第一的是预售票房破7亿《复仇者联盟4》，准确来说这还不是 很严谨 的对比。一个合理的思路是，如果要比较两部电影的好坏，至少应该请同样多的观众观看和评分。既然《钢铁侠》的观众人数偏少，那么应该设法为它 “增加” 一些观众。

贝叶斯平均(Bayesian Model Averaging) 是动态建模中融合集合预报信息的统计后处理方法。通俗来讲就是：

能够在不知道结果的情况下，会自己先估计一个值，然后不断用新的信息修正，使得它越来越接近自身正确的值。

贝叶斯平均值公式如下：

\[WR = \frac{v}{v+m}R+\frac{m}{v+m}C=\frac{vR+mC}{v+m} \]

- WR， 加权得分（weighted rating）
- R， 对象现有平均得分。
- v， 参与为这个对象打分的人数。
- m， 全局平均每个对象的评分人数。
- C， 全局平均每个对象的平均得分。

排序逻辑

合理验证《漫威》系列电影的好评排序，按照《漫威》电影时间线获取每一步电影的：电影名、打分的人数、每个星级的占比：

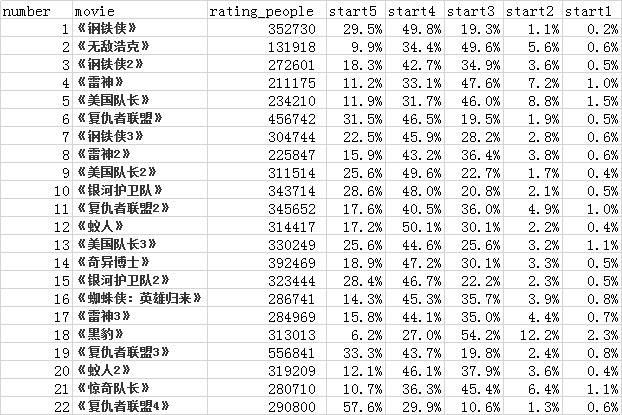
根据公式获取每个电影的平均得分 R、m、 C，计算公式为：

\[R = average\_stars = \frac{rating\_people*start5*5+rating\_people*start4*4+rating\_people*start3*3+rating\_people*start2*2+rating\_people*start1*1}{rating\_people} \]

\[m = average(rating\_people) , C = average(average\_stars) \]

得到最新的 贝叶斯平均排序(rank_bayes) 结果如下所示，和原有的 豆瓣评分排序(rank_stars) 对比如下：

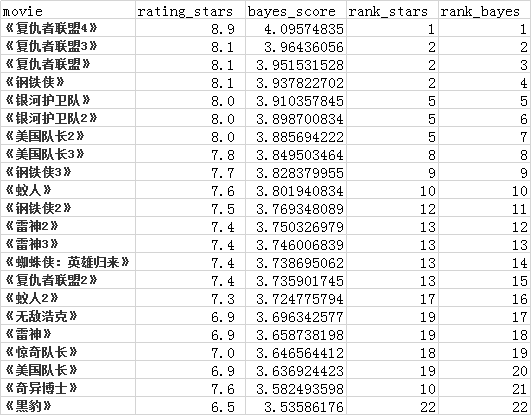
豆瓣分都是 8.1 分的《钢铁侠》和《复仇者联盟3》，《复仇者联盟3》的 贝叶斯平均得分 比 《钢铁侠》好，《复仇者联盟3》比《钢铁侠》好看！

最终的排序是：

《复仇者联盟4》>《复仇者联盟3》>《复仇者联盟》>《钢铁侠》>《银河护卫队》>《银河护卫队2》>《美国队长2》>《美国队长3》>《钢铁侠3》>《蚁人》>《钢铁侠2》>《雷神2》>《雷神3》>《蜘蛛侠：英雄归来》>《复仇者联盟2》>《蚁人2》>《无敌浩克》>《雷神》>《惊奇队长》>《美国队长》>《奇异博士》>《黑豹》

*彩蛋：豆瓣分除以2就是每个电影的平均得分 R *

贝叶斯平均代码

# 计算对象现有平均分
def average_stars_apply(rating_people,start5,start4,start3,start2,start1):
    average_stars = (rating_people*start5*5+rating_people*start4*4+rating_people*start3*3+rating_people*start2*2+rating_people*start1*1)/rating_people
    return round(average_stars,2)

# 计算贝叶斯平均
def bayes_score_apply(R,v,m,C):
    return (v*R+m*C)/(v+m)

# 主函数
def bayes_score(dataFrame):
    df = dataFrame.copy()
    df["average_stars"] = dataFrame.apply(lambda row: average_stars_apply(row['rating_people'], row['start5'],row['start4'], row['start3'],row['start2'],row['start1']), axis=1)
    m = df.mean().rating_people
    C = df.mean().average_stars
    df["bayes_score"] = df.apply(lambda row: bayes_score_apply(row['average_stars'], row['rating_people'], m, C), axis=1)
    return df

计算结果：

拓展场景

在 淘宝天猫 的商品评价下，有对某家店铺的评价等级，在用户购买量不对等，但是评分却一样的情况下，计算竞品 商品 、店铺 在用户眼里的排序：

随意找到两家卖男装的店铺A和店铺B，他们的评分如下所示：

他们的店铺评分一样都是 4.8 分，店铺A的评价人数是 450787，店铺B的评价人数是 198491 ，感觉店铺A评价人多一点感觉可信一些 ，那么有如下条件：

\[R_A=\frac{450787*0.8984*5+450787*0.0536*4+450787*0.0248*3+450787*0.0058*2+450787*0.0174*1}{450787}=4.8098 , v_A=450787 \]

\[R_B=\frac{198491*0.9240*5+198491*0.0366*4+198491*0.0172*3+198491*0.0051*2+198491*0.0171*1}{198491}=4.8453 , v_B=198491 \]

\[m=\frac{450787 +198491}{2}=324639 , C=\frac{4.8098+4.8453}{2}=4.82755 \]

将上述数值带入公式计算得到：

\[WR =\frac{vR+mC}{v+m} \]

\[WR_A = \frac{v_A*R_A+m*C}{v_A+m} = \frac{450787 *4.8098 +324639 *4.82755}{450787 +324639 }=4.81723119556218 \]

\[WR_B = \frac{v_B*R_B+m*C}{v_B+m} = \frac{198491 *4.8453 +324639 *4.82755}{198491 +324639 }=4.83428487517443 \]

实时证明：店铺B优于店铺A ，店铺B虽然评价的人数少，但是好评上还是比店铺A多，整体比店铺A好

缺陷

假设：电影A有10个观众评分，5个为五星，5个为一星；电影B也有10个观众评分，都给了三星，这两部电影在贝叶斯分数是一样的，即：

\[R_A=\frac{5*5+5*1}{10}=3 , R_B=\frac{10*3}{10}=3 , m=\frac{10+10}{2}=10, C=\frac{3+3}{2}=3 \]

\[WR_A = \frac{v_A*R_A+m*C}{v_A+m} = \frac{10*3+10*3}{10+10}=3 \]

\[WR_B = \frac{v_B*R_B+m*C}{v_B+m} = \frac{10*3+10*3}{10+10}=3 \]

计算结果完全一样！

结论

豆瓣评分主要是依据平均分所得，当在评价人数不同但是豆瓣分一样的情况下，就可以使用贝叶斯评分继续判别电影的好坏

下载

关注公众号【机器学习和大数据挖掘】，回复【漫威】即可下载原始数据和代码