学习笔记 【笛卡尔树】
笛卡尔树
笛卡尔树是一种特定的二叉树,可由数列构造,在范围最值查询、范围 \(top k\) 查询 \((range top k queries)\)等问题上有广泛应用。它具有堆的有序性,中序遍历可以输出原数列。——摘自百度百科
笛卡尔树每一个结点由一个键值二元组 \(k\) 构成。要求 \(k\) 满足二叉搜索树的性质,而 \(v\) 满足堆的性质。如图:
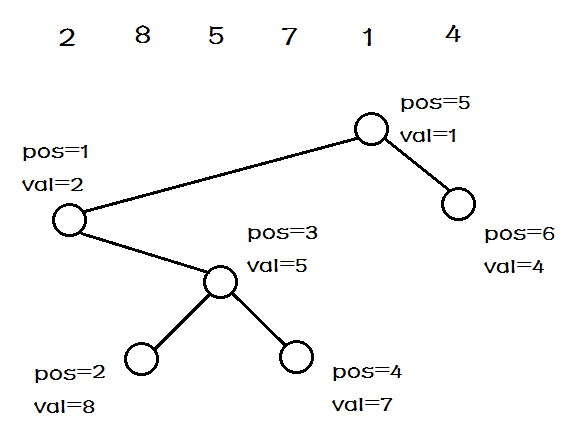
笛卡尔树有这样的性质:
对于树上的任何一个节点 \(x\) 和左右儿子 \(ls\) 和 \(rs\) 有:
- \(pos[\,ls\,]<pos[\,x\,]<pos[\,rs\,]\) 。
- \(val[\,x\,]<val[\,ls\,],val[\,rs\,]\) (大根堆时相反)。
即一棵笛卡尔树的 \(pos\) 满足二叉查找树, \(val\) 满足堆。
笛卡尔树的建树过程:
我们优先满足 \(pos\) 即按顺序依次插入,并调整树的结构,使之满足堆的性质。
所以我们要让新插入的点 \(x\) 在这棵树的最右面,沿着树根向右儿子走分两种情况:
- 这条链上 \(val\) 都比 \(val[\,x\,]\) 小(小根堆,大根堆相反),那么就让 \(x\) 作为最后一个点的右儿子。
- 找到了一个点 \(y\) \(val[\,y\,]>val[\,x\,]\) 此时为了满足堆的性质,\(y\) 必须作为 \(x\) 的儿子且必须是左儿子。
我们使用单调栈来维护笛卡尔树最右儿子链 \(val\) 的递增(递减)性。
建树过程的具体实现:

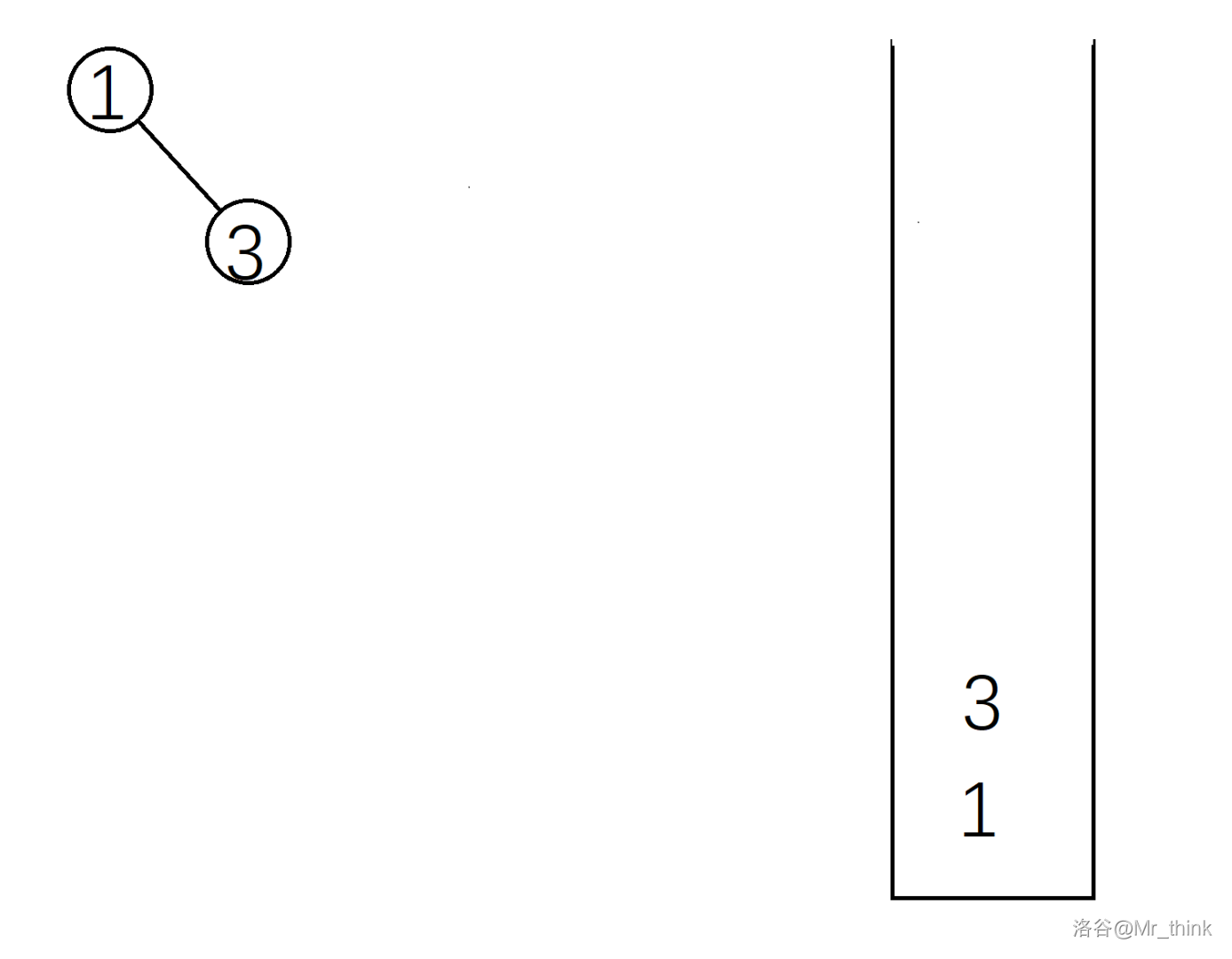
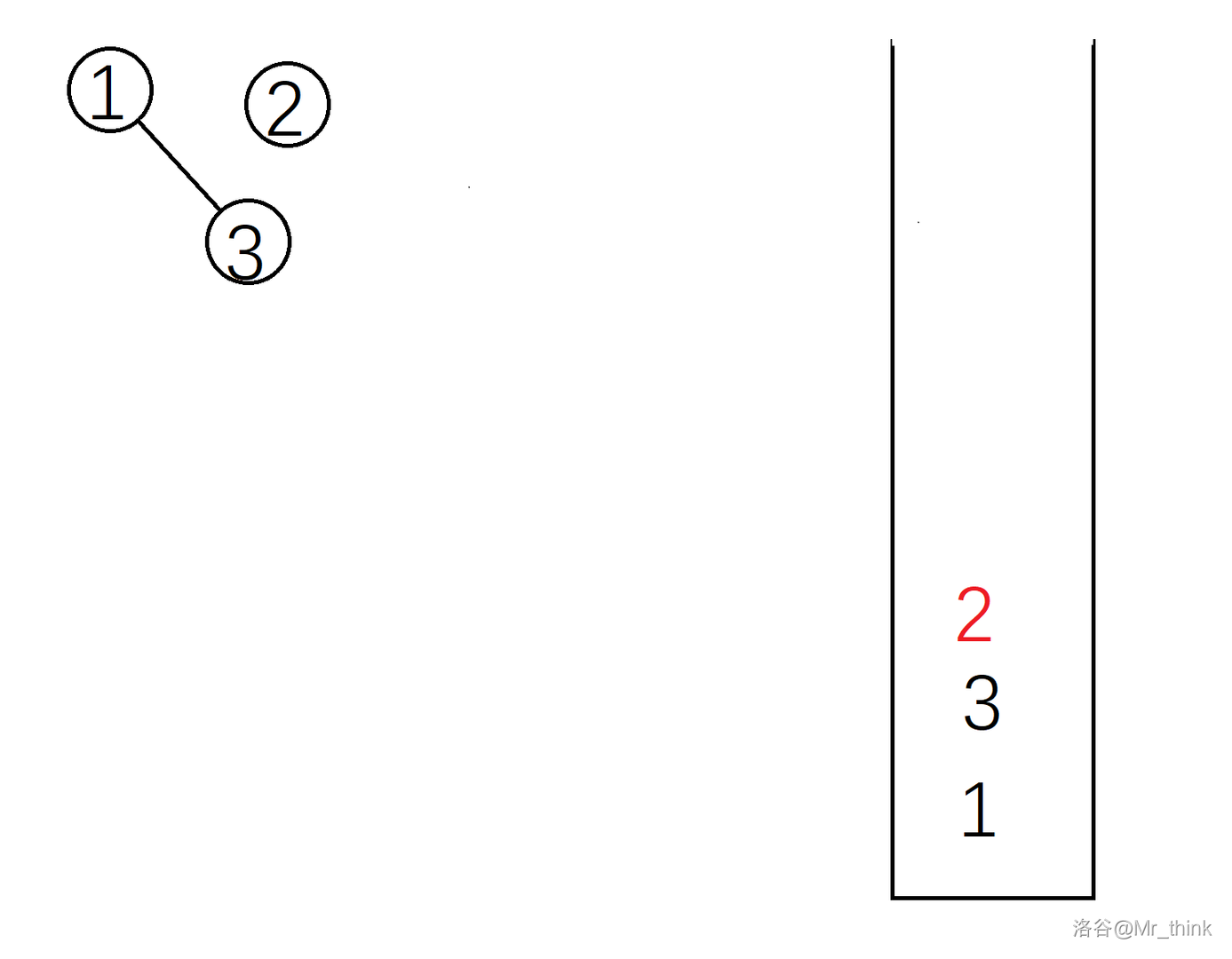
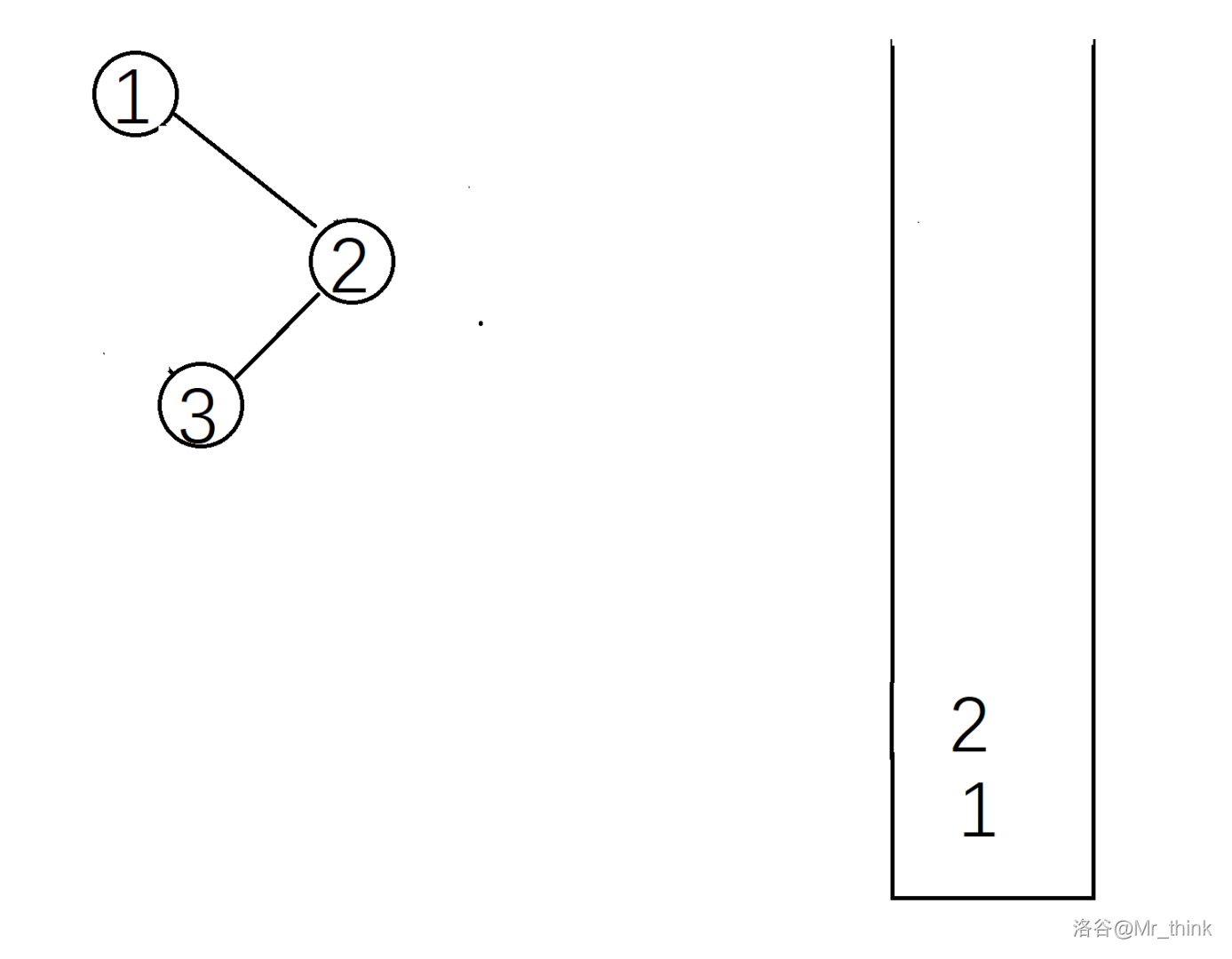

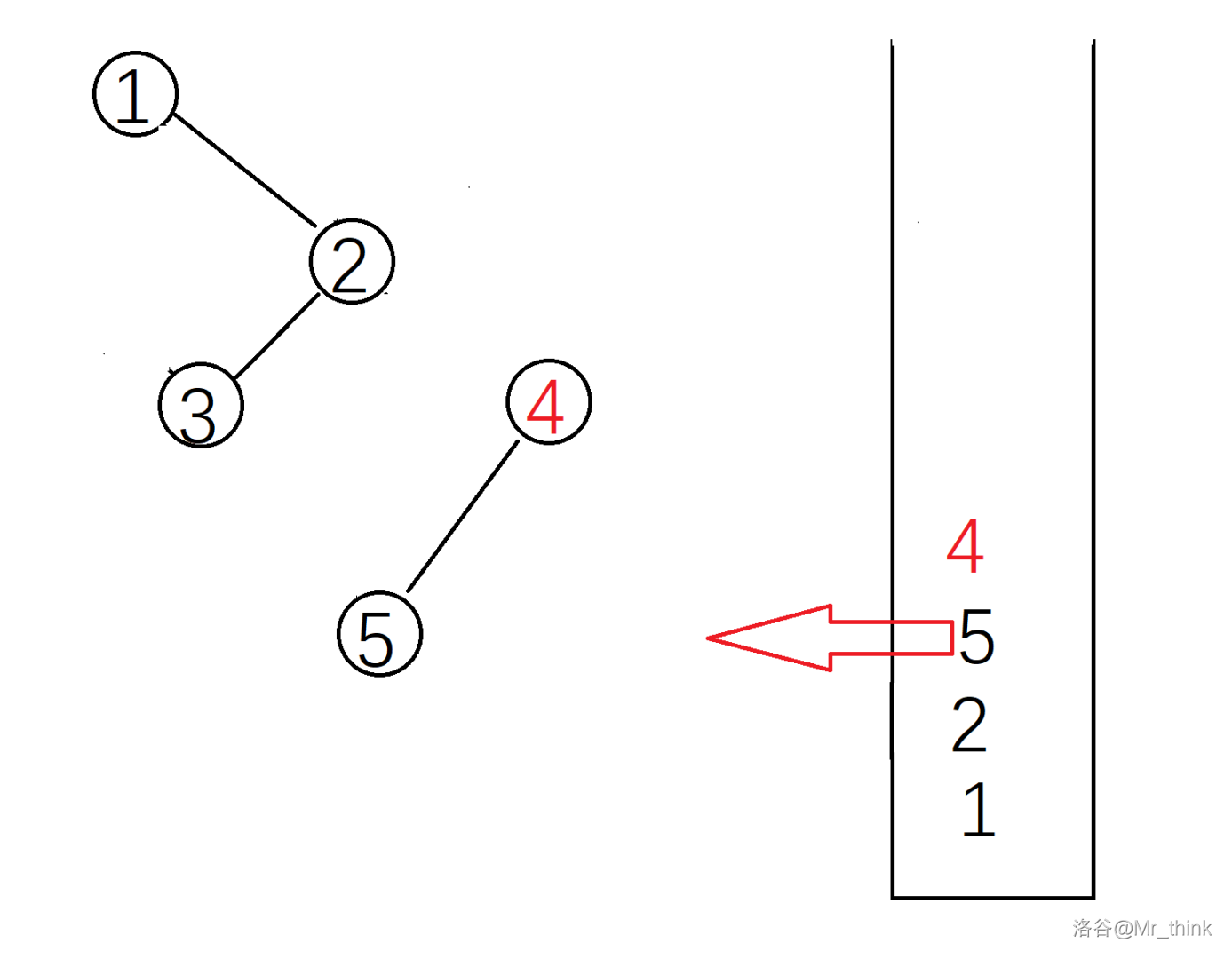
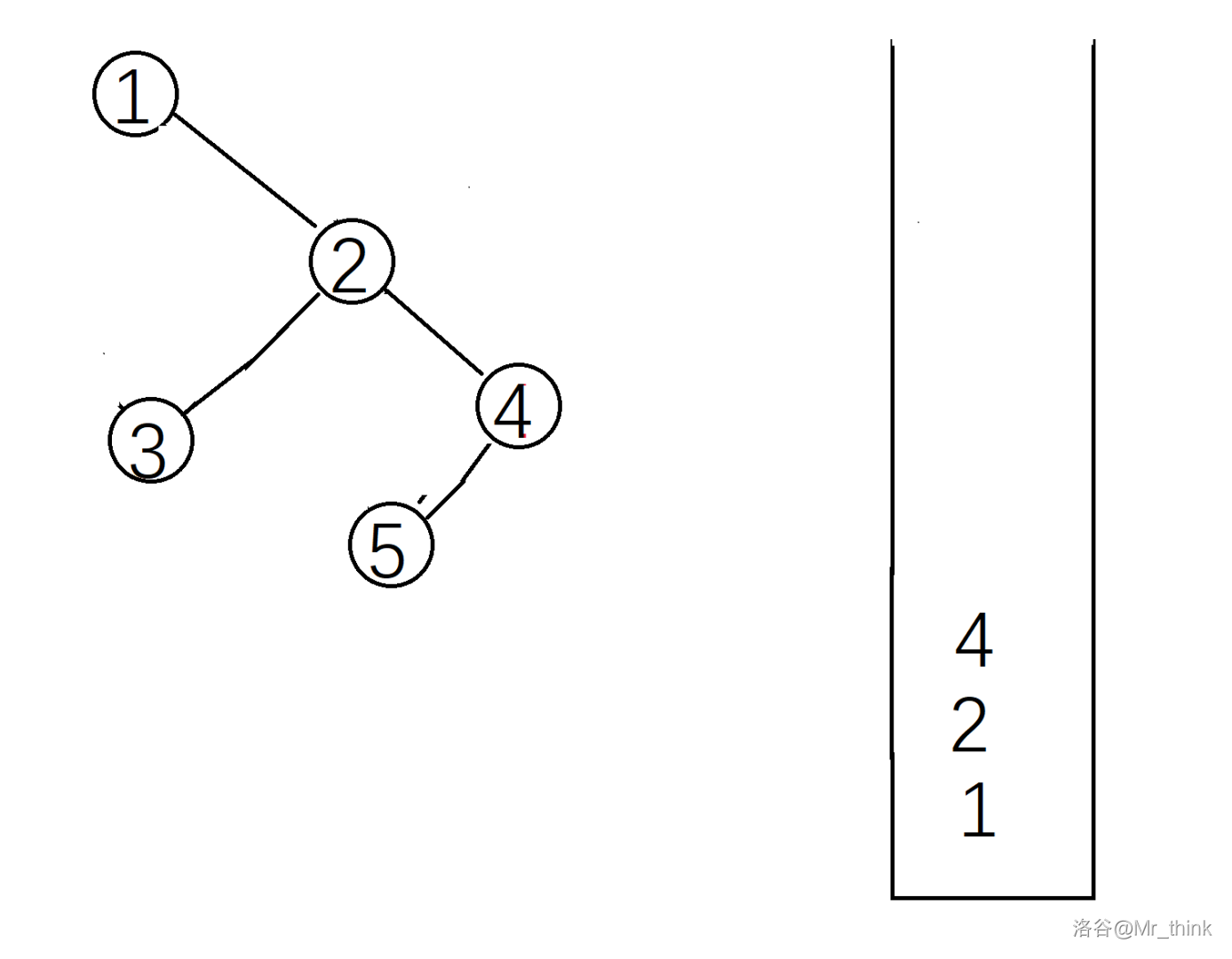
这样一棵笛卡尔树就建好了。
代码
#include<cstdio>
using namespace std;
typedef long long LL;
const int N=1e7+5;
int n;
int a[N];
int st[N],top;
int ls[N],rs[N];
inline void build(){
for(int i=1;i<=n;i++){
while(top&&a[st[top]]>a[i])
ls[i]=st[top--];
rs[st[top]]=i;
st[++top]=i;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build();
LL lans=0,rans=0;
for(int i=1;i<=n;i++)
lans^=(LL)i*(ls[i]+1),rans^=(LL)i*(rs[i]+1);
printf("%lld %lld",lans,rans);
return 0;
}
笛卡尔树的功能:
最简单的一个应用是求元素的左右延伸区间。根据笛卡尔树的性质, \(x\) 一定是 \(x\) 的子树中 \(val\) 最小的(小根堆)。这样我们再对树进行中序遍历,记录下 \(x\) 子树中最左最右的 \(pos\) 即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号