【杂题合集】其真无码邪？

杂题合集

十月份了，该开新篇了

标题党去死

P1407 [国家集训队]稳定婚姻

题目概述：

我们这里有 $n$ 对 $CP$，但是他们之间的关系可能很胃疼很白学，所以有 $m$ 对曾经的 $CP$。设第 $i$ 对 $CP$ 的男方为 $B_i$，女方为 $G_i$，若男 $B_i$ 与女 $G_j$ ($i ≠ j$) 曾交往过，当 $B_i$ 与 $G_i$ 闹矛盾了，$B_i$ 就有可能去找 $G_j$ 寻求安慰。
比如北原春希和小木曾雪菜是 $CP$，但他们当产生矛盾时，北原春希会去找冬马和纱寻求安慰。
再比如说仲上真一郎和汤浅比吕美闹掰了，于是仲上真一郎去找石动乃绘寻求安慰；同时，汤浅比吕美也去找到了石动纯；这样原本的两对 $CP$（兄妹）就被拆开了，但是又组成了两对新的 $CP$（我是养鸡党），我们称这样的关系是不稳定的。

简而言之，若在 $B_i$ 和 $G_i$ 闹掰的前提下，这 $2n$ 个人仍然能组成 $n$ 对 $CP$，那么关系 $i$ 就是不稳定的，否则，关系 $i$ 就是稳定的。

需要判断每对关系是不是稳定的。

真TM难概括，艹

题解

如果 $CP$ 关系是 Unsafe 的，那么这几个人的关系一定是一个环。

以样例2为例：

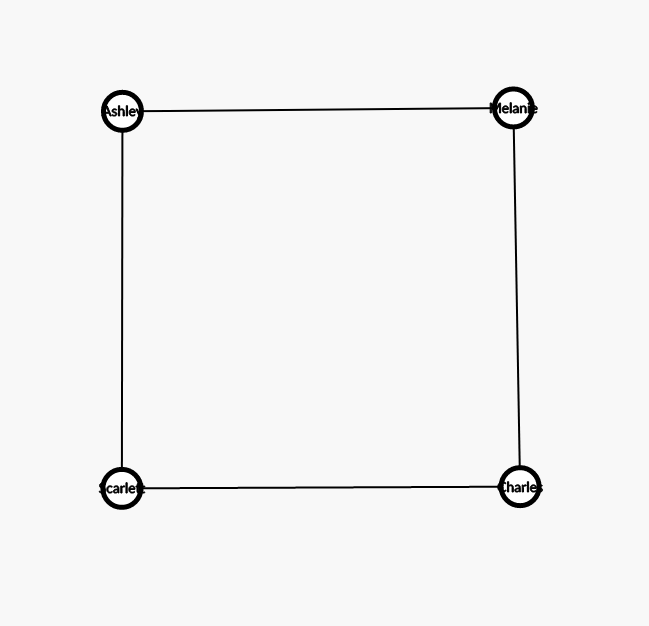
四个人形成了一个不具稳定关系的四边形，所以两对 $CP$ 都是不稳定的。

而样例1：

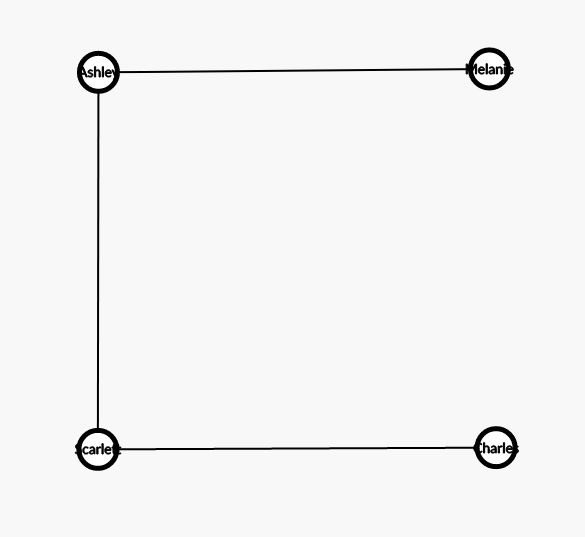
没有形成环，两对 $CP$ 都是稳定的。

每一个环都是一个强连通分量，所以可以想到tarjan来求强连通分量，
然后问题就是如何建图了，不难想到可以建无向边，但是无向图没法跑这个，那考虑 $CP$ 和前 $CP$ 分开连边。$CP$ 从女到男连边，前 $CP$ 从男到女连边。为什么？考虑传递性。我们假定每次 $CP$ 关系破裂后，男方 $B_i$ 先去找前 $CP$ $G_j$。然后像多米诺骨牌一样的传递，$G_j$ 传递给 $B_j$，两人关系破裂，$B_j$ 再去找 $G_k$......以此类推。

所以，当 $CP$ 双方在同一个强连通分量中，那这对关系是不稳定的，反之稳定。

Code

点击查看代码

#include<set>
#include<string>
#include<iostream>
#include<algorithm>
#include<unordered_map>
 
using namespace std;
 
const int MAXN = 4010;
int n, m, cnt, sit, num, tot;
int head[MAXN << 1], low[MAXN << 1], dfn[MAXN << 1], belong[MAXN << 1];
bool vis[MAXN << 1];
int stk[MAXN << 1], top;
string boy[MAXN], girl[MAXN];
unordered_map< string, int > pos;
 
struct Edge{
    int to, next;
}e[MAXN * MAXN];
 
inline void Add(int u, int v){
    e[++cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
 
void Tarjan(int u){
    low[u] = dfn[u] = ++num;
    vis[u] = true;
    stk[++top] = u;
 
    for(register int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(!dfn[v]){
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(vis[v]) low[u] = min(low[u], dfn[v]);
    }
 
    if(low[u] == dfn[u]){
        ++tot;
        int t;
        do{
            t = stk[top--];
            vis[t] = false;
            belong[t] = tot;
        }while(t != u);
    }
}
 
int main(){
    ios :: sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
 
    cin >> n;
    for(register int i = 1; i <= n; i++){
        int u = ++sit, v = ++sit;
        cin >> girl[i] >> boy[i];
        Add(u, v);
        pos[girl[i]] = u, pos[boy[i]] = v;
    }
 
    cin >> m;
    for(register int i = 1; i <= m; i++){
        string g, b;
        cin >> g >> b;
        int u = pos[g], v = pos[b];
        Add(v, u);
    }
 
    for(register int i = 1; i <= sit; i++)
        if(!dfn[i]) Tarjan(i);
    
    for(register int i = 1; i <= n; i++){
        int u = pos[girl[i]], v = pos[boy[i]];
        if(belong[u] != belong[v]) puts("Safe");
        else puts("Unsafe"); 
    }
 
    return 0;
}