【学习笔记/模板】笛卡尔树

笛卡尔树

笛卡尔树是一种特定的二叉树数据结构，可由数列构造，在范围最值查询、范围top k查询（range top k queries）等问题上有广泛应用。它具有堆的有序性，中序遍历可以输出原数列。笛卡尔树结构由Vuillmin(1980)在解决范围搜索的几何数据结构问题时提出。从数列中构造一棵笛卡尔树可以线性时间完成，需要采用基于栈的算法来找到在该数列中的所有最近小数。——百度百科

百度百科真能扯。

概述

笛卡尔树是一种二叉树，每个节点由一个键值二元组 \((k, w)\) 组成。其中 \(k\) 要求满足二叉搜索树的性质，\(w\) 要求满足堆的性质。

一个性质：如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 互不相同，那么这个笛卡尔树的结构是唯一的。

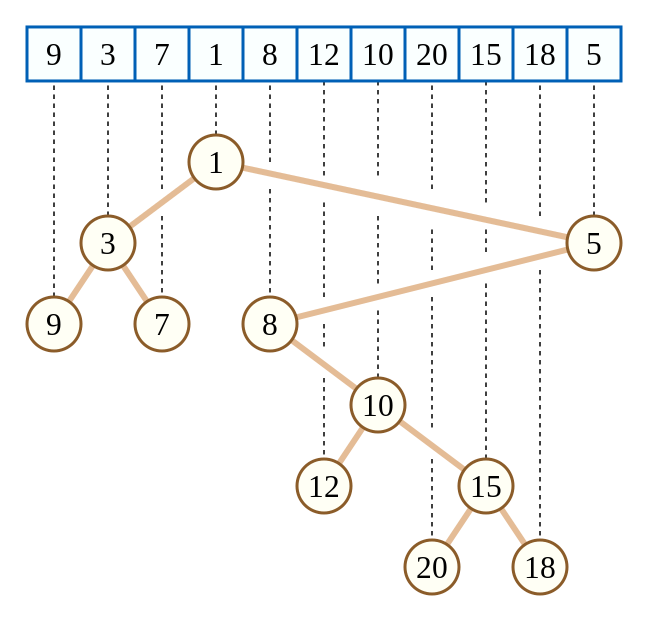
如图，这颗笛卡尔树以数组元素为键值 \(w\)，以数组下标为键值 \(k\)。不难发现 \(k\) 满足 \(BST\) 的性质，\(w\) 满足小根堆。

其实上图的笛卡尔树是一种特殊的情况，键值 \(k\) 正好对应数组下标，于是一棵子树内的下标是连续的一个区间（这样才能满足二叉搜索树的性质）。

构建

考虑将元素按照键值 \(k\) 升序排序，然后一个个插入当前的笛卡尔树中。由于 \(k\) 要满足 \(BST\) 的性质，新插入的元素必然在树的右链的末端（右链：从根节点一直往右儿子走，经过的节点形成的链）。

于是进行这样的一个过程，从下往上比较右链节点与当前节点 \(u\) 的 \(w\)，若找到了一个右链上的节点 \(x\)，满足 \(x_w < u_w\)，就把 \(u\) 接到 \(x\) 的右儿子上，原本 \(x\) 的右子树变成 \(u\) 的左子树。

如图，红框就是我们维护的右链。

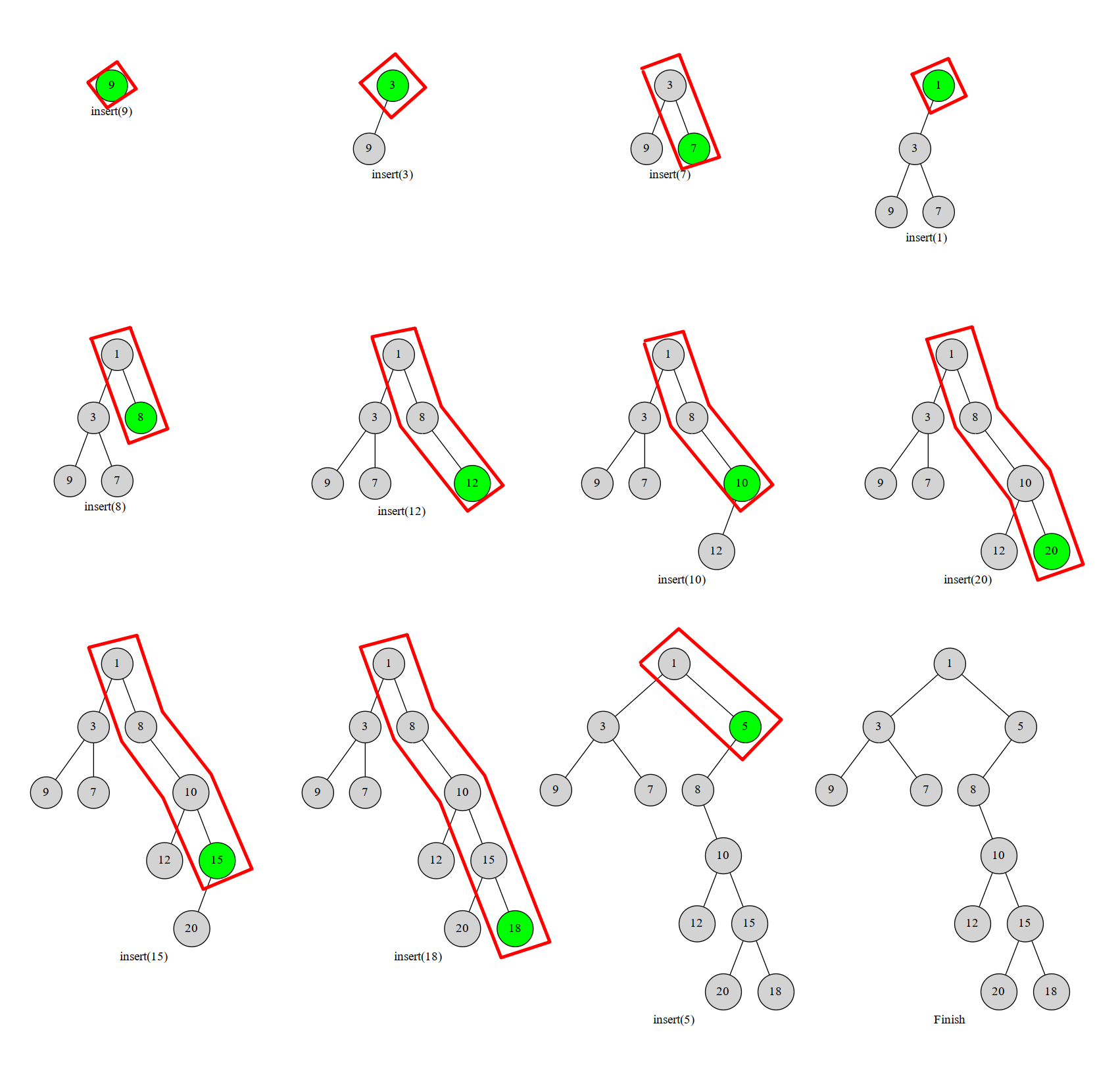
每个数最多进出右链一次，可以用单调栈维护。栈中维护当前笛卡尔树中的右链上的节点，当一个点不在右链上了就把它弹掉，复杂度 \(O(n)\)。最后的栈底元素就是笛卡尔树的根节点。

void Build(){
    top = 0; //清空栈，top表示操作前的栈顶
    for(register int i = 1; i <= n; i++){
        tr[i].key = i, tr[i].val = num[i];
        int res = top; //res 表示当前栈顶
        while(res && tr[stk[res]].val > tr[i].val)
	//如果栈顶元素 > 当前元素 不满足小根堆的性质，将栈顶元素弹栈，直到找到小于等于当前元素的值
            --res;

        if(res) tr[stk[res]].ch[1] = i;
	//如果栈中还有元素，那当前元素是栈顶元素的右儿子
        if(res < top) tr[i].ch[0] = stk[res + 1];
	//如果当前的栈顶 < 操作前的栈顶，表明被弹出的元素会构成当前元素的左子树

        stk[++res] = i; //当前元素入栈
        top = res;
    }

    root = stk[1]; //栈底元素就是根节点
}

例题

P5854 【模板】笛卡尔树

模板题，直接上码了。

#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1e7 + 10;
int n;
long long lans, rans;
int num[MAXN];
int stk[MAXN], top;

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

struct Cartesian_Tree{
    int root;

    struct Tree{
        int key;
        int val;
        int ch[2];
    }tr[MAXN];

    void Build(){
        top = 0;
        for(register int i = 1; i <= n; i++){
            tr[i].key = i, tr[i].val = num[i];
            int res = top;
            while(res && tr[stk[res]].val > tr[i].val)
                --res;

            if(res) tr[stk[res]].ch[1] = i;
            if(res < top) tr[i].ch[0] = stk[res + 1];

            stk[++res] = i;
            top = res;
        }

        root = stk[1];
    }
}C;

int main(){
    n = read();
    for(register int i = 1; i <= n; i++)
        num[i] = read();
    
    C.Build();

    for(register int i = 1; i <= n; i++){
        lans ^= 1LL * i * (C.tr[i].ch[0] + 1);
        rans ^= 1LL * i * (C.tr[i].ch[1] + 1);
    }

    printf("%lld %lld", lans, rans);

    return 0;
}

P1377 [TJOI2011] 树的序

给一个生成序列，建出一棵笛卡尔树，求字典序最小的可以得到相同笛卡尔树的生成序列。

根据二叉搜索树的性质，其先序的字典序最小，所以字典序最小的生成序列就是笛卡尔树的先序遍历。

至于为什么可以用到笛卡尔树，因为这个序列满足二叉搜索树，那么和我们笛卡尔树中的满足二叉搜索树的性质相同。

同时，一个元素越在序列后边，它在二叉搜索树中的位置越深，换句话说，对于一个数 \(x\)，在它到根的路径上的点一定在序列的前面。所以可以把第几个插入看做权值 \(w\) 去构建笛卡尔树。

#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1e5 + 10;
int n;
int num[MAXN];
int stk[MAXN], top;

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

struct Cartesian_Tree{
    int root;

    struct Tree{
        int key;
        int val;
        int ch[2];
    }tr[MAXN];

    void Build(){
        top = 0;
        for(register int i = 1; i <= n; i++){
            tr[i].key = i, tr[i].val = num[i];
            int res = top;
            while(res && tr[stk[res]].val > tr[i].val)
                --res;

            if(res) tr[stk[res]].ch[1] = i;
            if(res < top) tr[i].ch[0] = stk[res + 1];

            stk[++res] = i;
            top = res;
        }

        root = stk[1];
    }

    void Print(int rt){
        if(!rt) return;

        printf("%d ", tr[rt].key);
        Print(tr[rt].ch[0]);
        Print(tr[rt].ch[1]);
    }
}C;

int main(){
    n = read();
    for(register int i = 1; i <= n; i++){
        int x = read();
        num[x] = i;
    }
    
    C.Build();

    C.Print(C.root);

    return 0;
}