【学习笔记】树链剖分系列四——换根操作

前传1：【学习笔记】树链剖分系列一 ——树链剖分（重链剖分）——我是不是应该写一篇树链剖分呢

前传2：【学习笔记】树链剖分系列二——LCA

前传3：【学习笔记】树链剖分系列三——点权转边权

前言

CSP2022 rp++！！！

这个系列算是枯木逢春了，在 CSP 前攒点 rp，写点算造福后人 谁会看啊 的东西。

大家可能没有注意到，这篇我又更了点东西

换根操作
续集3：【学习笔记】树链剖分系列四——换根操作
CF916E Jamie and Tree
P3979 遥远的国度

所以又有续集了。

不过毕竟是续集，来看这篇博客的你相信已经掌握了上边的树链剖分的知识了罢。

正题

一般的树链剖分题会有一个固定的根节点，所以只需要剖一次就能找到所有需要的信息。然而换根操作会改变根节点，从而使原本固定的信息有所变化。

然而，我们肯定不能每换一个根节点就重新剖一次，时间复杂度显然难以接受，那我们能不能只剖一次再依靠固定的信息来进行操作呢？

显然是可以的，我们可以想到树链剖分是靠 dfs 序把一棵树“拍扁”成一段段的序列，再靠线段树来维护。那我们可以靠这个 dfs序来搞事情。

例题/实现

P3979 遥远的国度

我们先以 \(1\) 为根将树剖掉。

首先，我们可以确定的是不论根怎么变，两点之间的路径都不会变，因为树的特性：两点之间的路径是唯一的。

然后，我们就需要考虑询问 \(x\) 的子树最小值在对于不同的根时的各种状况，设当前根为 \(root\)：

  1. \(x = root\)：就是整棵数的最小值，直接输出即可；

    if(x == root) printf("%d\n", S.tr[1].min);

  2. \(x\) 在 \(root\) 的子树中 或者 \(x\) 不在 \(root\) 到 \(1\) 的路径上（\(x\) 在树的其他枝杈上，与 \(root\) 没有亲缘关系）：以 \(root\) 为根亦或以 \(1\) 为根都对 \(x\) 子树的范围没有影响，直接正常查询。

    • 首先，当 \(x\) 在 \(root\) 的子树里时，一定有 dfn[x] > dfn[root]。
    • 然后，当 \(x\) 不在 \(root\) 到 \(1\) 的路径上（\(x\) 在树的其他枝杈上，与 \(root\) 没有亲缘关系）时，有 dfn[x] > dfn[root] + size[root] - 1 或者 dfn[x] + size[x] - 1 < dfn[root]。

    所以，综上有：

    else if(dfn[x] > dfn[root] || dfn[x] + size[x] - 1 < dfn[root])
    printf("%d\n", S.Query_Min(1, dfn[x], dfn[x] + size[x] - 1));

  3. \(x\) 在 \(root\) 到 \(1\) 的路径上：这里是下文讲解的重点 或者说全是 。

我们感性理解一下，如下图：

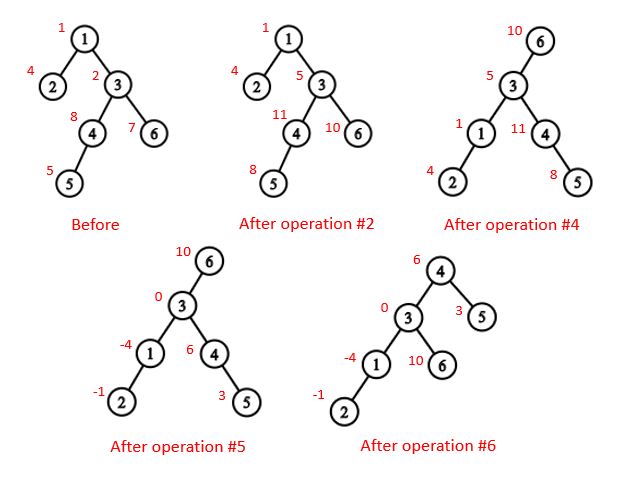
image

图三（第一行第三列）以 \(6\) 为根就是将 \(6\) 一个旱地拔葱，提到根节点的位置，再进行一些“感性的”“父死子继”（父节点和子节点交换位置）。

如果用更正经的语言描述，就是 \(x\) 的孩子中包含 \(root\) 的那个（以下称为 \(ch\)）会变成 \(x\) 的父节点，\(ch\) 兄弟节点不变，仍为 \(x\) 的子节点，同时 \(x\) 的父节点会变成 \(x\) 的子节点，并且这个变化会从 \(x\) 沿 \(x\) 到 \(1\) 的路径，传递给每个路径上的节点。

也就是说，相当于整棵以 \(1\) 为根的树，除去以 \(ch\) 为根的子树，都变成了查询对象。

我们考虑怎么求出这个 \(ch\)。

因为用的是树剖，我们仍先考虑树剖跳链。

每次让深度大的点（称为 \(u\)）向上跳，如果 \(u\) 所在的重链的起点的父节点就是深度小的点（称为 \(v\)），直接返回 \(u\) 所在重链的起点。

跳到最后，\(u\) 节点就变成了 \(u\) 和 \(v\) 的 \(LCA\)，（然而因为 \(u\) 在 \(v\) 的子树中其实就是把 \(u\) 和 \(v\) 换了以下），并且 \(u\) 和 \(v\) 在一条重链上，所以 \(ch\) 就是 \(u\) 的重儿子，因为只有重儿子才会和父节点在一条重链上。

int Get_Son(int x, int y){ 
    while(top[x] != top[y]){
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        if(fa[top[x]] == y) return top[x];
        x = fa[top[x]];
    }

    if(deep[x] > deep[y]) swap(x, y);

    return son[x];
}

之后，要判断 \(ch\) 的子树的范围，如果 \(ch\) 的子树已经到了 \(n\)，就不需要查询 dfn[ch] + size[ch] 到 \(n\) 了。

else{
    int ch = Get_Son(x, root);

    if(dfn[ch] + size[ch] - 1 == n)
        printf("%d\n", S.Query_Min(1, 1, dfn[ch] - 1));
    else printf("%d\n", min(S.Query_Min(1, 1, dfn[ch] - 1), S.Query_Min(1, dfn[ch] + size[ch], n)));
}

Code

#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1e5 + 10;
const int INF = 2147483647;
int n, m, cnt, num, root;
int head[MAXN], dis[MAXN], val[MAXN];
int fa[MAXN], son[MAXN], size[MAXN], deep[MAXN];
int dfn[MAXN], top[MAXN];

struct Edge{
    int to, next;
}e[MAXN << 1];

inline void Add(int u, int v){
    e[++cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

void dfs_deep(int rt, int father, int depth){
    size[rt] = 1;
    fa[rt] = father;
    deep[rt] = depth;

    int max_son = -1;
    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(v == father) continue;

        dfs_deep(v, rt, depth + 1);
        size[rt] += size[v];

        if(max_son < size[v]){
            son[rt] = v;
            max_son = size[v];
        }
    }
}

void dfs_top(int rt, int top_fa){
    dfn[rt] = ++num;
    top[rt] = top_fa;
    val[num] = dis[rt];

    if(!son[rt]) return;
    dfs_top(son[rt], top_fa);

    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(!dfn[v]) dfs_top(v, v);
    }
}

struct Segment_Tree{
    struct Tree{
        int l, r;
        int min;
        int lazy;
    }tr[MAXN << 2];

    inline int lson(int rt){
        return rt << 1;
    }

    inline int rson(int rt){
        return rt << 1 | 1;
    }

    inline void Pushup(int rt){
        tr[rt].min = min(tr[lson(rt)].min, tr[rson(rt)].min);
    }

    inline void Pushdown(int rt){
        if(tr[rt].lazy){
            tr[lson(rt)].min = tr[rt].lazy;
            tr[rson(rt)].min = tr[rt].lazy;
            tr[lson(rt)].lazy = tr[rt].lazy;
            tr[rson(rt)].lazy = tr[rt].lazy;
            tr[rt].lazy = 0;
        }
    }

    void Build(int rt, int l, int r){
        tr[rt].l = l;
        tr[rt].r = r;

        if(l == r){
            tr[rt].min = val[l];
            return;
        }

        int mid = (l + r) >> 1;
        Build(lson(rt), l, mid);
        Build(rson(rt), mid + 1, r);

        Pushup(rt);
    }

    void Update(int rt, int l, int r, int data){
        if(tr[rt].l >= l && tr[rt].r <= r){
            tr[rt].min = data;
            tr[rt].lazy = data;
            return;
        }

        Pushdown(rt);

        int mid = (tr[rt].l + tr[rt].r) >> 1;
        if(l <= mid) Update(lson(rt), l, r, data);
        if(r > mid) Update(rson(rt), l, r, data);

        Pushup(rt);
    }

    int Query_Min(int rt, int l, int r){
        if(tr[rt].l >= l && tr[rt].r <= r)
            return tr[rt].min;
        
        Pushdown(rt);

        int ans = INF;
        int mid = (tr[rt].l + tr[rt].r) >> 1;
        if(l <= mid) ans = min(ans, Query_Min(lson(rt), l, r));
        if(r > mid) ans = min(ans, Query_Min(rson(rt), l, r));

        return ans;
    }
}S;

void Update_Tree(int x, int y, int data){
    while(top[x] != top[y]){
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        S.Update(1, dfn[top[x]], dfn[x], data);
        x = fa[top[x]];
    }

    if(deep[x] > deep[y]) swap(x, y);
    S.Update(1, dfn[x], dfn[y], data);
}

int Get_Son(int x, int y){
    while(top[x] != top[y]){
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        if(fa[top[x]] == y) return top[x];
        x = fa[top[x]];
    }

    if(deep[x] > deep[y]) swap(x, y);

    return son[x];
}

int main(){
    n = read(), m = read();
    for(register int i = 1; i <= n - 1; i++){
        int u, v;
        u = read(), v = read();
        Add(u, v);
        Add(v, u);
    }
    for(register int i = 1; i <= n; i++)
        dis[i] = read();
    
    dfs_deep(1, 0, 1);
    dfs_top(1, 1);
    S.Build(1, 1, n);

    root = read();
    for(register int i = 1; i <= m; i++){
        int opt;
        opt = read();

        if(opt == 1) root = read();
        else if(opt == 2){
            int x, y, v;
            x = read(), y = read(), v = read();
            Update_Tree(x, y, v);
        }
        else{
            int x;
            x = read();

            if(x == root) printf("%d\n", S.tr[1].min);
            else if(dfn[x] > dfn[root] || dfn[x] + size[x] - 1 < dfn[root])
                printf("%d\n", S.Query_Min(1, dfn[x], dfn[x] + size[x] - 1));
            else{
                int ch = Get_Son(x, root);

                if(dfn[ch] + size[ch] - 1 == n)
                    printf("%d\n", S.Query_Min(1, 1, dfn[ch] - 1));
                else printf("%d\n", min(S.Query_Min(1, 1, dfn[ch] - 1), S.Query_Min(1, dfn[ch] + size[ch], n)));
            }
        }
    }

    return 0;
}

还有一道题：

CF916E Jamie and Tree

其中的换根后求 \(LCA\) 操作择日（等明天考完CSP初赛）再更。

考完力，更一下。

对于求 \(x\) 和 \(y\) 在根 \(root\) 下的 \(LCA\)，我们分别讨论下 \(x\)，\(y\)，\(root\)，在以 \(1\) 为根的树中两两之间 \(LCA\) 的关系。（以下 \(x\) 和 \(y\) 在根 \(root\) 下的 \(LCA\) 写作 \(Lca(x, y)\)）

记 \(LCA(x, root) = anc_{xr}，LCA(y, root) = anc_{yr}，LCA(x, y) = anc_{xy}\)。

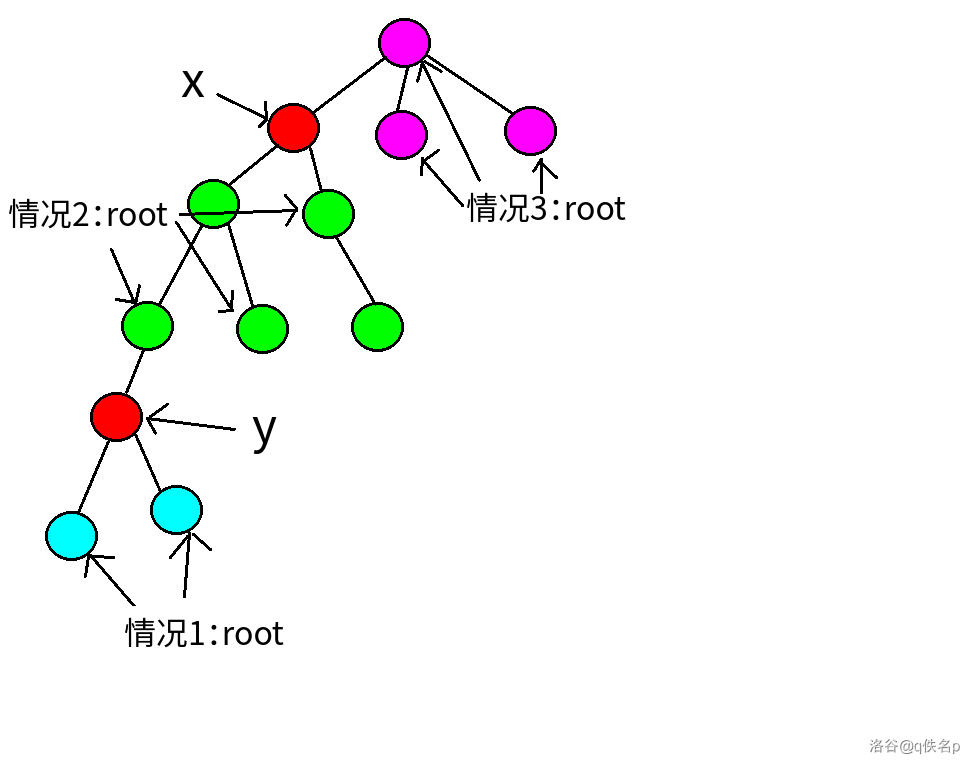
情况①：\(anc_{xy} = x\)（其中 \(x\)，\(y\) 按深度调换，令 deep[x] <= deep[y]）。

如下图：

image

  1. 对应图中的情况 \(1\) ，\(anc_{xr} = x，anc_{yr} = y\)，同时可以发现 \(Lca(x, y) = y\)，得 \(Lca(x, y) = anc_{yr}\)。

  2. 对应图中的情况 \(2\)，\(anc_{xr} = x, anc_{yr} = root\)，\(Lca(x, y) = root\)，即 \(Lca(x, y) = anc_{yr}\)。

  3. 对应图中的情况 \(3\)，\(anc_{xr} = root，anc_{yr} = root\)，\(Lca(x, y) = x\)，即 \(Lca(x, y) = anc_{xy}\)。

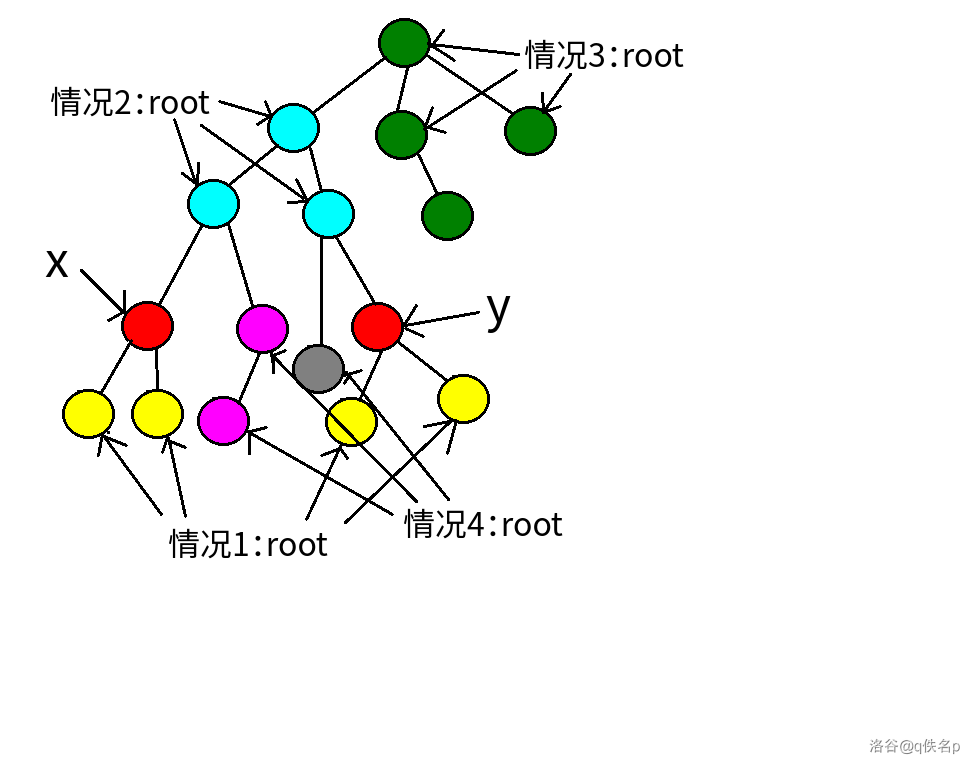
情况②：\(anc_{xy} ≠x\)，同时 \(anc_{xy} ≠ y\)（因为调整了 \(x\) 和 \(y\) 使得 deep[x] <= deep[y]）。

看图：

image

  1. 对应图中的情况 \(1\) ：
    若 \(anc_{xr} = x\) 同时 \(anc_{yr} ≠ y\)，且 \(deep[anc_{xr} ] > deep[anc_{yr}] = deep[anc_{xy}]\) ，\(Lca(x, y) = x = anc_{xr}\)；
    若 \(anc_{xr} ≠ x\) 同时 \(anc_{yr} = y\)，且 \(deep[anc_{yr} ] > deep[anc_{xr}] = deep[anc_{xy}]\)，\(Lca(x, y) = x = anc_{yr}\)。

  2. 对应图中的情况 \(2\)：
    \(anc_{xr} = root\)，同时 \(anc_{yr} ≠ root\)，且 \(deep[anc_{xr} ] > deep[anc_{yr}] = deep[anc_{xy}]\)，\(Lca(x, y) = root = anc_{xr}\)；
    \(anc_{xr} ≠ root\)，同时 \(anc_{yr} = root\)，且 \(deep[anc_{yr} ] > deep[anc_{xr}] = deep[anc_{xy}]\)，\(Lca(x, y) = root = anc_{yr}\)；
    \(anc_{xr} = root\)，同时 \(anc_{yr} = root\)，且 \(deep[anc_{xr} ] = deep[anc_{yr}] = deep[anc_{xy}]\)，\(Lca(x, y) = root = anc_{xr} = anc_{yr} = anc_{xy}\)。

  3. 对应图中的情况 \(3\)：
    \(anc_{xr} ≠ root ≠ x，anc_{yr} ≠ root ≠ y\)，\(Lca(x, y) = anc_{xy}\)。

  4. 对应图中的情况 \(4\)：
    \(anc_{xr} ≠ root ≠ x，anc_{yr} ≠ root ≠ y\)，\(deep[anc_{yr}] > deep[anc_{xr}] = deep[anc_{xy}]\)，\(Lca(x, y) = anc_{yr}\)。

然后，我们可以得到一个性质：\(Lca(x,y)\) 是 \(anc_{xy}，anc_{xr}，anc_{yr}\) 三者中的深度最大值。

再得出了 \(Lca(x, y)\) 之后，我们再像上道例题的查询一样分类讨论来修改 \(Lca(x,y)\) 的子树即可。

Code

#include<cstdio>
#include<algorithm>

#define LL long long

using namespace std;

const int MAXN = 1e5 + 10;
int n, q, cnt, num, root;
int head[MAXN], dis[MAXN], val[MAXN];
int fa[MAXN], son[MAXN], size[MAXN], deep[MAXN];
int dfn[MAXN], top[MAXN];

struct Edge{
    int to, next;
}e[MAXN << 1];

inline void Add(int u, int v){
    e[++cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

void dfs_deep(int rt, int father, int depth){
    size[rt] = 1;
    fa[rt] = father;
    deep[rt] = depth;

    int max_son = -1;
    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(v == father) continue;

        dfs_deep(v, rt, depth + 1);
        size[rt] += size[v];

        if(max_son < size[v]){
            son[rt] = v;
            max_son = size[v];
        }
    }
}

void dfs_top(int rt, int top_fa){
    dfn[rt] = ++num;
    top[rt] = top_fa;
    val[num] = dis[rt];

    if(!son[rt]) return;
    dfs_top(son[rt], top_fa);

    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(!dfn[v]) dfs_top(v, v);
    }
}

struct Segment_Tree{
    struct Tree{
        int l, r;
        LL sum;
        LL lazy;
    }tr[MAXN << 2];

    inline int lson(int rt){
        return rt << 1;
    }

    inline int rson(int rt){
        return rt << 1 | 1;
    }

    inline void Pushup(int rt){
        tr[rt].sum = tr[lson(rt)].sum + tr[rson(rt)].sum;
    }

    inline void Pushdown(int rt){
        if(tr[rt].lazy){
            tr[lson(rt)].lazy += tr[rt].lazy;
            tr[rson(rt)].lazy += tr[rt].lazy;
            tr[lson(rt)].sum += 1LL * (tr[lson(rt)].r - tr[lson(rt)].l + 1) * tr[rt].lazy;
            tr[rson(rt)].sum += 1LL * (tr[rson(rt)].r - tr[rson(rt)].l + 1) * tr[rt].lazy;
            tr[rt].lazy = 0;
        }
    }

    void Build(int rt, int l, int r){
        tr[rt].l = l;
        tr[rt].r = r;

        if(l == r){
            tr[rt].sum = val[l];
            return;
        }

        int mid = (l + r) >> 1;
        Build(lson(rt), l, mid);
        Build(rson(rt), mid + 1, r);

        Pushup(rt);
    }

    void Update(int rt, int l, int r, int data){
        if(tr[rt].l >= l && tr[rt].r <= r){
            tr[rt].lazy += data;
            tr[rt].sum += 1LL * (tr[rt].r - tr[rt].l + 1) * data;
            return;
        }

        Pushdown(rt);

        int mid = (tr[rt].l + tr[rt].r) >> 1;
        if(l <= mid) Update(lson(rt), l, r, data);
        if(r > mid) Update(rson(rt), l, r, data);

        Pushup(rt);
    }

    LL Query_Sum(int rt, int l, int r){
        if(tr[rt].l >= l && tr[rt].r <= r)
            return tr[rt].sum;
        
        Pushdown(rt);

        LL ans = 0;
        int mid = (tr[rt].l + tr[rt].r) >> 1;
        if(l <= mid) ans += Query_Sum(lson(rt), l, r);
        if(r > mid) ans += Query_Sum(rson(rt), l, r);

        return ans;
    }
}S;

int Get_Lca(int x, int y){
    while(top[x] != top[y]){
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }

    if(deep[x] > deep[y]) swap(x, y);

    return x;
}

int LCA(int x, int y){
    int anc_xr = Get_Lca(x, root), anc_yr = Get_Lca(y, root), anc_xy = Get_Lca(x, y);
    if(deep[anc_xy] < deep[anc_xr]) swap(anc_xy, anc_xr);
    if(deep[anc_xy] < deep[anc_yr]) swap(anc_xy, anc_yr);

    return anc_xy;
}

int Get_Son(int x, int y){
    while(top[x] != top[y]){
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        if(fa[top[x]] == y) return top[x];
        x = fa[top[x]];
    }

    if(deep[x] > deep[y]) swap(x, y);
    return son[x];
}

int main(){
    n = read(), q = read();
    for(register int i = 1; i <= n; i++)
        dis[i] = read();
    for(register int i = 1; i <= n - 1; i++){
        int u, v;
        u = read(), v = read();
        Add(u, v);
        Add(v, u);
    }

    root = 1;
    dfs_deep(1, 0, 1);
    dfs_top(1, 1);
    S.Build(1, 1, n);

    for(register int i = 1; i <= q; i++){
        int opt;
        opt = read();

        if(opt == 1) root = read();
        else if(opt == 2){
            int u, v, x, anc;
            u = read(), v = read(), x = read();
            anc = LCA(u, v);

            if(anc == root) S.Update(1, 1, n, x);
            else if(dfn[root] < dfn[anc] || dfn[root] > dfn[anc] + size[anc] - 1)
                S.Update(1, dfn[anc], dfn[anc] + size[anc] - 1, x);
            else{
                int ch = Get_Son(anc, root);

                if(dfn[ch] + size[ch] - 1 == n)
                    S.Update(1, 1, dfn[ch] - 1, x);
                else{
                    S.Update(1, 1, dfn[ch] - 1, x);
                    S.Update(1, dfn[ch] + size[ch], n, x);
                }
            }
        }
        else{
            int v;
            v = read();

            if(v == root) printf("%lld\n", S.tr[1].sum);
            else if(dfn[root] < dfn[v] || dfn[root] > dfn[v] + size[v] - 1)
                printf("%lld\n", S.Query_Sum(1, dfn[v], dfn[v] + size[v] - 1));
            else{
                int ch = Get_Son(v, root);

                if(dfn[ch] + size[ch] - 1 == n)
                    printf("%lld\n", S.Query_Sum(1, 1, dfn[ch] - 1));
                else printf("%lld\n", S.Query_Sum(1, 1, dfn[ch] - 1) + S.Query_Sum(1, dfn[ch] + size[ch], n));
            }
        }
    }

    return 0;   
}

\(\mathfrak{To}\) \(\mathfrak{Be}\) \(\mathfrak{Continue}\)

posted @ 2022-09-17 19:34  TSTYFST  阅读(207)  评论(2)  编辑  收藏  举报