【学习笔记】树链剖分系列一 ——重链剖分——我是不是应该写一篇重链剖分呢

先咕着，等到哪天没有模拟赛再写。
不咕了，今天题改完的早，晚上可以填坑了。

概述

树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链。 ——百度百科

其实是用把一棵树拆分成一条条的链，再通过链来维护树的一种数据结构。

这里只讲重链剖分。

思想

把一棵树拆成若干个不相交的链，然后用一些数据结构去维护这些链。

那怎么把树拆成链？

首先，明确一些定义：

重儿子：对于每一个非叶子节点，它的儿子中，子树最大的儿子，为该节点的重儿子。

轻儿子：对于每一个非叶子节点，它的儿子中，除重儿子外的所有儿子即为轻儿子。

重边：连接任意两个重儿子的边叫做重边。

轻边：除重边以外的所有边。

重链：相邻重边连起来的，一条连接重儿子的链叫重链。

轻链：相邻轻边连起来的，一条连接轻儿子的链叫轻链。

干嚼文字定义大概率是不能明白的，为了更易理解，还是上图吧。

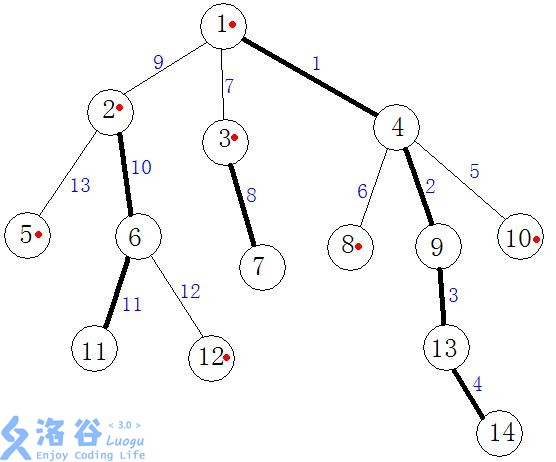
image

图中，加黑的边都是重边，它连接起来的节点都是重节点（重儿子），其余都是轻节点（轻儿子）。

边 1−2−3−4 连起来的这条链就是重链。
边 9−13 连起来的链就是轻链。

有红点标记的就是该节点所在重链的起点，称为 top 节点。

每条边上的编号其实就是 dfs 进行的顺序，即 dfs 序。

接我们上边的问题，怎么把它拆成链？

仔细观察上图，可以发现找出每个节点的重儿子，这棵树就自然而然的被拆成了若干重链和轻链。

所以，进行一遍 dfs 就可找出每个节点的重儿子。

void dfs_deep(int rt, int father, int depth){
    size[rt] = 1; //以rt为根的子树的大小 
    fa[rt] = father; //rt的父亲
    deep[rt] = depth; //rt的深度 
 
    int max_son = -1; //最大的儿子的子树大小 
    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(v == father) continue;
 
        dfs_deep(v, rt, depth + 1);
        size[rt] += size[v];
 
        if(size[v] > max_son){
            son[rt] = v; //重儿子 
            max_son = size[v];
        }
    }
}

问题又来了，怎么去维护这些链？

如果认真观察过上图后，我们可以发现重链的编号是连续的。

因此我们需要对整棵树进行重新编号，然后利用 dfs 序的思想用线段树维护。

因此，再进行一遍 dfs 来重新编号，注意在编号的时候要先访问重儿子，这样才能保证重链内的节点编号连续。

void dfs_top(int rt, int top_fa){
    dfn[rt] = ++num; //dfs序
    top[rt] = top_fa; //rt所在的重链的起点 
 
    if(!son[rt]) return; //没有重儿子，是叶子节点，直接退出
    dfs_top(son[rt], top_fa); //先访问重儿子 
 
    for(register int i = head[rt]; i; i = e[i].next){
        int v = e[i].to;
        if(!dfn[v]) dfs_top(v, v); //如果其他轻儿子没有访问过，肯定在另一条链，并且是起点 
    }
}

之后就可以在线段树上转化成区间去搞了。

有一个显然的性质：
以 i 为根的子树的树在线段树上的编号为 [i,i+子树节点数−1]。

接下来结合例题来看：

P3384 【模板】轻重链剖分/树链剖分

树链剖分都挂在脸上了喂。

dfs 已在上文讲述，这里不在赘述。

从把根据重新编完号的树映射到线段树上开始。

struct Segment_Tree{
	struct Tree{
		int l, r;
		int sum;
		int lazy;
	}tr[MAXN << 2];
	
	inline int lson(int rt){
		return rt << 1;
	}
	
	inline int rson(int rt){
		return rt << 1 | 1;
	}
	
	void Pushup(int rt){
		tr[rt].sum = (tr[lson(rt)].sum + tr[rson(rt)].sum) % p;
	}
	
	void Pushdown(int rt){
		if(tr[rt].lazy){
			tr[lson(rt)].lazy = (tr[lson(rt)].lazy + tr[rt].lazy) % p;
			tr[rson(rt)].lazy = (tr[rson(rt)].lazy + tr[rt].lazy) % p;
			tr[lson(rt)].sum = (tr[lson(rt)].sum + (tr[lson(rt)].r - tr[lson(rt)].l + 1) * tr[rt].lazy) % p;
			tr[rson(rt)].sum = (tr[rson(rt)].sum + (tr[rson(rt)].r - tr[rson(rt)].l + 1) * tr[rt].lazy) % p;
			tr[rt].lazy = 0;
		}
	}
	
	void Build(int rt, int l, int r){
		tr[rt].l = l;
		tr[rt].r = r;
		
		if(l == r){
			tr[rt].sum = val[l] % p;
			return;
		}
		
		int mid = (l + r) >> 1;
		Build(lson(rt), l, mid);
		Build(rson(rt), mid + 1, r);
		
		Pushup(rt);
	}
	
	void Update(int rt, int l, int r, int data){
		if(l <= tr[rt].l && r >= tr[rt].r){
			tr[rt].sum = (tr[rt].sum + (tr[rt].r - tr[rt].l + 1) * data) % p;
			tr[rt].lazy = (tr[rt].lazy + data) % p;
			return;
		}
		
		Pushdown(rt);
		
		int mid = (tr[rt].l + tr[rt].r) >> 1;
		if(l <= mid) Update(lson(rt), l, r, data);
		if(r > mid) Update(rson(rt), l, r, data);
		
		Pushup(rt);
	}
	
	int Query_sum(int rt, int l, int r){
		if(l <= tr[rt].l && r >= tr[rt].r)
			return tr[rt].sum % p;
		
		Pushdown(rt);
		
		int mid = (tr[rt].l + tr[rt].r) >> 1;
		if(r <= mid) return Query_sum(lson(rt), l, r);
		else if(l > mid) return Query_sum(rson(rt), l, r);
		else return Query_sum(lson(rt), l, r) + Query_sum(rson(rt), l, r);
	}	
}S;

线段树基础操作应该都会吧，不会的话建议先去学线段树。不会线段树应该也不会看到这吧。

考虑如何实现树上的操作。

树链剖分的思想是：对于两个不在同一重链内的节点,让他们不断地跳,使得他们处于同一重链上。

是不是有点像倍增LCA。

那怎么跳？

回想起第一次 dfs 记录的 deep 数组，第二次 dfs 记录的 top 数组。

设两个节点 x，y。

每次让 deep[top[x]] 与 deep[top[y]] 大的在下边，然后让它往上跳。

例如 deep[top[x]]>deep[top[y]] 时，让 x 节点跳到 top[x]，之后在线段树上更新 x 经过的链。

跳到最后 x，y 肯定就在同一条重链上了，而重链上的节点是连续的，直接在线段树上进行操作即可。

void Update_Tree(int x, int y, int data){
	while(top[x] != top[y]){
		if(deep[top[x]] < deep[top[y]]) swap(x, y);
		S.Update(1, dfn[top[x]], dfn[x], data);
		x = fa[top[x]];
	}
	
	if(deep[x] > deep[y]) swap(x, y);
	S.Update(1, dfn[x], dfn[y], data);
}

查询操作同理，在向上跳的过程中对每条链上点的权值的和加和，最后对线段树查询一次即可。

int Query_sum_Tree(int x, int y){
	int ans = 0;
	
	while(top[x] != top[y]){
		if(deep[top[x]] < deep[top[y]]) swap(x, y);
		ans += S.Query_sum(1, dfn[top[x]], dfn[x]);
		x = fa[top[x]];
	}
	
	if(deep[x] > deep[y]) swap(x, y);
	ans = (ans + S.Query_sum(1, dfn[x], dfn[y])) % p;
	
	return ans;
}

至于有关子树的操作，我们已经把一颗树拍扁成了一个序列，所以用线段树即可直接维护。

结合上边说的那条显然的性质（以 i 为根的子树的树在线段树上的编号为 [i,i+子树节点数−1]）和我们维护的 size 数组，

对子树的修改：

S.Update(1, dfn[x], dfn[x] + size[x] - 1, data);

查询：

S.Query_sum(1, dfn[x], dfn[x] + size[x] - 1)

Code

#include<cstdio>
#include<cstdlib>
#include<algorithm>
 
using namespace std;
 
const int MAXN = 1e5 + 10;
int n, m, root, p, cnt, num;
int dis[MAXN], head[MAXN];
int deep[MAXN], fa[MAXN], son[MAXN], size[MAXN];
int dfn[MAXN], val[MAXN], top[MAXN];
 
struct Edge{
	int to, next;
}e[MAXN << 1];
 
inline void Add(int u, int v){
	e[++cnt].to = v;
	e[cnt].next = head[u];
	head[u] = cnt;
}
 
void dfs_deep(int rt, int father, int depth){
	size[rt] = 1;
	fa[rt] = father;
	deep[rt] = depth;
	
	int max_son = -1;
	for(register int i = head[rt]; i; i = e[i].next){
		int v = e[i].to;
		if(v == father) continue;
		
		dfs_deep(v, rt, depth + 1);
		
		size[rt] += size[v];
		if(size[v] > max_son){
			son[rt] = v;
			max_son = size[v];
		}
	}
}
 
void dfs_top(int rt, int top_fa){
	dfn[rt] = ++num;
	top[rt] = top_fa;
	val[num] = dis[rt];
	
	if(!son[rt]) return;
	
	dfs_top(son[rt], top_fa);
	
	for(register int i = head[rt]; i; i = e[i].next){
		int v = e[i].to;
		if(!dfn[v]) dfs_top(v, v);
	}
}
 
struct Segment_Tree{
	struct Tree{
		int l, r;
		int sum;
		int lazy;
	}tr[MAXN << 2];
	
	inline int lson(int rt){
		return rt << 1;
	}
	
	inline int rson(int rt){
		return rt << 1 | 1;
	}
	
	void Pushup(int rt){
		tr[rt].sum = (tr[lson(rt)].sum + tr[rson(rt)].sum) % p;
	}
	
	void Pushdown(int rt){
		if(tr[rt].lazy){
			tr[lson(rt)].lazy = (tr[lson(rt)].lazy + tr[rt].lazy) % p;
			tr[rson(rt)].lazy = (tr[rson(rt)].lazy + tr[rt].lazy) % p;
			tr[lson(rt)].sum = (tr[lson(rt)].sum + (tr[lson(rt)].r - tr[lson(rt)].l + 1) * tr[rt].lazy) % p;
			tr[rson(rt)].sum = (tr[rson(rt)].sum + (tr[rson(rt)].r - tr[rson(rt)].l + 1) * tr[rt].lazy) % p;
			tr[rt].lazy = 0;
		}
	}
	
	void Build(int rt, int l, int r){
		tr[rt].l = l;
		tr[rt].r = r;
		
		if(l == r){
			tr[rt].sum = val[l] % p;
			return;
		}
		
		int mid = (l + r) >> 1;
		Build(lson(rt), l, mid);
		Build(rson(rt), mid + 1, r);
		
		Pushup(rt);
	}
	
	void Update(int rt, int l, int r, int data){
		if(l <= tr[rt].l && r >= tr[rt].r){
			tr[rt].sum = (tr[rt].sum + (tr[rt].r - tr[rt].l + 1) * data) % p;
			tr[rt].lazy = (tr[rt].lazy + data) % p;
			return;
		}
		
		Pushdown(rt);
		
		int mid = (tr[rt].l + tr[rt].r) >> 1;
		if(l <= mid) Update(lson(rt), l, r, data);
		if(r > mid) Update(rson(rt), l, r, data);
		
		Pushup(rt);
	}
	
	int Query_sum(int rt, int l, int r){
		if(l <= tr[rt].l && r >= tr[rt].r)
			return tr[rt].sum % p;
		
		Pushdown(rt);
		
		int mid = (tr[rt].l + tr[rt].r) >> 1;
		if(r <= mid) return Query_sum(lson(rt), l, r);
		else if(l > mid) return Query_sum(rson(rt), l, r);
		else return Query_sum(lson(rt), l, r) + Query_sum(rson(rt), l, r);
	}	
}S;
 
int Query_sum_Tree(int x, int y){
	int ans = 0;
	
	while(top[x] != top[y]){
		if(deep[top[x]] < deep[top[y]]) swap(x, y);
		ans += S.Query_sum(1, dfn[top[x]], dfn[x]);
		x = fa[top[x]];
	}
	
	if(deep[x] > deep[y]) swap(x, y);
	ans = (ans + S.Query_sum(1, dfn[x], dfn[y])) % p;
	
	return ans;
}
 
void Update_Tree(int x, int y, int data){
	while(top[x] != top[y]){
		if(deep[top[x]] < deep[top[y]]) swap(x, y);
		S.Update(1, dfn[top[x]], dfn[x], data);
		x = fa[top[x]];
	}
	
	if(deep[x] > deep[y]) swap(x, y);
	S.Update(1, dfn[x], dfn[y], data);
}
 
inline int read(){
	int x = 0, f = 1;
	char c = getchar();
	
	while(c < '0' || c > '9'){
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	
	return x * f;
}
 
int main(){
	n = read(), m = read(), root = read(), p = read();
	for(register int i = 1; i <= n; i++) dis[i] = read();
	for(register int i = 1; i <= n - 1; i++){
		int u, v;
		u = read(), v = read();
		Add(u, v);
		Add(v, u);
	}
	
	dfs1(root, 0, 1);
	dfs2(root, root);
	S.Build(1, 1, n);
	
	for(register int i = 1; i <= m; i++){
		int opt;
		opt = read();
		
		if(opt == 1){
			int x, y, data;
			x = read(), y = read(), data = read();
			Update_Tree(x, y, data);
		}
		else if(opt == 2){
			int x, y;
			x = read(), y = read();
			printf("%d\n", Query_sum_Tree(x, y) % p);
		}
		else if(opt == 3){
			int x, data;
			x = read(), data = read();
			S.Update(1, dfn[x], dfn[x] + size[x] - 1, data);
		}
		else if(opt == 4){
			int x;
			x = read();
			printf("%d\n", S.Query_sum(1, dfn[x], dfn[x] + size[x] - 1) % p);
		}
	}
	
	return 0;
}

模板题

P3384 【模板】轻重链剖分/树链剖分

P2146 [NOI2015] 软件包管理器

P2590 [ZJOI2008]树的统计

P3833 [SHOI2012]魔法树

P3178 [HAOI2015]树上操作

CF343D Water Tree

P4116 Qtree3

求LCA

续集1：【学习笔记】树链剖分系列二——LCA

P4281 [AHOI2008]紧急集合 / 聚会

P1967 [NOIP2013 提高组] 货车运输

P4427 [BJOI2018]求和

点权转边权

续集2 ：【学习笔记】树链剖分系列三——点权转边权

P4315 月下“毛景树”

P4114 Qtree1

P3038 [USACO11DEC]Grass Planting G

CF165D Beard Graph

P3950 部落冲突

换根操作

续集3：【学习笔记】树链剖分系列四——换根操作

CF916E Jamie and Tree

P3979 遥远的国度

带思维含量的

P1505 [国家集训队]旅游

P2486 [SDOI2011]染色

P3313 [SDOI2014]旅行

P4092 [HEOI2016/TJOI2016]树

P7735 [NOI2021] 轻重边

posted @   TSTYFST  阅读(89)  评论(1)  编辑  收藏  举报
相关博文：
· 【学习笔记】树链剖分系列四——换根操作
· 【学习笔记】树链剖分系列三——边权转点权
· 树链剖分 笔记与题集
· 「学习笔记」树链剖分
· 浅谈树链剖分—轻重链剖分
阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 开源Multi-agent AI智能体框架aevatar.ai，欢迎大家贡献代码
· Manus重磅发布：全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· AI技术革命，工作效率10个最佳AI工具
点击右上角即可分享
微信分享提示
AI IDE Trae