【学习笔记/模板】扫描线 周长并

周长并

絮絮叨叨，切切喳喳

上午摆，发现自己还有个周长并的坑，打算填，然后一干就一个上午。然而别人一上午五道紫题，人与人的体制不能一概而论了属于是。

晚上先去摆了NOI的笔试模拟，然后就楼了几眼 €€£ 的笔试题库，然后居然神奇的记住了大部分出的题，可能天赋点都点在没啥用（至少对OI用处不大）的地方了。加上今天 rp 爆发rp 都用这上边了，可不你模拟赛场场爆炸呢，不会的还都蒙对了，于是乎可能是唯一一次AK + Rank 1，泵。

例题

P1856 [IOI1998] [USACO5.5] 矩形周长Picture

思想

学周长并的人大抵都学过面积并了罢。
学过面积并肯定对扫描线的思想至少是了解的罢。

和面积并一样，有几个矩形：（图片来自网络）

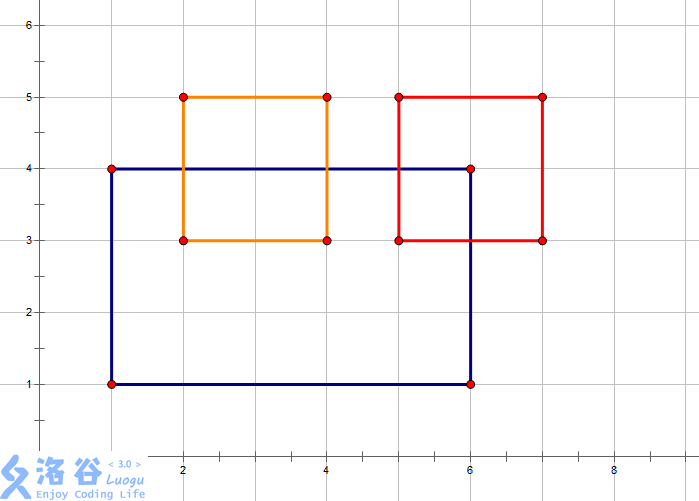
想象有一条线，从下到上扫描完整个图案，遇到每条上边或下边就停下：

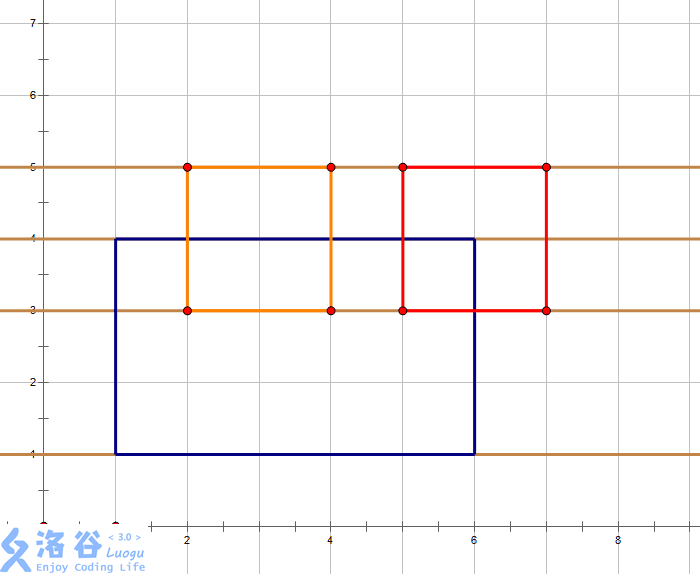
每次停下后再对区间进行处理。

因为是周长，所以还有一条从左扫到右的线。

最后的加和就是周长。

实现

不同于其他大佬令人拍手叫绝的扫一遍操作，本蒟蒻使用的是更好理解的上下，左右各扫一遍。

所以，需要把矩形拆成上下，左右两组边，再用两棵线段树维护。

矩形的边设立一个结构体存储：

struct Line{
    int s;  //维护线段端点的另一个值
    int l, r; //维护线段端点的 x / y 值
    int sit;
}line_x[MAXN << 1]/*横边*/, line_y[MAXN << 1]/*竖边*/;

为了扫描，要对横边按照 \(y\) 值升序排序，对竖边按照 \(x\) 值升序排序。

需要注意的是，当两个矩形的边重合时，横/竖边的 \(y/x\) 值相同，这就需要我们让入边在前。
如果不这样的话会多算一遍出边。所以，cmp函数：

inline bool cmp(const Line &a, const Line &b){
    if(a.s == b.s) //如果相同，入边在前 
        return a.sit > b.sit;
    return a.s < b.s; //升序排序
}

然后是答案统计，一条边对周长的贡献，在于它对线段树产生的影响，就像人生的意义在于奉献一样。

其实就是和线段树上次存的边相减，取个绝对值。
自己画画图就能出来，才不是因为今天累了，懒得详细写了（英梨梨嘴脸）。

所以，这就没什么了，想清楚还是很好写的。

剩下的维护线段树就和面积并一样了，完结撒花。

Code

#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1e5 + 10;
int n, tot_x, tot_y, last_x, last_y;
long long sum;
int val_x[MAXN], val_y[MAXN]; //存离散化前的值 
int x[MAXN], y[MAXN]; //离散化用临时数组

struct Line{
    int s;  //维护线段端点的另一个值
    int l, r; //维护线段端点的 x / y 值
    int sit;
}line_x[MAXN << 1]/*横边*/, line_y[MAXN << 1]/*竖边*/;

inline bool cmp(const Line &a, const Line &b){
    if(a.s == b.s) //如果相同，入边在前 
        return a.sit > b.sit;
    return a.s < b.s; //升序排序
}

struct Segment_Tree{
    struct Tree{
        int l, r;
        int len; //区间的线段的长度 
        int cnt; //有几条覆盖整个区间的线段  
    }tr[MAXN << 2];

    inline int lson(int rt){
        return rt << 1;
    }

    inline int rson(int rt){
        return rt << 1 | 1;
    }

    inline void Pushup(int rt, int *val){
        if(tr[rt].cnt) //如果被整体覆盖了 
            tr[rt].len = val[tr[rt].r + 1] - val[tr[rt].l]; //就是右端点减去左端点 
        else //没被整体覆盖
            tr[rt].len = tr[lson(rt)].len + tr[rson(rt)].len; //从儿子身上往上捯 
    }

    void Build(int rt, int l, int r){
        tr[rt].l = l;
        tr[rt].r = r;
        tr[rt].len = 0;
        tr[rt].cnt = 0;

        if(l == r) //叶子节点为空，没有意义 
            return;

        int mid = (l + r) >> 1;
        Build(lson(rt), l, mid);
        Build(rson(rt), mid + 1, r);
    }

    void Update(int rt, int l, int r, int data, int *val){
        if(tr[rt].l >= l && tr[rt].r <= r){ //整体覆盖 
            tr[rt].cnt += data; //其实和懒标记差不多 
            Pushup(rt, val);

            return;
        }

        int mid = (tr[rt].l + tr[rt].r) >> 1;
        if(l <= mid) Update(lson(rt), l, r, data, val);
        if(r > mid) Update(rson(rt), l, r, data, val);

        Pushup(rt, val);
    }
}S_x/*从下往上扫*/, S_y/*从左往右扫*/;

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

int main(){
    n = read();
    for(register int i = 1; i <= n; i++){
        int x1, y1, x2, y2;
        x1 = read(), y1 = read(), x2 = read(), y2 = read();

        //line_x存横边 
        line_x[(i << 1) - 1].s = y1, line_x[(i << 1)].s = y2;
        line_x[(i << 1) - 1].l = line_x[(i << 1)].l = x1;
        line_x[(i << 1) - 1].r = line_x[(i << 1)].r = x2;
        line_x[(i << 1) - 1].sit = 1; 
        line_x[(i << 1)].sit = -1; 
        x[++tot_x] = x1;
        x[++tot_x] = x2;
        //line_y存竖边
        line_y[(i << 1) - 1].s = x1, line_y[(i << 1)].s = x2;
        line_y[(i << 1) - 1].l = line_y[(i << 1)].l = y1;
        line_y[(i << 1) - 1].r = line_y[(i << 1)].r = y2;
        line_y[(i << 1) - 1].sit = 1; 
        line_y[(i << 1)].sit = -1;
        y[++tot_y] = y1;
        y[++tot_y] = y2;
    }

    n <<= 1; 
    sort(x + 1, x + 1 + tot_x);
    sort(y + 1, y + 1 + tot_y);
    int cnt_x = unique(x + 1, x + 1 + tot_x) - x - 1;
    int cnt_y = unique(y + 1, y + 1 + tot_y) - y - 1;
    for(register int i = 1; i <= n; i++){
        int pos_x1 = lower_bound(x + 1, x + 1 + cnt_x, line_x[i].l) - x;
        int pos_x2 = lower_bound(x + 1, x + 1 + cnt_x, line_x[i].r) - x;
        int pos_y1 = lower_bound(y + 1, y + 1 + cnt_y, line_y[i].l) - y;
        int pos_y2 = lower_bound(y + 1, y + 1 + cnt_y, line_y[i].r) - y;

        val_x[pos_x1] = line_x[i].l;
        val_x[pos_x2] = line_x[i].r;
        line_x[i].l = pos_x1;
        line_x[i].r = pos_x2;

        val_y[pos_y1] = line_y[i].l;
        val_y[pos_y2] = line_y[i].r;
        line_y[i].l = pos_y1;
        line_y[i].r = pos_y2;
    } //离散化基础操作 

    sort(line_x + 1, line_x + 1 + n, cmp);
    sort(line_y + 1, line_y + 1 + n, cmp);
    S_x.Build(1, 1, n);
    S_y.Build(1, 1, n);

    for(register int i = 1; i <= n; i++){
        S_x.Update(1, line_x[i].l, line_x[i].r - 1, line_x[i].sit, val_x); //更新横边 
        S_y.Update(1, line_y[i].l, line_y[i].r - 1, line_y[i].sit, val_y); //更新竖边 
        sum += abs(S_x.tr[1].len - last_x) + abs(S_y.tr[1].len - last_y); //统计答案 
        last_x = S_x.tr[1].len; //记录上次线段树的值 
        last_y = S_y.tr[1].len;
    }

    printf("%lld\n", sum);

    return 0;
}