计算几何和哈希能组合出什么？OIer竟惊叹连连！Luogu P3454 [POI2007]OSI-Axes of Symmetry 题解

[POI2007]OSI-Axes of Symmetry

题目

链接：P3454 [POI2007]OSI-Axes of Symmetry

大意：

给定 \(n\) 个点，点全部按顺时针或逆时针的顺序给出。求这 \(n\) 个点围成的多边型的对称轴的数量。

思路：

点既然按顺序给出，就可以依次记录多边形的角和边，连在一起就得到了一个长为 \(2n\) 的环，最后一项连接着第一项。

我们把样例那个六边形拿出来：

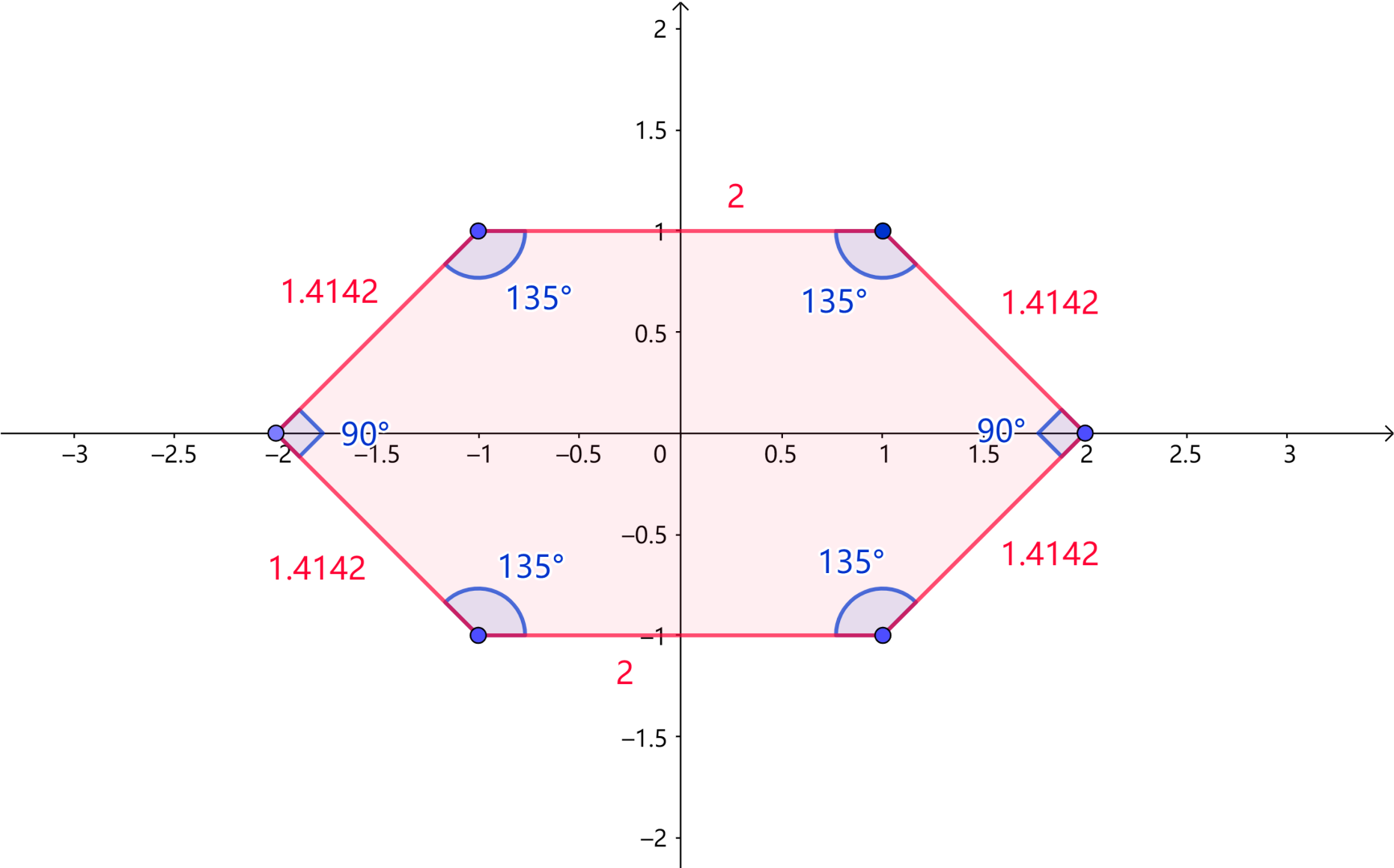
角度是实数，不太好维护，所以可以用计算几何的一个小方法，叉积。

众所周知，\(\vec{a}\times\vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot sin<\vec{a}, \vec{b}>\) 。所以叉积可以代替角。

同样的，边长可以用它的平方代替，免去开方。

这样，一个实数环就可以转化成整数环。
上图，环就可以变成：

\[2 → 2 → 2 → 2 → 4 → 2 → 2 → 2 → 2 → 2 → 4 → 2 \]

于是乎，一个看似是计算几何的问题就可以转化为：环上有几个位置，满足将环从这里断开后，可以得到一条回文链。

同时，一条对称轴穿过两个位置，最后的答案就是满足的位置的个数除以二。

so，这就结束了吗？

我们来看这样一组数据：

input:
1
4
0 0
1 1
2 1
1 0

output:
0

对应的图：

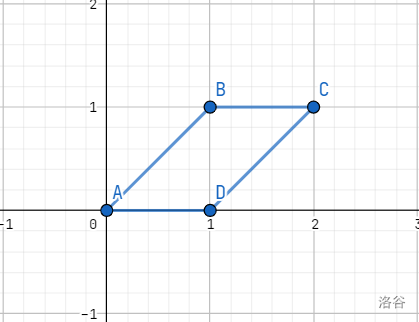
如果我们只用 \(\vec{a}\times\vec{b}\) 来判断角会错，这里 \(∠BAD = \frac{\pi }{4}\) ，\(∠ABC = \frac{3\pi }{4}\) ，然而 \(sin \frac{\pi }{4} = sin \frac{3\pi }{4}\) ，所以，序列会变成：

\[2 → 1 → 1 → 1 → 2 → 1 → 1 → 1 → 2 \]

所以，会错误的判断出有四个位置，两条对称轴。

既然锅出在角上，能不能再维护一个序列？

叉积依靠 \(sin\) 值表示角，那我们可以再维护一个 \(cos\) 值。
显然，我们可以想到点积，
\(\vec{a}\cdot\vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot cos<\vec{a}, \vec{b}>\) 。

再利用点积维护一个序列，hack数据的点积序列为：

\[2 → -1 → 1 → 1 → 2 → -1 → 1 → 1 \]

样例六边形的点积序列为：

\[2 → 0 → 2 → -2 → 4 → -2 → 2 → 0 → 2 → -2 → 4 → -2 \]

同上边的叉积序列比较，不难得出，当一个位置能同时把叉积序列和点积序列都断成回文串时，这个位置才满足要求。

之后就是处理环了，常见的方法是破环为链，然后把序列复制一份到后面。

对于每个 \(1 \leq i \leq 2n\) ，检查区间 \(\left [ i ,i + 2n\right ]\) 是否是回文串（断环成链），此处用哈希求解。

Code:

#include<cstdio>
#include<algorithm>

#define ULL unsigned long long

using namespace std;

const int MAXN = 100010;
const int Base = 233;
int t, n, ans;
long long s1[MAXN << 2]/*叉乘序列*/, s2[MAXN << 2]/*点乘序列*/;
ULL power[MAXN << 2], hash_l_1[MAXN << 2], hash_r_1[MAXN << 2];
ULL hash_l_2[MAXN << 2], hash_r_2[MAXN << 2];

struct Dikayer{
    int x, y;
}p[MAXN];

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
} 

long long Get_Cross(Dikayer a, Dikayer b, Dikayer c){
    return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
} //求 ab 叉乘 ac

long long Get_Point(Dikayer a, Dikayer b, Dikayer c){
    return (b.x - a.x) * (c.x - a.x) + (b.y - a.y) * (c.y - a.y);
} //求 ab 点乘 ac

long long Get_Dis(Dikayer a, Dikayer b){
    return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
} //求 ab 的长度 

bool Check(int l, int r){ //正反的哈希值一样，即为回文串
    ULL res_l_1 = hash_l_1[r] - hash_l_1[l - 1] * power[r - l + 1];
    ULL res_r_1 = hash_r_1[l] - hash_r_1[r + 1] * power[r - l + 1];
    ULL res_l_2 = hash_l_2[r] - hash_l_2[l - 1] * power[r - l + 1];
    ULL res_r_2 = hash_r_2[l] - hash_r_2[r + 1] * power[r - l + 1];

    if(res_l_1 == res_r_1 && res_l_2 == res_r_2) return true; //叉乘序列和点乘序列都为回文串 
    else return false;
}

void init(){
    power[0] = 1;
    for(register int i = 1; i < (MAXN << 2); i++)
        power[i] = power[i - 1] * Base;
}

void Get_Hash(long long *s, ULL *hash_l, ULL *hash_r){
    for(register int i = 1; i <= (n << 2); i++)
        hash_l[i] = hash_l[i - 1] * Base + s[i];
    for(register int i = (n << 2); i >= 1; i--)
        hash_r[i] = hash_r[i + 1] * Base + s[i];
}

int main(){
    init();

    t = read();
    while(t--){
        ans = 0;
        n = read();
        for(register int i = 1; i <= n; i++)
            p[i].x = read(), p[i].y = read();
        
        for(register int i = 1; i <= n; i++){
            int pos1 = i, pos2 = i + 1, pos3 = i + 2;
            pos2 > n ? pos2 -= n : pos2 += 0;
            pos3 > n ? pos3 -= n : pos3 += 0;

            int edge = Get_Dis(p[pos1], p[pos2]); //边 
            int angle_sin = Get_Cross(p[pos2], p[pos1], p[pos3]); //角sin
            int angle_cos = Get_Point(p[pos2], p[pos1], p[pos3]);//角cos

            s1[(i << 1) - 1] = edge;
            s1[i << 1] = angle_sin;
            s2[(i << 1) - 1] = edge;
            s2[i << 1] = angle_cos;
        }

        for(register int i = 1; i <= (n << 1); i++){
            s1[i + (n << 1)] = s1[i];
            s2[i + (n << 1)] = s2[i];
        } //复制一遍 

        Get_Hash(s1, hash_l_1, hash_r_1);
        Get_Hash(s2, hash_l_2, hash_r_2);

        for(register int i = 1; i <= (n << 1); i++)
            if(Check(i, i + (n << 1))) ans++;
        
        printf("%d\n", ans / 2);
    }

    return 0;
}