【学习笔记/模板】主席树

可持久化线段树(主席树)

概述

可持久化？

可持久化数据结构总是可以保留每一个历史版本，并且支持操作的不可变特性 。

可持久化线段树？主席树？

可持久化线段树最大的特点是：可以访问历史版本 。如，我对线段树进行了1000次修改操作，突然问你第233次修改之后某个区间的区间和是多少——这个问题可持久化线段树就可以正常地回答出来。

至于主席树这个名字，好像是发明人的姓名缩写是 hjt 来着......

思想

保存每次操作时的历史版本，存好多棵线段树？ MLE在向你挥手。

so，考虑一下更优秀的方法？
对于线段树的每次操作实际上只会影响到log个结点，我们没必要在建立新版本时重新记录下这个版本的整棵树，只需要记录下这修改的log个结点，其余结点继承上个版本的就好。

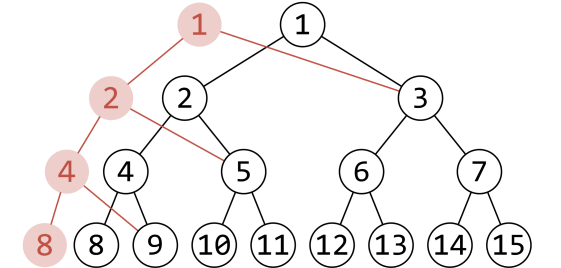
如图，标红的节点是进行了操作的节点，其他节点就可以直接继承。

当然，这样会破坏线段树原有的完全二叉树结构，所以要使用动态开点。

实现

你已经熟悉主席树了，快去自己写吧

先想象一棵普通的线段树，对它进行单点修改。被修改的是一条 \(logn\) 的链。
每次修改我们不动原节点，而是在它的旁边建一个新节点，把原来节点的信息复制到新节点上，再对新节点进行修改。

对于查询，只要记录每一次修改对应的新的根节点的编号(修改肯定要从根节点开始)，在查询时从对应的根节点向下查询即可。

代码实现

struct Chairman_Tree{
    int tot;

    struct Tree{
        int lson, rson;
        int size;
    }tr[MAXN * 25];

    Chairman_Tree(){
        tot = 0;
    }

    void Build(int &rt, int l, int r){
        rt = ++tot;

        if(l == r)
            return;
            
        int mid = (l + r) >> 1;
        Build(tr[rt].lson, l, mid);
        Build(tr[rt].rson, mid + 1, r);
    }

    void Update(int &rt, int last, int pos, int L, int R){
        rt = ++tot;
        tr[rt].lson = tr[last].lson;
        tr[rt].rson = tr[last].rson;
        tr[rt].size = tr[last].size + 1;

        if(L == R)
            return;
        
        int mid = (L + R) >> 1;
        if(pos <= mid) Update(tr[rt].lson, tr[last].lson, pos, L, mid);
        else Update(tr[rt].rson, tr[last].rson, pos, mid + 1, R);
    }

    int Query(int rt_l, int rt_r, int k, int L, int R){
        if(L == R)
            return L;

        int mid = (L + R) >> 1;
        int cut = tr[tr[rt_r].lson].size - tr[tr[rt_l].lson].size;

        if(k <= cut) return Query(tr[rt_l].lson, tr[rt_r].lson, k, L, mid);
        else return Query(tr[rt_l].rson, tr[rt_r].rson, k - cut, mid + 1, R);
    }
}C;

应用

区间第K大

例题：P3834 【模板】可持久化线段树 2

建立一颗可持久化权值线段树维护每个数出现的次数(若数范围大，需要离散化)。

从左往右扫一遍序列，在可持久化线段树中给对应的数+1。

当处理到某个询问(l, r)的右端点时，发现：对于任意一个数， 右端点加入后的线段树上的值 - 左端点加入前的线段树上的值， 就是区间中这个数出现的次数。

那么在这棵“减出来的”线段树上进行“求第k大数”查询即可。

Code

#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 2e5 + 10;
int n, m, cnt;
int a[MAXN], num[MAXN], root[MAXN];

struct Chairman_Tree{
    int tot;

    struct Tree{
        int lson, rson;
        int size;
    }tr[MAXN * 25];

    Chairman_Tree(){
        tot = 0;
    }

    void Build(int &rt, int l, int r){
        rt = ++tot;

        if(l == r)
            return;
            
        int mid = (l + r) >> 1;
        Build(tr[rt].lson, l, mid);
        Build(tr[rt].rson, mid + 1, r);
    }

    void Update(int &rt, int last, int pos, int L, int R){
        rt = ++tot;
        tr[rt].lson = tr[last].lson;
        tr[rt].rson = tr[last].rson;
        tr[rt].size = tr[last].size + 1;

        if(L == R)
            return;
        
        int mid = (L + R) >> 1;
        if(pos <= mid) Update(tr[rt].lson, tr[last].lson, pos, L, mid);
        else Update(tr[rt].rson, tr[last].rson, pos, mid + 1, R);
    }

    int Query(int rt_l, int rt_r, int k, int L, int R){
        if(L == R)
            return L;

        int mid = (L + R) >> 1;
        int cut = tr[tr[rt_r].lson].size - tr[tr[rt_l].lson].size;

        if(k <= cut) return Query(tr[rt_l].lson, tr[rt_r].lson, k, L, mid);
        else return Query(tr[rt_l].rson, tr[rt_r].rson, k - cut, mid + 1, R);
    }
}C;

inline int read(){
    int x = 0, f = 1;
    char c = getchar();

    while(c < '0' || c > '9'){
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }

    return x * f;
}

int main(){
    n = read(), m = read();
    for(register int i = 1; i <= n; i++){
        a[i] = read();
        num[i] = a[i];
    }
    
    sort(num + 1, num + 1 + n);
    cnt = unique(num + 1, num + 1 + n) - num - 1;
    C.Build(root[0], 1, cnt);
    for(register int i = 1; i <= n; i++){
        int pos = lower_bound(num + 1, num + 1 + cnt, a[i]) - num;
        C.Update(root[i], root[i - 1], pos, 1, cnt);
    }

    for(register int i = 1; i <= m; i++){
        int l, r, k;
        l = read(), r = read(), k = read();

        int ans = C.Query(root[l - 1], root[r], k, 1, cnt);
        printf("%d\n", num[ans]);
    }

    return 0;
}

题

P3919 【模板】可持久化线段树 1（可持久化数组）

P3834 【模板】可持久化线段树 2

P2468 [SDOI2010]粟粟的书架