【学习笔记】二维凸包

只会二维凸包，其他的都不会

概述

凸包是啥

凸包（Convex Hull）是一个计算几何（图形学）中的概念。
在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造。
在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。
用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。——摘自《百度百科》

当然，这不重要，凸包一般长这样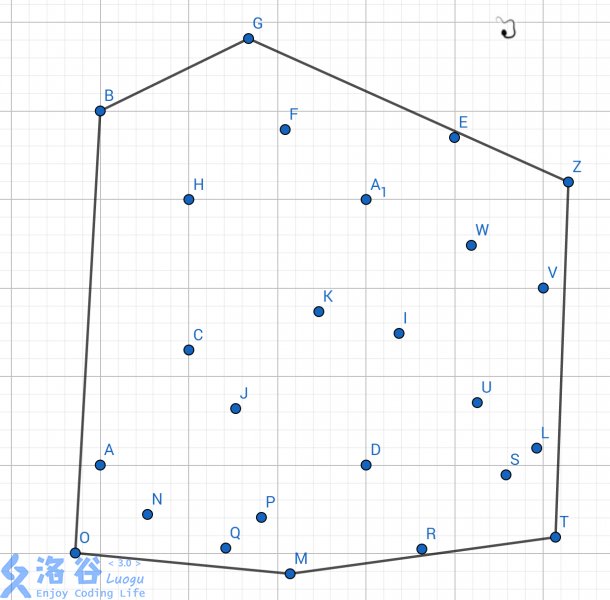：$$图1.1$$

凸包在OI中的应用远超计算几何的范畴，除了一些对求凸包的显性考察外，用数据结构维护动态凸包，斜率优化等中都有所涉及。

然而，这里只会讲放凸包的计算几何算法

例题

P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包

算法实现

Graham扫描法

首先找到最靠近左下的那个点，这个点一定在凸包上，不然就不是把最外层围起来了。
其中，左下强调下，即以 \(y\) 轴为第一关键字。

\[图2.1 \]

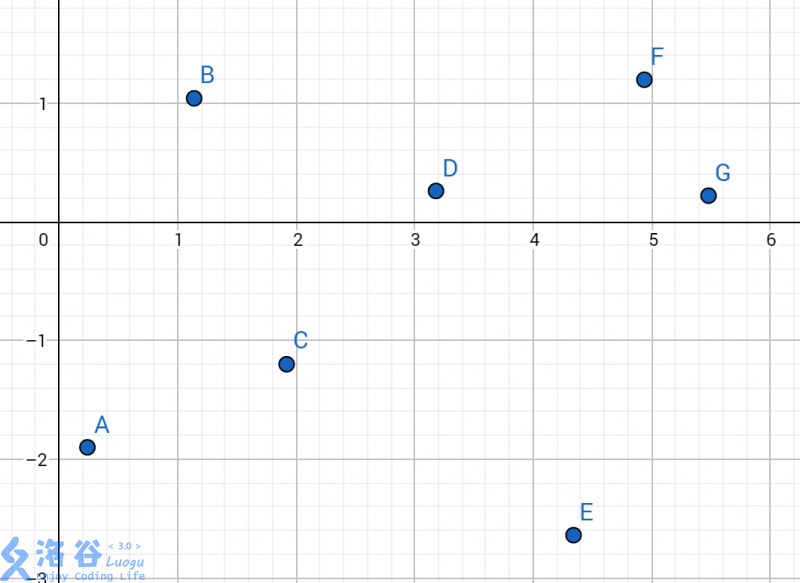
如上图，最靠近左下的是点E，而不是点A。

---

然后，以这个点为极点，其他点按照极角排序。

这里先介绍一个黑科技：\(atan2\) 函数
atan2(x, y) 返回 \(tanα\) \(=\) \(\frac{x}{y}\) 中的 \(α\)，同时满足 \(α\) \(\in \left [ -\pi , \pi \right ]\)。
当 \(y = 0\) 时， \(tanα\) 不存在，返回 \(0\) , 当 \(x = 0\) 时，返回 \(-1\)。

\[图2.2.1 \]

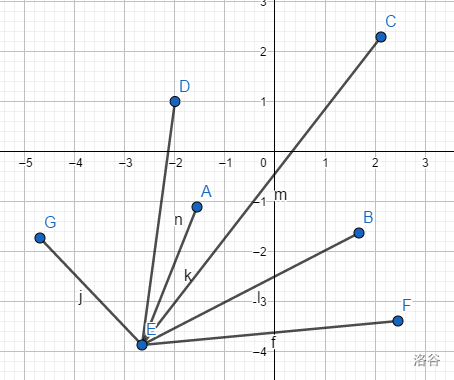
在上图中，每个点的极角是由点E到其他的点连成的直线 与 点E所在的与 \(x\) 轴平行的直线所成的夹角。
比如这个：

\[图2.2.2 \]

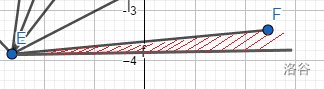
是点F的极角。

\[图2.2.3 \]

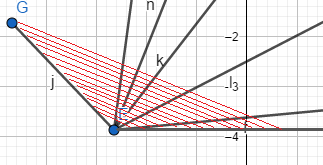
这个是点G的极角。

还是看上图2.2.1，排序结果是FBCADG，可以理解成从0度逆时针扫一圈。

直接快排实现就行，比较函数长这样：

inline bool cmp(const Cartesian &a, const Cartesian &b){
	double A = atan2((a.y - point[1].y), (a.x - point[1].x));
	double B = atan2((b.y - point[1].y), (b.x - point[1].x));

	if(A != B) return A < B;//按极角的大小递增排序 
	else if(a.x != b.x) return a.x < b.x;//如果极角相同，x坐标小的点在前
	else return a.y < b.y;//如果极角和x坐标都相同，y坐标小的在前 
}

---

之后，按照顺序依次访问所有点，判断可行性。

用图来讲：

\[图2.3.1 \]

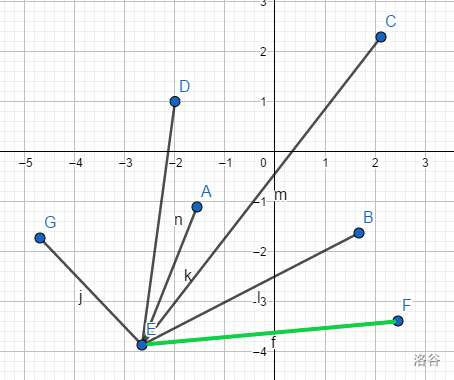
先把极角最小的E丢到凸包的栈里边，准备开始扫描。

\[图2.3.2 \]

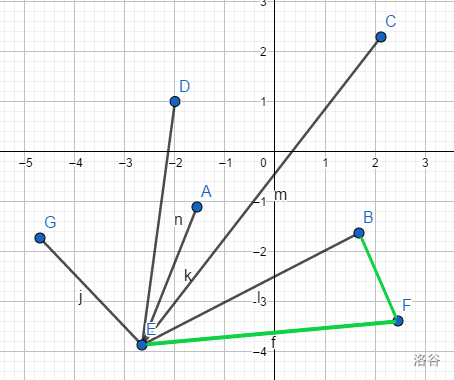
检查B是否在F的一侧（检查是不是凸多边形）。
这里检查到B可行，先加入到栈中。

\[图2.3.3 \]

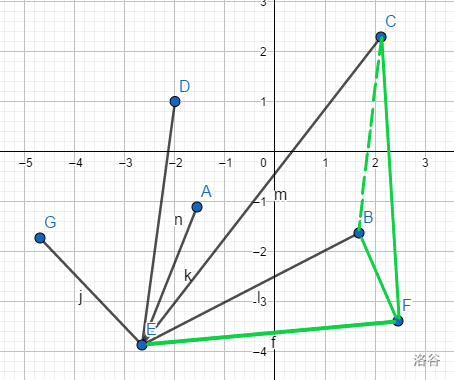
检查到C更加靠近外侧（如果加入B就会形成凹多边形，显然B在凸包中，而C不在）
然后把B点弹出栈，判断E和C的关（同判断B）

\[图2.3.4 \]

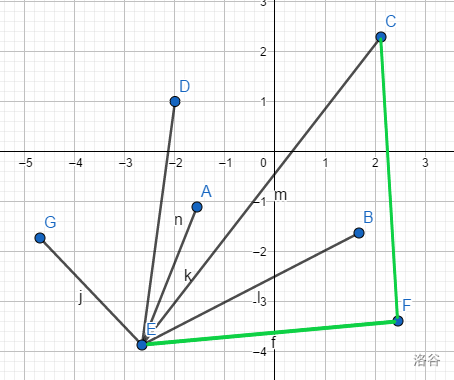
依次这么判断，最后所有凸包上的点都会在栈中

\[图2.3.5 \]

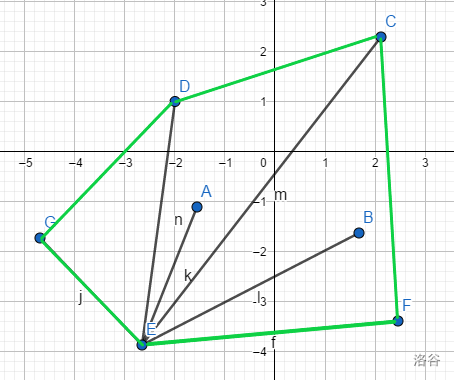
继续解决一些细节上的问题: 怎么计算一个节点是否在前一个点的一侧。
这就需要引入一个数学上的东西：叉积

\[图2.3.6 \]

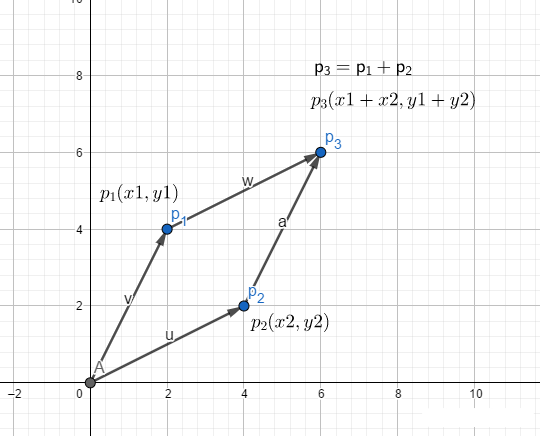
\(\vec{p_{1}}\times\vec{p_{2}}\) 即为平行四边形面积。

原理不会。看这个blog。

公式：\(\vec{p_{1}}\ast\vec{p_{2}} = {x_{1}}{y_{2}} - {x_{2}}{y_{1}}\)。

double Get_Cross(Cartesian a, Cartesian b, Cartesian c){
	return 1.0 * (b.x - a.x) * (c.y - a.y) - 1.0 * (b.y - a.y) * (c.x - a.x);
} //计算两向量的叉积

对于函数的意义，首先函数的正负是有特殊含义的：以C为参考点，如果大于0，则B在A的逆时针方向，反之，如果小于0，则B在A的顺时针方向，特殊的，当等于0，A、B、C三点共线。

详细的叉积可以看这位大佬的blog。

具体判断的话，还是上图

\[图2.3.6 \]

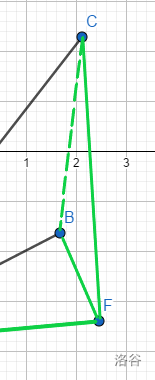
要判断点B是否在CF的外侧，计算\(\vec{FC} * \vec{FB}\) 。

B点坐标 \((1.68, -1.63)\) ,C点坐标 \((2.12, 2.29)\) ，F点坐标 \((2.46 -3.39)\) 。
\(\vec{FB} = (-0.78, 1.76)\) , \(\vec{FC} = (-0.34, 5.68)\) 。
\(\vec{FC} * \vec{FB} = 3.832 > 0\)

Code

#include<cmath> 
#include<cstdio>
#include<cstdlib>
#include<algorithm>

using namespace std;

const int MAXN = 1e5 + 10;
const double INF = 1145141919810;
int n, top;
double ans;

struct Cartesian{
	double x, y;
}point[MAXN], s[MAXN];

inline bool cmp(const Cartesian &a, const Cartesian &b){
	double A = atan2((a.y - point[1].y), (a.x - point[1].x));
	double B = atan2((b.y - point[1].y), (b.x - point[1].x));

	if(A != B) return A < B; //按极角的大小递增排序 
	else if(a.x != b.x) return a.x < b.x;  //如果极角相同，x坐标小的点在前
	else return a.y < b.y; //如果极角和x坐标都相同，y坐标小的在前 
}

double Get_Dis(Cartesian a, Cartesian b){
	return sqrt((1.0 * (a.x - b.x) * (a.x - b.x)) + (1.0 * (a.y - b.y) * (a.y - b.y)));
} //计算两点间距离

double Get_Cross(Cartesian a, Cartesian b, Cartesian c){
	return 1.0 * (b.x - a.x) * (c.y - a.y) - 1.0 * (b.y - a.y) * (c.x - a.x);
} //计算两向量的叉积

void Get_Bag(){ //造凸包 
	Cartesian point_left = (Cartesian){INF, INF};
	int pos;
	for(register int i = 1; i <= n; i++){
		if(point[i].y < point_left.y || (point[i].y == point_left.y && point[i].x < point_left.x)){
			point_left = point[i];
			pos = i;
		}
	} //寻找最左下角的点 
	swap(point[pos], point[1]);

	sort(point + 2, point + 1 + n, cmp); //按极角顺序排序 
	s[++top] = point[1], s[++top] = point[2];
	for(register int i = 3; i <= n;){
		if(top >= 2 && Get_Cross(s[top - 1], point[i], s[top]) >= 0)
			top--;
		else s[++top] = point[i++];
	}
	s[0] = s[top]; //记得凸包是闭合的
}

int main(){
	scanf("%d", &n);
	for(register int i = 1; i <= n; i++)
		scanf("%lf%lf", &point[i].x, &point[i].y);
	
	Get_Bag();

	while(top >= 1){
		Cartesian p1 = s[top];
		Cartesian p2 = s[top - 1];

		ans += Get_Dis(p1, p2);
		top--;
	}

	printf("%.2lf", ans);

	return 0;
} 

---

Andrew算法

不会，咕咕咕。