【BZOJ 3907】网格 组合数学

大家说他是卡特兰数，其实也不为过，一开始只是用卡特兰数来推这道题，一直没有怼出来，后来发现其实卡特兰数只不过是一种组合数学，我们可以退一步直接用组合数学来解决，这道题运用组合数的思想主要用到补集与几何法。

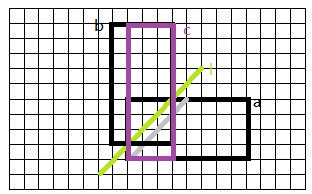
假设以矩形左下角为坐标原点，（以下所说路径均满足只能向右或向上走），我们假设原矩阵为a，那么他关于l(y=x+1)，对称矩形就是b（黑色），那么出现了c矩阵，他的长为n+1，宽为m-1，易知从(0,0)到(n,m)（a右上角）的路径（在矩形a内）的种数就是C(n+m,m)，然后我告诉你从(0,0)到(m-1,n+1)（c右上角）的路径（在矩形c内）种数C(n+m,m-1)，就是原矩阵中不合法路径个数，你不信很正常.....

那么让我们想一下。从(0,0)到(n,m)的不合法路径（在矩形a内）一定满足若干次碰到了l与a围成的三角型的边界之一——l在a内部分，然后在最后一次碰到后离开并驶向(n,m)，从(0,0)到(m-1,n+1)的路径（在矩形c内）均满足若干次碰到了l与a围成的三角型，然后在最后一次碰到后离开并驶向(m-1,n+1)，再然后我们发现在“离开”之前的走法满足以上两种路径可以吻合，那么“离开“之后呢——他离开时一定最后与l交于一点，那么我们发现在l上的任意整点（在a内部分）与(n,m)和(m-1,n+1)分别作为两个对角点形成的矩形全等，于是从一角到另一角的方案一一对应，于是证毕。

#include <cstdio>
#include <cstring>
const int P=10000;
struct Bigint{
  int a[5000];
  Bigint(){a[0]=a[1]=1;}
  inline friend Bigint operator - (Bigint a,Bigint b);
  inline friend Bigint operator * (Bigint a,int b);
  inline void operator -= (Bigint b){(*this)=(*this)-b;}
  inline void operator *= (int b){(*this)=(*this)*b;}
  inline void print();
}ans1,ans2;
inline void Bigint:: print(){
  printf("%d",a[a[0]]);
  for(int i=a[0]-1;i>0;--i)
    printf("%04d",a[i]);
}
inline Bigint operator - (Bigint a,Bigint b){
  for(int i=1;i<=a.a[0];++i){
    a.a[i]-=b.a[i];
    if(a.a[i]<0)
      a.a[i]+=P,a.a[i+1]--;
  }
  while(a.a[a.a[0]]==0)a.a[0]--;
  return a;
}
inline Bigint operator * (Bigint a,int b){
  int last=0;
  for(int i=1;i<=a.a[0];++i)
    a.a[i]=a.a[i]*b+last,last=a.a[i]/P,a.a[i]%=P;
  if(last)a.a[++a.a[0]]=last;
  return a;
}
int n,m;
int prime[P+10],len,mini[P+10];
bool isnot[P+10];
inline void get_prime(){
  for(int i=2;i<=P;++i){
    if(isnot[i]==false)prime[++len]=i,mini[i]=len;
    for(int j=1;prime[j]*i<=P;++j){
      isnot[prime[j]*i]=true,mini[prime[j]*i]=j;
      if(i%prime[j]==0)break;
    }
  }
}
int size[P];
int main(){
  scanf("%d%d",&n,&m),get_prime();
  for(int i=n+m,x;i>n;--i){
    x=i;
    while(mini[x])
      ++size[mini[x]],x/=prime[mini[x]];
  }
  for(int i=1,x;i<=m;++i){
    x=i;
    while(mini[x])
      --size[mini[x]],x/=prime[mini[x]];
  }
  for(int i=1;i<=len;++i)
    while(size[i])
      ans1*=prime[i],--size[i];
  for(int i=n+m,x;i>n+1;--i){
    x=i;
    while(mini[x])
      ++size[mini[x]],x/=prime[mini[x]];
  }
  for(int i=1,x;i<m;++i){
    x=i;
    while(mini[x])
      --size[mini[x]],x/=prime[mini[x]];
  }
  for(int i=1;i<=len;++i)
    while(size[i])
      ans2*=prime[i],--size[i];
  ans1-=ans2;
  ans1.print();
  return 0;
}