动态规划 | 背包问题 1068

 

这题对于我这种蒟蒻来说可谓是难度很大。作为pat少数的dp题，这题也有它的亮点。

①物品的价值和重量公用一个向量w

②如果最终dp[m]不等于m，说明无解

③要求结果（w序列）字典序最小

dp数组滚动示意图：

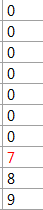
这题的标准答案是dp数组滚动。与普通无优化的背包问题不同，内循环：背包容量循环是从m（最大容量）递减到当前物品的容量。并且上个物品的dp值也是被记录在当前索引前面，起到了优化作用。

而“字典序最小”是通过① w数组递减排序 和 ②状态转移时使用<= 来实现的。普通的背包问题在转移时使用“<” 来判断，而这题进行了递减排序，字典序大的先被记录为解，如果出现了字典序小的方案，其dp值“==”上一个解的dp值，被重新记录，达到了字典序最小的效果。

下面演示“字典序最小”的工作机制：

●如果我们不进行递减排序，而是进行递增排序：

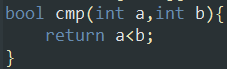
运行结果：

我们得到了字典序最大的解。

●我们进行递减排序：

 

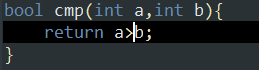
 其本质是新解对旧解的覆盖。

AC代码（滚动优化）：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>


#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 10010
#define MAX (1<<30)-1
#define V vector<int>

using namespace std;

const int maxn=10010;//总共的钱币(相当于物品数） 
const int maxv=110;//eva的钱币（相当于重量） 
int w[maxn];
int dp[maxv];
bool choice[maxn][maxv], flag[maxn];
bool cmp(int a,int b){
    return a>b;
}

int main(){
//    freopen("I:\\pat\\动态规划\\1068_1.txt","r",stdin);
    int n,m,i,j;
    I("%d%d",&n,&m);
    for(i=1;i<=n;i++) I("%d",&w[i]);
    sort(w+1,w+1+n,cmp);    //DESC排序
    for(i=1;i<=n;i++) {            //物品循环 
        for(int v=m;v>=w[i];v--){    //背包容量递减，直到和当前物品重量相等，退出循环 
            if(dp[v]<=dp[v-w[i]]+w[i]){    //如果放入物品是更优解 
                dp[v]=dp[v-w[i]]+w[i];
                choice[i][v]=1;            //记录放入的物品 
            }else{
                choice[i][v]=0;            //记录不放入的物品 
            } 
        }
    }
    if(dp[m]!=m){
        O("No Solution");
        return 0;
    }
    int k=n,num=0,v=m;
    while(k>=0){    //从最后搜索记录结果 
        if(choice[k][v]==1){
            flag[k]=1;
            v-=w[k];
            num++;
        }
        k--;
    }
    //因为 w 数组是逆序，所以逆序输出
    for(i=n;i>=1;i--) {
        if(flag[i]){
            O("%d",w[i]);
            num--;
            if(num>0) O(" ");
        }
    }
    return 0;
}