一步一步编写AVL树
第一步:定义结构体
typedef struct Node{ int d; //data int h=1; //height struct Node* l=NULL; struct Node* r=NULL; Node(int d=0):d(d){ } }Node;
这个结构体和常规的二叉树结构体很相似。但是不同的是多了个属性“h”(height)。用这个属性来记录结点的高度,叶子结点为1,空结点为0 。
第二部:编写BST树的插入函数
Node* insert(Node* p,int v){ Node * node=new Node(v); if(!p){ return node; } if(v < p->d){ //左子树 if(p->l){ p->l=insert(p->l,v); }else{ p->l=node; } }else{ if(p->r){ p->r=insert(p->r,v); }else{ p->r=node; } } // setHeight(p); //平衡旋转代码 //end of 平衡旋转代码 return p; }
第三步:编写高度获取与设置的辅助函数
高度获取:
int getHeight(Node* node){ if(node) return node->h; //如果非空返回这个结点的height return 0; //空节点的高度是0 }
高度设置:
void setHeight(Node* node){ //取左右子树高度的最大值,记得+1 node->h=max(getHeight(node->l),getHeight(node->r))+1; }
第四步:编写平衡旋转函数
当左右子树的height相差为2时,就要调用平衡旋转函数进行旋转。一共有4种旋转模式:
(注:一下图片采用自博客:http://www.cnblogs.com/Camilo/p/3917041.html,如果侵权请联系我删除)
左子树左结点引起的不平衡:
Node* LL(Node* node){ Node* re=node->l; node->l=re->r; re->r=node; setHeight(node); //注意:先进行这一步。因为node是re的子结点,从下往上调整 setHeight(re); return re; }
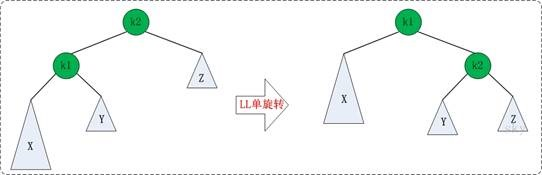
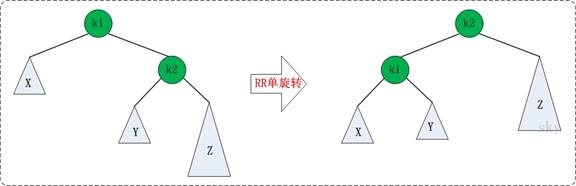
右子树右结点引起的不平衡:
Node* RR(Node* node){ Node* re=node->r; node->r=re->l; re->l=node; setHeight(node); setHeight(re); return re; }
(注:编写技巧是在LL函数的基础上,把所有的r写成l,把所有的l写成r,轮换对称思想)
左子树右结点引起的不平衡:
Node* LR(Node* node){ node->l=RR(node->l); node=LL(node); return node; }

右子树左结点引起的不平衡:
Node* RL(Node* node){ node->r=LL(node->r); node=RR(node); return node; }

第五步:在BST树的插入函数中编写平衡旋转代码:
Node* insert(Node* p,int v){ Node * node=new Node(v); if(!p){ return node; } if(v < p->d){ //左子树 if(p->l){ p->l=insert(p->l,v); }else{ p->l=node; } }else{ if(p->r){ p->r=insert(p->r,v); }else{ p->r=node; } } setHeight(p); //平衡旋转代码 if(getHeight(p->l)-getHeight(p->r)==2){ //左子树不平衡 if(getHeight(p->l->l)>getHeight(p->l->r)){//左结点不平衡 p=LL(p); }else{ //右结点不平衡 p=LR(p); } } if(getHeight(p->r)-getHeight(p->l)==2){ //右子树不平衡 if(getHeight(p->r->l)>getHeight(p->r->r)){//左结点不平衡 p=RL(p); }else{ //右结点不平衡 p=RR(p); } } //end of 平衡旋转代码 return p; }
打个OJ测试一下:1123. Is It a Complete AVL Tree
AC代码:
#include <stdio.h> #include <queue> #include <algorithm> using namespace std; typedef struct Node{ int d; //data int h=1; //height struct Node* l=NULL; struct Node* r=NULL; Node(int d=0):d(d){ } }Node; int getHeight(Node* node){ if(node) return node->h; //如果非空返回这个结点的height return 0; //空节点的高度是0 } void setHeight(Node* node){ //取左右子树高度的最大值,记得+1 node->h=max(getHeight(node->l),getHeight(node->r))+1; } Node* LL(Node* node){ Node* re=node->l; node->l=re->r; re->r=node; setHeight(node); //注意:先进行这一步。因为node是re的子结点,从下往上调整 setHeight(re); return re; } Node* RR(Node* node){ Node* re=node->r; node->r=re->l; re->l=node; setHeight(node); setHeight(re); return re; } Node* LR(Node* node){ node->l=RR(node->l); node=LL(node); return node; } Node* RL(Node* node){ node->r=LL(node->r); node=RR(node); return node; } Node* insert(Node* p,int v){ Node * node=new Node(v); if(!p){ return node; } if(v < p->d){ //左子树 if(p->l){ p->l=insert(p->l,v); }else{ p->l=node; } }else{ if(p->r){ p->r=insert(p->r,v); }else{ p->r=node; } } setHeight(p); //平衡旋转代码 if(getHeight(p->l)-getHeight(p->r)==2){ //左子树不平衡 if(getHeight(p->l->l)>getHeight(p->l->r)){//左结点不平衡 p=LL(p); }else{ //右结点不平衡 p=LR(p); } } if(getHeight(p->r)-getHeight(p->l)==2){ //右子树不平衡 if(getHeight(p->r->l)>getHeight(p->r->r)){//左结点不平衡 p=RL(p); }else{ //右结点不平衡 p=RR(p); } } //end of 平衡旋转代码 return p; } int cnt=0; int main(){ // freopen("I:\\pat\\树\\AVL\\1123_2.txt","r",stdin); int n,t; scanf("%d",&n); Node * root; for(int i=0;i<n;i++){ scanf("%d",&t); root=insert(root,t); } queue<Node*> q; q.push(root); bool findNull=0; bool yes=1; bool after=0; while(!q.empty()){ Node* t=q.front(); q.pop(); printf("%d",t->d); cnt++; if(cnt!=n) printf(" "); if(t->l){ q.push(t->l); if(after) yes=0; } else after=1; if(t->r){ q.push(t->r); if(after) yes=0; } else after=1; } puts(""); puts(yes?"YES":"NO"); return 0; }





