数学问题-解方程

高斯消元法

模板：

void gauss(){
    int i,j,k,m;
    double t; 
    for(i=0;i<n;i++){    //对于每一行 
        //归一
        t=a[i][i];
        for(j=i;j<=n;j++)
            a[i][j]/=t;
        //相减
        for(j=0;j<n;j++) if(j!=i){        //扫描被减的每一行 
            t=a[j][i];    //倍减系数
            for(k=i;k<=n;k++){
                a[j][k]-=a[i][k]*t;
            }
        }
    }
}

完整代码：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>

#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 100
#define MAX 0x06FFFFFF
#define V vector<int>

using namespace std;

double a[LEN][LEN];
int n;

void printMat(){
    int i,j;
    FF(i,n){
        FF(j,n+1) 
            printf("%.0lf\t",a[i][j]);
        puts("");
    }
}

void gauss(){
    int i,j,k,m;
    double t; 
    for(i=0;i<n;i++){    //对于每一行 
        //归一
        t=a[i][i];
        for(j=i;j<=n;j++)
            a[i][j]/=t;
        //相减
        for(j=0;j<n;j++) if(j!=i){        //扫描每一行 
            t=a[j][i];    //倍减系数
            for(k=i;k<=n;k++){
                a[j][k]-=a[i][k]*t;
            }
        }
    }
}



int main(){
    freopen("D:\\CbWorkspace\\数学问题\\高斯消元法.txt","r",stdin);
    int i,j;
    I("%d",&n);
    for(i=0;i<n;i++){
        for(j=0;j<=n;j++){
            I("%lf",&a[i][j]);
        }
    }
    gauss();
    for(i=0;i<n;i++){
        printf("x%d = %.2lf\n",i+1,a[i][n]);
    }
    return 0;
    
    
}

测试数据：

3
1 1 1 0
1 2 4 -1
1 3 9 0

注：3行3列的系数矩阵，加上一列向量b，构成的增广矩阵

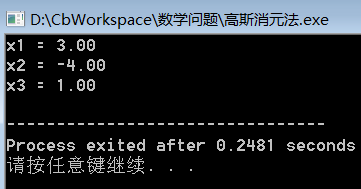
测试效果：

 

---