动态规划-最长公共子序列与最长公共子串

1.最长公共子序列

参考博客：

http://blog.csdn.net/hrn1216/article/details/51534607

http://blog.csdn.net/u013074465/article/details/45392687

代码：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>


#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 101
#define MAX 1<<30
#define V vector<int>

using namespace std;

int a[LEN],b[LEN]; 
int dp[LEN][LEN];
int N,M;
vector<vector<int> > ans;

void printDP(){
    int i,j;
    F(i,1,N+1){
        F(j,1,M+1){
            O("%d\t",dp[i][j]);
        }
        OL("\n");
    }
}

void buildLCS(int x,int y,V vec){
    while(x>0 && y>0){
        if(a[x]==b[y]){
            vec.push_back(a[x]);
            x--;y--;
        }else{
            if(dp[x-1][y]>dp[x][y-1]){
                x--;
            }else if(dp[x-1][y]<dp[x][y-1]){
                y--;
            }else{
                buildLCS(x,y-1,vec);
                x--;
            }
        }
    }
    int i=vec.size()-1;
    while(i>=0){
        O("%d ",vec[i]);
        i--;
    }
    OL("");
}

int main(){
    freopen("LCS.txt","r",stdin);
    int i,j;
    scanf("%d",&N);
    F(i,1,N+1) I("%d",&a[i]);
    scanf("%d",&M);
    F(i,1,M+1) I("%d",&b[i]);
    F(i,1,N+1){ 
        F(j,1,M+1){
            if(a[i]==b[j])
                dp[i][j]=dp[i-1][j-1]+1;
            else
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
        }
    }
    printDP();
    O("最长公共子序列长度: %d\n",dp[N][M]);
    V vec;
    buildLCS(N,M,vec);
    return 0;
}

测试数据：

9
3 5 7 4 8 6 7 8 2
8
1 3 4 5 6 7 7 8

 

---

2.最长公共子串

代码：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>


#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 101
#define MAX 1<<30
#define V vector<int>

using namespace std;

int a[LEN],b[LEN]; 
int dp[LEN][LEN];
int N,M;
vector<vector<int> > ans;

void printDP(){
    int i,j;
    F(i,1,N+1){
        F(j,1,M+1){
            O("%d\t",dp[i][j]);
        }
        OL("\n");
    }
}

int main(){
    freopen("最长公共子串.txt","r",stdin);
    int i,j;
    scanf("%d",&N);
    F(i,1,N+1) I("%d",&a[i]);
    scanf("%d",&M);
    F(i,1,M+1) I("%d",&b[i]);
    int mx,my,mlen=0;
    F(i,1,N+1){ 
        F(j,1,M+1){
            if(a[i]==b[j]){
                dp[i][j]=dp[i-1][j-1]+1;
                if(mlen<dp[i][j]){
                    mlen=dp[i][j];
                    mx=i;
                    my=j;
                }
            }
            else
                dp[i][j]=0;
        }
    }
    printDP();
    O("最长公共子序列长度: %d\n",mlen);
    V ans;
    while(dp[mx][my]){
        ans.insert(ans.begin(),a[mx]);
        mx--;my--;
    }
    FF(i,ans.size()){
        printf("%d ",ans[i]);
    }
    return 0;
}

测试数据：

9
3 5 7 4 8 6 7 8 2
8
1 3 4 8 6 7 7 8

 

---

 

3.相似基因

代码：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>


#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 110
#define MAX 1<<30
#define V vector<int>

using namespace std;


int dp[LEN][LEN];
int mat[5][5]={
{5,-1,-2,-1,-3},
{-1,5,-3,-2,-4},
{-2,-3,5,-2,-2},
{-1,-2,-2,5,-1},
{-3,-4,-2,-1,0}};

int to(char ch){
    if(ch=='A') return 0;
    else if(ch=='C') return 1;
    else if(ch=='G') return 2;
    else if(ch=='T') return 3;
    else return 4;
}

int main(){
//    freopen("相似基因.txt","r",stdin);
    int an,bn,i,j;
    char buf[LEN];
    string a,b;
    I("%d",&an);
    I("%s",buf);
    a=buf;
    a.insert(0,"#");
    I("%d",&bn);
    I("%s",buf);
    b=buf;
    b.insert(0,"#");
    memset(dp,-127,sizeof(dp));
    dp[0][0]=0;
    for(i=0;i<=an;i++){
        for(j=0;j<=bn;j++){
            if(i && j) dp[i][j]=max(dp[i][j],dp[i-1][j-1] + mat[to(a[i])][to(b[j])]  );
            if(i) dp[i][j]=max(dp[i][j],dp[i-1][j] + mat[to(a[i])][4]  );
            if(j) dp[i][j]=max(dp[i][j],dp[i][j-1] + mat[4][to(b[j])]  );    
        }
    }
    printf("%d",dp[an][bn]);
    return 0;
}

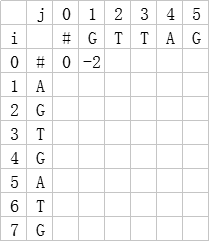
理解： 在边界条件的限制下，有三种情况：

1. 当前基因与对象基因进行匹配，　　　　　　　　＝ｄｐ［ｉ－１］［ｊ－１］＋ｆ（ｉ，ｊ）

2. 当前基因放弃匹配，插入一个“-”（空符号）　　　＝ｄｐ［ｉ－１］［ｊ］＋ｆ（ｉ，∅）

3. 对象基因放弃匹配，插入一个“-”（空符号）　　　＝ｄｐ［ｉ］［ｊ－１］＋ｆ（∅，ｊ）

基本思路与LCS相同

 

---