回溯法 | n皇后问题
今早上看了一篇英语阅读之后,莫名有些空虚寂寞冷。拿出算法书,研读回溯法。我觉得n皇后问题完全可以用暴力方式,即先对n个数进行全排列,得到所有结果的下标组合,问题规模为n!。
全排列花了比较久的时间才编写出来。主要是没有找对思路。最终我想到了递归,即对4个数进行全排列可以化为把【对3个数进行了全排列】的结果拿出来,在下标为1-4的位置上各插上一个数,一次类推。于是我编写了全排列类:
1 //全排列 2 class Arrangment{ 3 int[][]ans; 4 Arrangment(){} 5 Arrangment(int[] nums){ 6 ans=createA(nums.length,nums); 7 } 8 void printNums(int[][] nums){ 9 int row=nums.length; 10 int col=nums[0].length; 11 int i,j; 12 for(i=0;i<row;i++){ 13 for(j=0;j<col;j++) 14 System.out.print(nums[i][j]+" "); 15 System.out.print("\n"); 16 } 17 } 18 int[][]createA(int rank,int []nums){ 19 int[][] re; 20 if(rank>1){ 21 int[][] pre=createA(rank-1,nums); 22 int row=pre.length; 23 int col=nums.length; 24 re=new int[row*rank][rank]; 25 int index=0; 26 int i,j,k,m; 27 for(i=0;i<rank;i++){ 28 for(j=0;j<row;j++){ 29 for(k=0,m=0;k<rank ;k++){ 30 if(k==i){//如果列下标等于i(在0~rank)中循环 31 re[index][k]=nums[rank-1]; 32 int a; 33 a=0; 34 }else{ 35 re[index][k]=pre[j][m]; 36 m++; 37 } 38 } 39 index++; 40 } 41 } 42 43 } 44 else{ 45 re=new int[1][1]; 46 re[0][0]=nums[0]; 47 } 48 return re; 49 } 50 private int factorial(int n){ 51 int re=1; 52 while(n>=1) 53 re*=(n--); 54 return re; 55 } 56 }
使用这个全排列类,就可以构造所有的问题的求解空间了。
暴力求解算法:
1 class N_Queens{ 2 int n; 3 N_Queens(int inN){ 4 n=inN; 5 } 6 List<int[]> solved =new ArrayList<int[]>(); 7 void solveByBrutal(){//穷举求解 8 9 boolean isComplied(int[] nums,int len){ 10 int i,j; 11 for(i=0;i<len-1;i++) 12 for(j=i+1;j<len;j++){ 13 int a=Math.abs(i-j); 14 int b=Math.abs(nums[i]-nums[j]); 15 if(a==b || b==0) 16 return false; 17 } 18 return true; 19 } 20 }
然后我开始研究怎么使用【回溯法】进行解题。我看了严奶奶书上的伪代码,以及树形结构实例,感触颇深。原来我以为这个问题和8数码问题一样需要进行树的按层遍历,已经使用队列结构的,但是他既然使用了一种递归的思想,并且是深度优先的。用递归的入栈出栈,在【剪掉枝丫】(问题不可解)和【找到一个解】之后,自动的求下一个解。
回溯法代码:
1 class N_Queens{ 2 int n; 3 N_Queens(int inN){ 4 n=inN; 5 } 6 List<int[]> solved =new ArrayList<int[]>(); 7 void solveByBackTrace(){ 8 int[] nums=null; 9 trial(nums,0); 10 } 11 void trial(int [] nums,int i){//棋盘上的前i行已经放置了【符合条件】的棋子 12 if(i<n){ 13 int j,k; 14 //第i行进行放置 15 for(j=0;j<n;j++){//在第j列上进行遍历 16 int[] node=new int[n];//新建结点 17 for(k=0;k<i;k++) 18 node[k]=nums[k];//拷贝父结点 19 node[i]=j;//第i行第j列上放上一个皇后 20 if(isComplied(node,i+1)){//符合条件 21 trial(node,i+1);//扩展它的子节点 22 } 23 } 24 }else{ 25 solved.add(nums); 26 } 27 } 28 29 boolean isComplied(int[] nums,int len){ 30 int i,j; 31 for(i=0;i<len-1;i++) 32 for(j=i+1;j<len;j++){ 33 int a=Math.abs(i-j); 34 int b=Math.abs(nums[i]-nums[j]); 35 if(a==b || b==0) 36 return false; 37 } 38 return true; 39 } 40 }
完整代码:

1 import java.util.*; 2 3 4 public class Main { 5 6 public static void main(String[] args) { 7 while(true){ 8 System.out.print("请输入皇后的数目:"); 9 Scanner scan=new Scanner(System.in); 10 int n=scan.nextInt(); 11 N_Queens problem=new N_Queens(n); 12 int []nums={1,2,3}; 13 problem.isComplied(nums, 2); 14 problem.solveByBrutal(); 15 problem.PrintChecker(); 16 } 17 } 18 19 } 20 21 //全排列 22 class Arrangment{ 23 int[][]ans; 24 Arrangment(){} 25 Arrangment(int[] nums){ 26 ans=createA(nums.length,nums); 27 } 28 void printNums(int[][] nums){ 29 int row=nums.length; 30 int col=nums[0].length; 31 int i,j; 32 for(i=0;i<row;i++){ 33 for(j=0;j<col;j++) 34 System.out.print(nums[i][j]+" "); 35 System.out.print("\n"); 36 } 37 } 38 int[][]createA(int rank,int []nums){ 39 int[][] re; 40 if(rank>1){ 41 int[][] pre=createA(rank-1,nums); 42 int row=pre.length; 43 int col=nums.length; 44 re=new int[row*rank][rank]; 45 int index=0; 46 int i,j,k,m; 47 for(i=0;i<rank;i++){ 48 for(j=0;j<row;j++){ 49 for(k=0,m=0;k<rank ;k++){ 50 if(k==i){//如果列下标等于i(在0~rank)中循环 51 re[index][k]=nums[rank-1]; 52 int a; 53 a=0; 54 }else{ 55 re[index][k]=pre[j][m]; 56 m++; 57 } 58 } 59 index++; 60 } 61 } 62 63 } 64 else{ 65 re=new int[1][1]; 66 re[0][0]=nums[0]; 67 } 68 return re; 69 } 70 private int factorial(int n){ 71 int re=1; 72 while(n>=1) 73 re*=(n--); 74 return re; 75 } 76 } 77 78 class N_Queens{ 79 int n; 80 N_Queens(int inN){ 81 n=inN; 82 } 83 List<int[]> solved =new ArrayList<int[]>(); 84 void solveByBrutal(){//穷举求解 85 int i; 86 int indexs[]=new int[n]; 87 for(i=0;i<n;i++) indexs[i]=i; 88 Arrangment solve=new Arrangment(indexs); 89 int[][] solceSpace=solve.ans;//构造所有解空间 90 solved.clear(); 91 for(i=0;i<solceSpace.length;i++){ 92 if(isComplied(solceSpace[i],n)) 93 solved.add(solceSpace[i]); 94 } 95 int a; 96 a=0; 97 } 98 void solveByBackTrace(){ 99 int[] nums=null; 100 trial(nums,0); 101 } 102 void trial(int [] nums,int i){//棋盘上的前i行已经放置了【符合条件】的棋子 103 if(i<n){ 104 int j,k; 105 //第i行进行放置 106 for(j=0;j<n;j++){//在第j列上进行遍历 107 int[] node=new int[n];//新建结点 108 for(k=0;k<i;k++) 109 node[k]=nums[k];//拷贝父结点 110 node[i]=j;//第i行第j列上放上一个皇后 111 if(isComplied(node,i+1)){//符合条件 112 trial(node,i+1);//扩展它的子节点 113 } 114 } 115 }else{ 116 solved.add(nums); 117 } 118 } 119 120 boolean isComplied(int[] nums,int len){ 121 int i,j; 122 for(i=0;i<len-1;i++) 123 for(j=i+1;j<len;j++){ 124 int a=Math.abs(i-j); 125 int b=Math.abs(nums[i]-nums[j]); 126 if(a==b || b==0) 127 return false; 128 } 129 return true; 130 } 131 132 public String toString(){ 133 int i,j; 134 String str=new String(""); 135 for(i=0;i<solved.size();i++){ 136 int [] out=solved.get(i); 137 for(j=0;j<out.length;j++){ 138 str+=out[j]; 139 str+=" "; 140 } 141 str+="\n"; 142 } 143 return str; 144 } 145 void PrintChecker(){ 146 int i,j,k; 147 String out=new String(); 148 for(i=0;i<solved.size();i++){ 149 int[] nums=solved.get(i); 150 for(j=0;j<nums.length;j++){ 151 int l=nums[j]; 152 int r=nums.length-1-nums[j]; 153 for(k=0;k<l;k++) out+="□"; 154 out+="■"; 155 for(k=0;k<r;k++) out+="□"; 156 out+="\n"; 157 } 158 out+="\n"; 159 } 160 System.out.print(out); 161 } 162 }
输出结果:
4皇后:
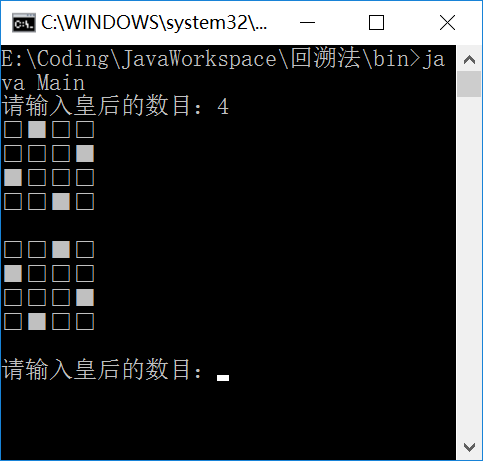
8皇后:
10皇后: