9大背包第一弹 | 01背包
今天学习01背包。因为01背包在暑假学习过,所以上网看了一下文章,就能写出来了。主要还是一种动态规划的思想,设置背包的【容量】进行增长,【物品】进行增长。只要满足【当前物品】的【价值】=max{
不放入【当前物品】的价值,
从【当前容量】中腾出【当前物品】的【重量】的物品。即丢弃掉掉一些东西,是【当前物品】能放入【当前容量】的背包中。
}
表达能力有限,附上学习链接:动态规划之01背包问题(最易理解的讲解)
不过感觉这篇文章的求解矩阵画的有问题。
我的Java代码:
1 import java.util.*; 2 3 public class Main { 4 5 public static void main(String[] args) { 6 // TODO Auto-generated method stub 7 int []w={2,2,6,5,4}; 8 int []v={6,3,5,4,6}; 9 int weight=10; 10 _01package problem=new _01package(w,v,weight); 11 12 13 } 14 15 } 16 17 class _01package{ 18 //价值、重量 19 int [][] matrix; 20 List<Integer> solve=new ArrayList<Integer>(); 21 _01package(int [] w,int [] v,int weight){ 22 23 int i,j; 24 int len=w.length; 25 matrix=new int[len+1][weight+1];//构建求解数组 26 for(i=0;i<weight+1;i++) matrix[0][i]=0;//第一行为0 27 for(i=0;i<len+1;i++) matrix[i][0]=0;//第一列为0 28 //动态规划 29 for(i=1;i<len+1;i++){ //从上到下【不断将物品放入背包】【i】代表物品 30 for(j=1;j<weight+1;j++){ //从左到右【背包的容量不断扩充】【j】代表当前容量 31 if(j>w[i-1]){//【当前背包容量】比【将要放入的物品】的【重量】大 32 matrix[i][j]=Math.max 33 (matrix[i-1][j], //选择不放 34 matrix[i-1][j-w[i-1]]+v[i-1]); //让背包腾出w[i-1],即【当前物品】的【重量】的空间,选择放入 35 }else{ //放不进。拷贝【上一个物品】的重量 36 matrix[i][j]=matrix[i-1][j]; 37 } 38 } 39 } 40 System.out.println("求解矩阵:"); 41 System.out.print(this); 42 //回溯 43 j=weight;//最后一列 44 for(i=len;i>0;i--){//对行进行遍历 45 if(matrix[i][j]>matrix[i-1][j]){//增减物品时,价值增加了。说明放入了物品 46 j-=w[i-1]; 47 solve.add(i); 48 } 49 } 50 System.out.print("应该放入背包的物品:"); 51 for(i=0;i<solve.size();i++) System.out.print(solve.get(i)+" "); 52 System.out.println(); 53 } 54 55 public String toString(){ 56 int row = matrix.length;//行数 57 int col =matrix[0].length;//列数 58 String str=new String(""); 59 int i,j; 60 for(i=0;i<row;i++){ 61 for(j=0;j<col;j++){ 62 str+=Integer.toString(matrix[i][j]); 63 str+="\t"; 64 } 65 str+="\n\n"; 66 } 67 return str; 68 } 69 }
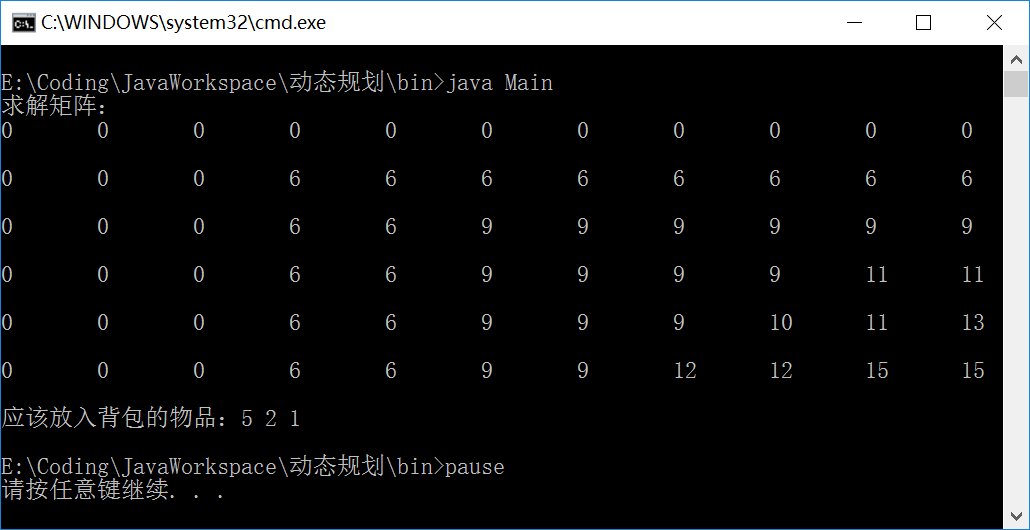
求解矩阵:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 6 6 6 6 6 6 6 0 0 0 6 6 9 9 9 9 9 9 0 0 0 6 6 9 9 9 9 11 11 0 0 0 6 6 9 9 9 10 11 13 0 0 0 6 6 9 9 12 12 15 15
运行结果: