进制的本质

进制的本质

进制

「进制」也就是 「进位制」，其实是一种记数的方式，也称为「进位计数制」，是用一组固定的符号和统一的规则来表示所有数值的方法。对于任何一种进制—X进制，就表示每一位置上的数运算时都是逢X进一位。一进制是逢一进一，二进制是逢二进一，八进制是逢八进一，十进制是逢十进一，十六进制是逢十六进一，以此类推，X进制就是逢X进位

# 一进制 1~20
1
1 1
1 1 1
1 1 1 1
...

# 三进制 1~20
0 1 2
10 11 12
20 21 22
100 101 102
110 111 112
120 121 122
...

# 七进制 
0 1 2 3 4 5 6
10 11 12 13 14 15 16
20 21 22 23 24 25 26
...

对于任何一个数，我们可以用不同的进位制来表示，他们是等价的，只是表示形式不同而已

进制实际上就是一组符号，任何人都可以用任意的符号去定制自己的进制。因此，数字与符号并无本质区别

进制运算

进制运算的本质就是写表和查表

这里先写出一个八进制的表，在正常的八进制中有0、1、2、3、4、5、6、7这八个元素，它们所表示出来的数如下：

接着尝试用八进制计算下面的结果：

2 + 3 = ？
4 + 5 = ？
2 * 3 = ？
4 * 5 = ？

加法法则：

• 2 + 3其实就是在2的基础上，往后数3个数，参照上表可知，2往后的第三个数为5，故2 + 3 = 5

• 依照前面的思路，4 + 5从4往后数5个数，便是11，所以4 + 5 = 11

到此，可以做出八进制的加法表：

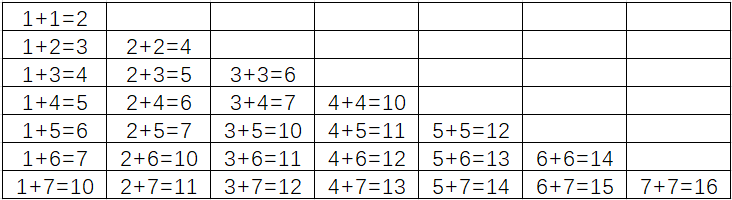
乘法法则：

• 加法法则就是往后数个数，那同理，乘法法则就是往后数成倍的个数，2 * 3就是3个2相加，也就是从2往后数4个数，便为6，所以2 * 3 = 6
• 同上，4 * 5 就是从4往后数16个数，即为24，故4 * 5 = 24

到此，可以做出八进制的乘法表：

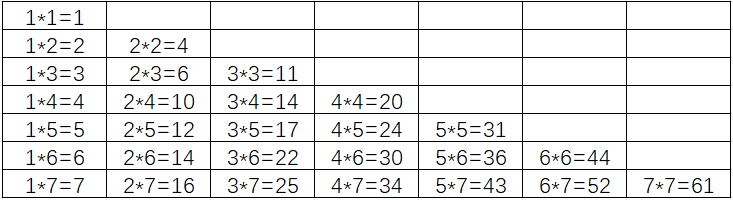
接下来尝试计算以下结果：

277 + 333 = ?
276 * 54 = ?
234 / 4 = ?

• 277 + 333：我们先从最后一个位看，是7加3，查表得12，故最后一位结果为2，1向前进位；再看倒数第二个位，还是7加3，加上刚刚进位的1，查表得13，所以倒数第二个位的结果为3，1向前进位；最后看倒数第三个位，2加3再加上刚进位的1，查表得6，故倒数第三个位的结果为6，没有进位。所以最终结果为632

• 276 * 54：先算276乘4，从最后一个位看起，是6乘4，查表得30，故最后一个位的结果为0，3向前进位；再看倒数第二个位，为7乘4，再加上刚刚进位的3，查表得37，故倒数第二个位的结果为7，3向前进位；最后看倒数第三个位，2乘4再加上刚刚进位的3，查表得13，所以276乘4的结果为1370；再算276乘5，同理得1666；最后1370与1666错位相加（1370+16660）得到最终结果20250

• 234 / 4：除法的本质其实就是看除数乘以多少能够成为被除数或最接近被除数。先从被除数第一个位看起，发现2不够被4除，所以我们再看23，发现此时够除，于是查表寻找4乘以多少最接近23，得4 * 4 = 20，故第一个位的结果为4；然后剩下34除以4，查表得4 * 7 = 34，故第二个位的结果为7。所以最终结果为47

结论：无论是什么进制，本身都是有一套完美的运算体系的，我们都可以通过列表的方式将它计算出来