双指针之快慢指针

快慢指针（Floyd 判圈法）

1、简介

对于链表找环路的问题，有一个通用的解法——快慢指针（Floyd 判圈法）。

给定两个指针，分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步，slow 前进一步。如果 fast
可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存在某个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点

2、推导

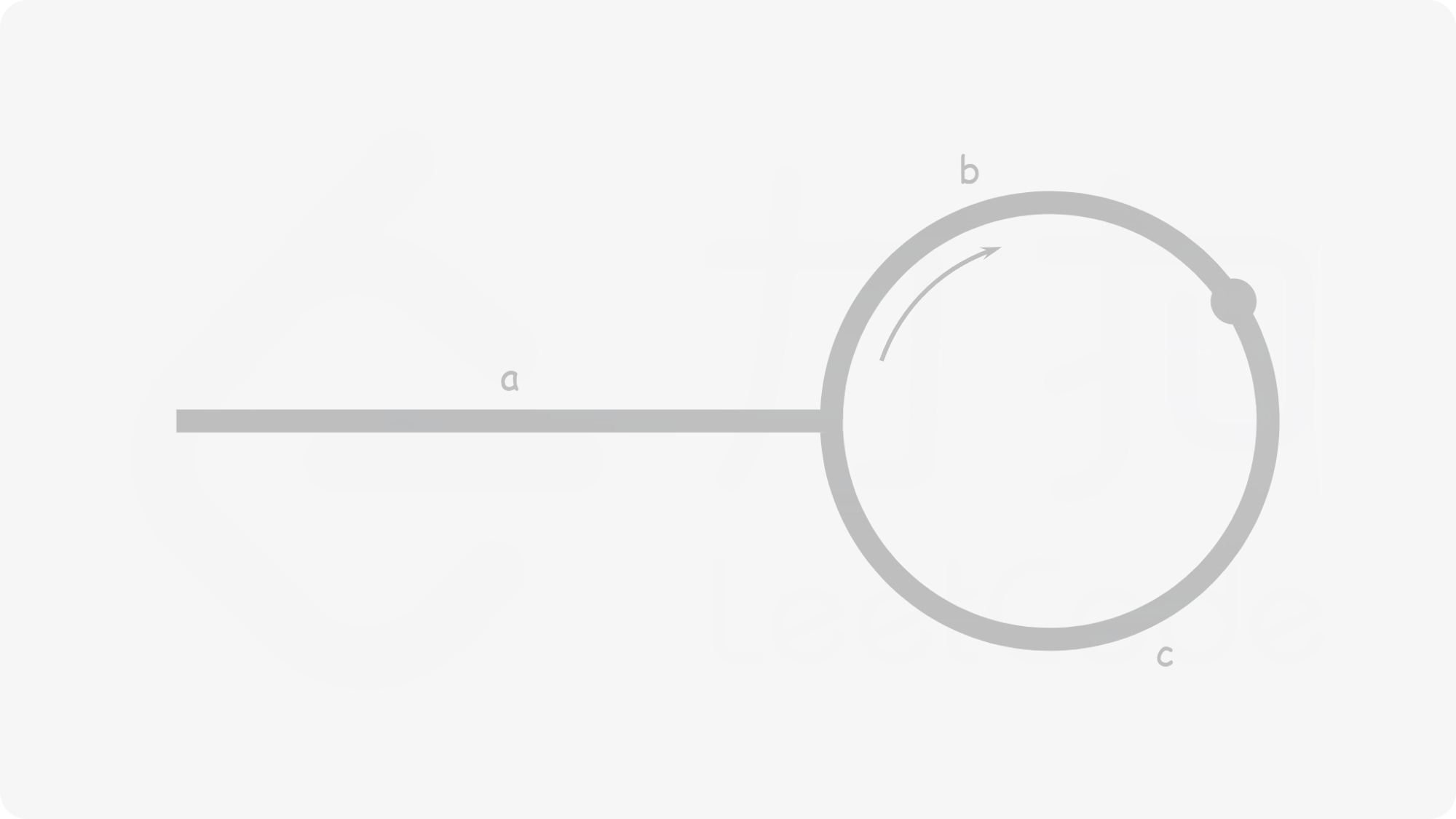
如上图所示，设链表中入环前的部分长为 $a$，slow 指针入环后，又走了 $b$ 的距离与 fast 相遇，剩下距离 $c$ 才走完当前环

此时，fast 比 slow 多走了环的 $n$ 圈，fast 走过的总距离为 $a + n(b + c) + b$，slow 走过的总距离为 $a + b$

根据题意，fast 走过的距离恒为 slow 的两倍，故 $a + n(b + c) + b = 2(a + b)$ ，即 $a = c + (n - 1)(b + c)$

从上式我们可以看出，从相遇点到入环点的距离加上 $n - 1$ 圈的环长，恰好等于从链表头部到入环点的距离。此时，我们再让 fast 指针指向链表的头部，随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution 
{
public:
    ListNode *detectCycle(ListNode *head) 
    {
        ListNode* fast = head;
        ListNode* slow = head;
        do 
        {
            if (fast == nullptr || fast->next == nullptr)
                return nullptr;
            fast = fast->next->next;
            slow = slow->next;
        } while (fast != slow);
        fast = head;
        while (fast != slow)
        {
            fast = fast->next;
            slow = slow->next;
        }
        return fast;
    }
};

---

如果您觉得阅读本文对您有帮助，请点一下“推荐”按钮，您的“推荐”将是我最大的写作动力！欢迎各位转载，但是未经作者本人同意，转载文章之后必须在文章页面明显位置给出作者和原文连接，否则保留追究法律责任的权利。