PCA（主成分分析）

PCA（主成分分析）

预备知识

• 线性代数：线性代数的本质

• 样本均值：$\bar x = \frac{1}{n}\sum_{i=1}^n x_i$

• 样本方差：$Var(x) = \frac{1}{n}\sum_{i=1}^n(x_i-\bar x)^2$

• 样本X和样本Y的协方差：$Cov(X,Y) = \frac{1}{n}\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)$

• 协方差矩阵：$C = \frac{1}{n}XX^T = \begin{pmatrix} \frac{1}{n}\sum_{i=1}^na_i^2&\frac{1}{n}\sum_{i=1}^na_ib_i\\ \frac{1}{n}\sum_{i=1}^na_ib_i&\frac{1}{n}\sum_{i=1}^nb_i^2\\ \end{pmatrix}$

简介

• 在多元统计分析中，主成分分析（Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，这些不相关的变量称为主成分（Principal Components）。
• PCA的主要思想是将N维特征映射到K维上，这K维是全新的正交特征也被称为主成分，是在原有N维特征的基础上重新构造出来的N维特征。
• PCA主要是用来将高维数据降为低维数据，并保留主要成分的。

数据降维

• 降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。

• 在一般情况下，如果要将M个N维向量变换到由R个N维向量表示的新空间中，那么首先寻找R个N维基并按行组成矩阵$A$，然后将原向量按列组成矩阵$B$，则两矩阵的乘积$AB$就是变换结果，其中$AB$的第n列为$A$中第n列变换后的结果

  其数学表达式为：

  $$\begin{pmatrix} p_1\\ p_2\\ \vdots\\ p_R \end{pmatrix} \begin{pmatrix} a_1&a_2&\cdots&a_M\\ \end{pmatrix} = \begin{pmatrix} p_1a_1&p_1a_2&\cdots&p_1a_M\\ p_2a_1&p_2a_2&\cdots&p_2a_M\\ \vdots&\vdots&\ddots&\vdots\\ p_Ra_1&p_Ra_2&\cdots&p_Ra_M \end{pmatrix}$$

  其中$p_i$表示R个N维行向量，$a_j$表示M个N维列向量

数学推导

假如我们有一组N维向量，现在要将其降到K维（K小于N），那么应该如何选择K个基才能最大程度保留原有的信息？

---

为了便于理解，现以一个具体例子展开，假设数据由五条记录组成，将它们表示成矩阵形式：

$$\begin{pmatrix} 1&1&2&4&2\\ 1&3&3&4&4\\ \end{pmatrix}$$

其中每一列为一条数据记录，每一行代表一个随机变量

为了减小误差以及后续处理的方便，首先将每个字段进行零均值化，即减去字段的平均值，其结果是将每个字段的均值都变为零

$$\begin{pmatrix} -1&-1&0&2&0\\ -2&0&0&1&1\\ \end{pmatrix}$$

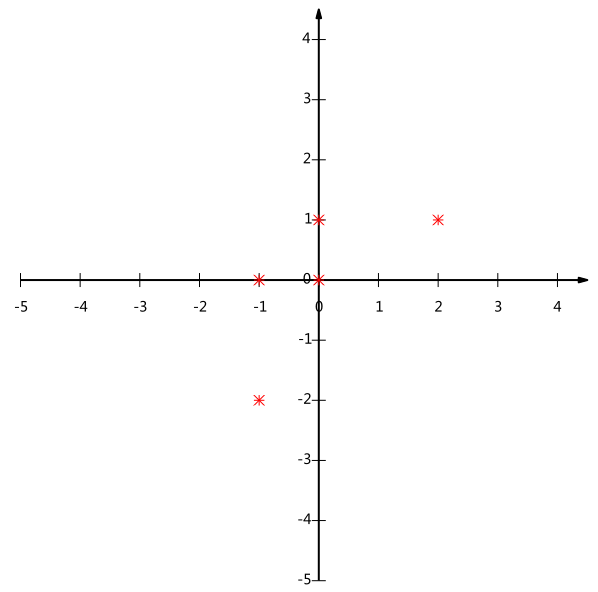
现在五条数据在平面直角坐标系内的表示如下：

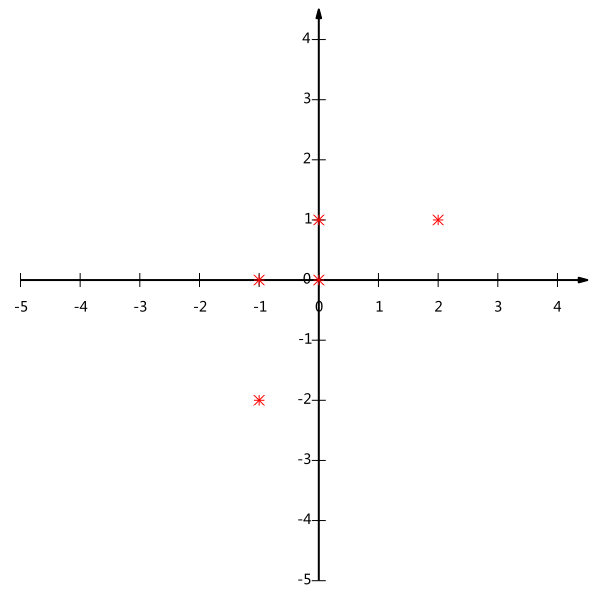
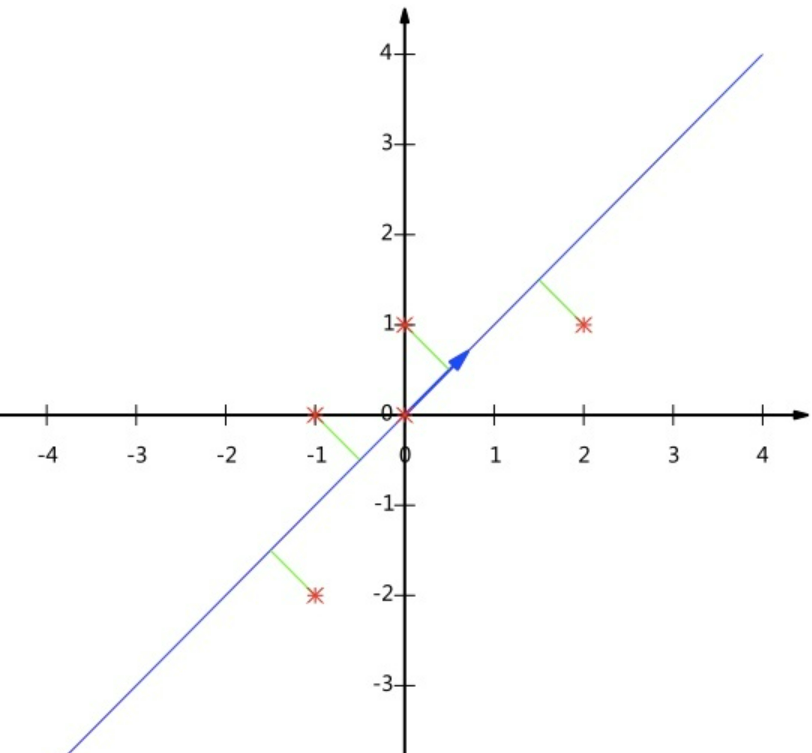
假如我们现在必须使用一维来表示这些数据（降维），又希望尽量保留原始信息——其实质便是在二维平面中选择一个方向，将所有数据都投影到这个方向所在直线上，用投影值表示降维后的数据，并让投影后的投影值尽可能分散

投影值的分散程度可以用数学上的方差来表述：

$$Var(x) = \frac{1}{n}\sum_{i=1}^n(x_i-\bar x)^2$$

由于上面我们已经将每个字段都化为零均值了，故方差可以直接用以下公式表示：

$$Var(x) = \frac{1}{n}\sum_{i=1}^nx_i^2$$

故最终我们是需要寻找一个一维基向量，使得所有数据变换为这个基上的坐标表示后，方差最大

---

对于上面二维降成一维的情况来说，只要找到使得那个方差最大的方向即可。但对于更高维，不仅需要寻找其他的投影方向，还需要让多个字段间尽可能没有相关性

假如要让两个字段尽可能表示更多的原始信息，就意味着让它们之间尽量不存在（线性）相关性，数学上可以用两个字段的协方差表示其相关性，由于已经将每个字段去中心化，则：

$$Cov(X,Y) = \frac{1}{n}\sum_{i=1}^nx_iy_i$$

当协方差为0时，表示两个字段不存在（线性）相关性。为了让协方差为0，我们选择第二个基向量时只能在与第一个基向量正交的方向上选择。因此最终选择的两个方向一定是正交的

故降维的最终目标为：要将一组N维向量降为K维（K小于N），其目标是寻找K个单位正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）

---

由上面的推导过程可知，最终要达到的目标与字段内方差及字段间协方差由密切关系，故可以用数学上的协方差矩阵将两者统一表示

假设现在只有a和b两个字段，将它们按行组成矩阵$X$：

$$X = \begin{pmatrix} a_1&a_2&...&a_n\\ b_1&b_2&...&b_n\\ \end{pmatrix}$$

则$X$的协方差矩阵为：

$$C = \frac{1}{n}XX^T = \begin{pmatrix} \frac{1}{n}\sum_{i=1}^na_i^2&\frac{1}{n}\sum_{i=1}^na_ib_i\\ \frac{1}{n}\sum_{i=1}^na_ib_i&\frac{1}{n}\sum_{i=1}^nb_i^2\\ \end{pmatrix}$$

可以发现，主对角线上两个元素分别是两个字段的方差，而其它元素是a和b的协方差，两者被统一到了一个矩阵中

根据矩阵相乘的运算法则，上述结论可以推广到一般情况：设有m条n维数据记录，将其按列排成n行m列的矩阵$X$，设$C = \frac{1}{n}XX^T$，则$C$是一个对称矩阵，其主对角线上的元素分别为各个字段的方差，而第$i$行$j$列与第$j$行$i$列的元素相同，表示$i$和$j$两个字段的协方差

根据上述推导可以得知，要达到降维的最终目标，等价于将协方差矩阵对角化：即除主对角线外的其它元素化为0，并在主对角线上将元素按从大到小的顺序从上到下排列

---

现在进一步来看一下原矩阵的协方差矩阵与降维后矩阵的协方差矩阵的关系。设原始数据矩阵$X$对应的协方差矩阵为$C$，而$P$是一组基向量按行组成的矩阵。设$Y=PX$，则$Y$为$P$对$X$做基变换后的数据。设$Y$的协方差矩阵为$D$，可得：

$$\begin{aligned} D&= \frac{1}{n}YY^T \\ &= \frac{1}{n}(PX)(PX)^T \\ &= \frac{1}{n}PXX^TP^T \\ &= P(\frac{1}{n}XX^T)P^T \\ &= PCP^T \end{aligned}$$

至此我们可以得出结论：寻找一个矩阵$P$（正交变换），满足$PCP^T$是一个对角矩阵，并且对角线元素按从大到小的次序排列，则$P$的前K行就是要寻找的基向量，用$P$的前K行组成的矩阵乘以$X$使得$X$从N维降到了K维并最大程度保留了原有信息

最小实例

以$X$为例，使用PCA将这两行数据降到一行

$X = \begin{pmatrix} -1&-1&0&2&0\\ -2&0&0&1&1\\ \end{pmatrix}$

因为$X$矩阵的每行已经是零均值，所以不需要去平均值

求协方差矩阵：

$C = \frac{1}{5}\begin{pmatrix} -1&-1&0&2&0\\ -2&0&0&1&1\\ \end{pmatrix} \begin{pmatrix} -1&-2\\ -1&0\\ 0&0\\ 2&1\\ 0&1\\ \end{pmatrix} = \begin{pmatrix} \frac{6}{5}&\frac{4}{5}\\ \frac{4}{5}&\frac{6}{5}\\ \end{pmatrix}$

求协方差矩阵的特征值与特征向量：

$\lambda_1 = 2，\lambda_2 = \frac{2}{5}$

$c_1 = \begin{pmatrix} 1\\ 1\\ \end{pmatrix} ，c_2 = \begin{pmatrix} -1\\ 1\\ \end{pmatrix}$

将特征向量正交单位化：

$p_1 = \begin{pmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\\ \end{pmatrix} ，p_2 = \begin{pmatrix} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\\ \end{pmatrix}$

得到矩阵$P$为：

$P = \begin{pmatrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\ -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\ \end{pmatrix}$

最后用$P$的第一行乘以数据矩阵$X$，就得到了降维后的表示：

$Y = \begin{pmatrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \end{pmatrix} \begin{pmatrix} -1&-1&0&2&0\\ -2&0&0&1&1\\ \end{pmatrix} = \begin{pmatrix} -\frac{3}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0&\frac{3}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \end{pmatrix}$

总结

PCA算法实际步骤：

设有m条n维数据，

1. 将原始数据按列组成n行m列的矩阵$X$
2. 将$X$的每一行进行零均值化，即减去这一行的均值
3. 求出协方差矩阵 $C = \frac{1}{n}XX^T$
4. 求出协方差矩阵的特征值和特征向量，并将特征向量正交单位化
5. 对特征值从大到小排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为行向量组成矩阵P
6. $Y=PX$即为降到k维后的数据

---

如果您觉得阅读本文对您有帮助，请点一下“推荐”按钮，您的“推荐”将是我最大的写作动力！欢迎各位转载，但是未经作者本人同意，转载文章之后必须在文章页面明显位置给出作者和原文连接，否则保留追究法律责任的权利。