轮廓拟合

轮廓拟合

简介

• 由于噪声和光照的影响，物体的轮廓会出现不规则的形状，不规则的轮廓形状不利于对图像内容进行分析，此时需要将物体的轮廓拟合成规则的几何形状，根据需求可以将图像轮廓拟合成矩形、多边形等

---

矩形

最大外接矩形

Rect cv::boundingRect(IuputArray array)

• array：输入的灰度图像或者二维点集，灰度图像的参数类型为 Mat，二维点集的参数类型为 vector 或者 Mat

该函数的返回值是一个 Rect 类型的变量，该变量可以直接用rectangle()函数绘制矩形

最小外接矩形

RotatedRect cv::minAreaRect(IuputArray points)

• points：表示输入的二维点集合

返回值是 RotatedRect 类型的变量，含有矩形的中心位置，矩形的宽和高，以及矩形旋转的角度。RotatedRect 类具有两个重要的方法和属性，可以输出矩形的4个顶点和中心坐标。输出4个顶点坐标的方法是 points()。假设 RotatedRect 类的变量为 rrect，可以通过rrect.points(points)命令进行读取，其中存放坐标的变量是 Point2f 类型的数组。输出矩形中心坐标的属性是 center，假设 RotatedRect 类的变量 rrect，可以通过opt = rrect.center命令进行读取，其中存放坐标的变量是 Point2f 类型

---

圆

void cv::minEnclosingCircle(IuputArray points, Point2f & center, float & radius)

• points：待寻找包围圆形的二维点集，类型为 vector<Point> 或者 Mat
• center：圆形的圆心
• radius：圆形的半径

---

三角形

double cv::minEnclosingTriangle(InputArray points, OutputArray, triangle)

• points：待寻找包围三角形的二维点集，类型为 vector<Point>
• triangle：拟合出的三角形的3个顶点坐标，存放在 vector<Point2f> 类型的变量中

该函数能够找到包含给定三维点集的最小区域的三角形，返回值为 double 类型的三角形面积

---

实现

示例代码：

#include <opencv2/opencv.hpp>
#include <vector>
using namespace cv;
using namespace std;
 
int main()
{
    Mat img = imread("/home/kslas/test.jpg");
    Mat img1, img2, img3, img4;
    img.copyTo(img1);   // 深拷贝用来绘制最大外接矩形
    img.copyTo(img2);   // 深拷贝用来绘制最小外接矩形
    img.copyTo(img3);   // 深拷贝用来绘制拟合三角形
    img.copyTo(img4);   // 深拷贝用来绘制拟合圆形
    imshow("img", img);
 
    // 去噪声与二值化
    Mat canny;
    Canny(img, canny, 80, 160, 3, false);
    imshow(" ", canny);
 
    // 膨胀运算，将细小缝隙填补
    Mat kernel = getStructuringElement(0, Size(3, 3));
    dilate(canny, canny, kernel);
 
    // 轮廓的发现与绘制
    vector<vector<Point>> contours;
    vector<Vec4i> hierarchy;
    findContours(canny, contours, hierarchy, 0, 2);
 
    // 寻找轮廓拟合图形
    for (int i = 0; i < contours.size(); i++)
    {
        // 最大外接矩形
        Rect rect = boundingRect(contours[i]);
        rectangle(img1, rect, Scalar(0, 0, 255), 2);
 
        // 最小外接矩形
        RotatedRect rrect = minAreaRect(contours[i]);
        Point2f points[4];
        rrect.points(points);   // 读取最小矩形的4个顶点
        Point2f cpt = rrect.center;   // 最小外接矩形的中心
        // 绘制旋转矩形与中心位置
        for (int j = 0; j < 4; j++)
        {
            if (j == 3)
            {
                line(img2, points[j], points[0], Scalar(0, 255, 0), 2);
                break;
            }
            line(img2, points[j], points[j + 1], Scalar(0, 255, 0), 2);
        }
        // 绘制矩形的中心
        circle(img, cpt, 2, Scalar(255, 0, 0), 2);
 
        // 绘制三角形
        vector<Point> triangle;
        double area = minEnclosingTriangle(contours[i], triangle);
        for (int j = 0; j < 3; j++)
        {
            if (j == 2)
            {
                line(img3, triangle[j], triangle[0], Scalar(255, 0, 0), 2);
                break;
            }
            line(img3, triangle[j], triangle[j + 1], Scalar(255, 0, 0), 2);
        }
 
        // 绘制圆形
        Point2f center;
        float radius = 0;
        minEnclosingCircle(contours[i], center, radius);
        circle(img4, center, cvRound(radius), Scalar(0, 0, 0), 2);
    }
 
    // 输出轮廓拟合结果
    imshow("max_rect", img1);
    imshow("min_rect", img2);
    imshow("triangle", img3);
    imshow("circle", img4);
    waitKey(0);
    destroyAllWindows();
    return 0;
}

运行结果：

---

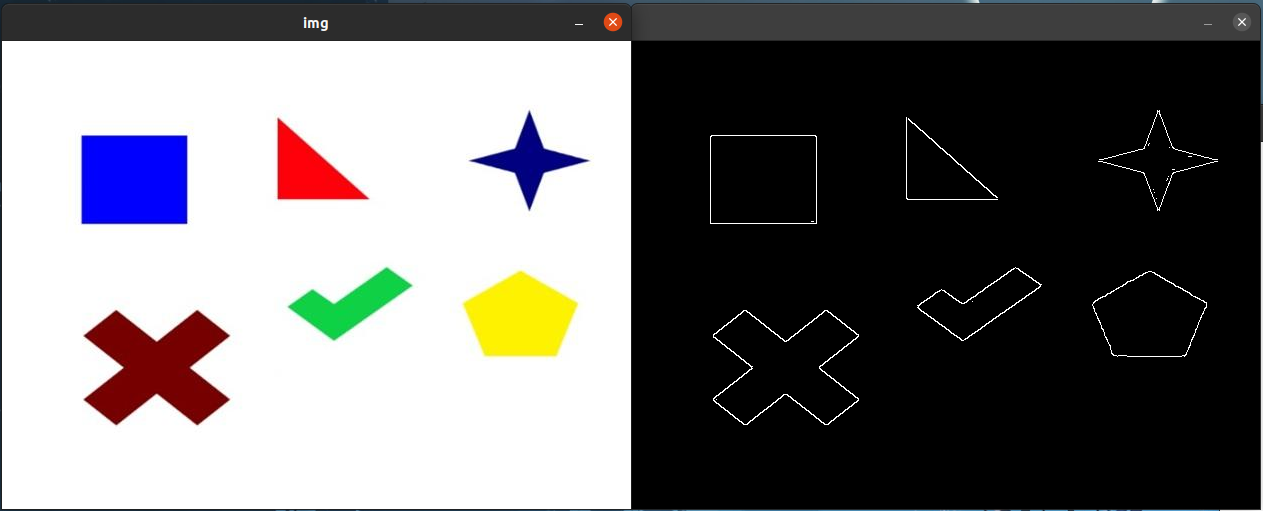
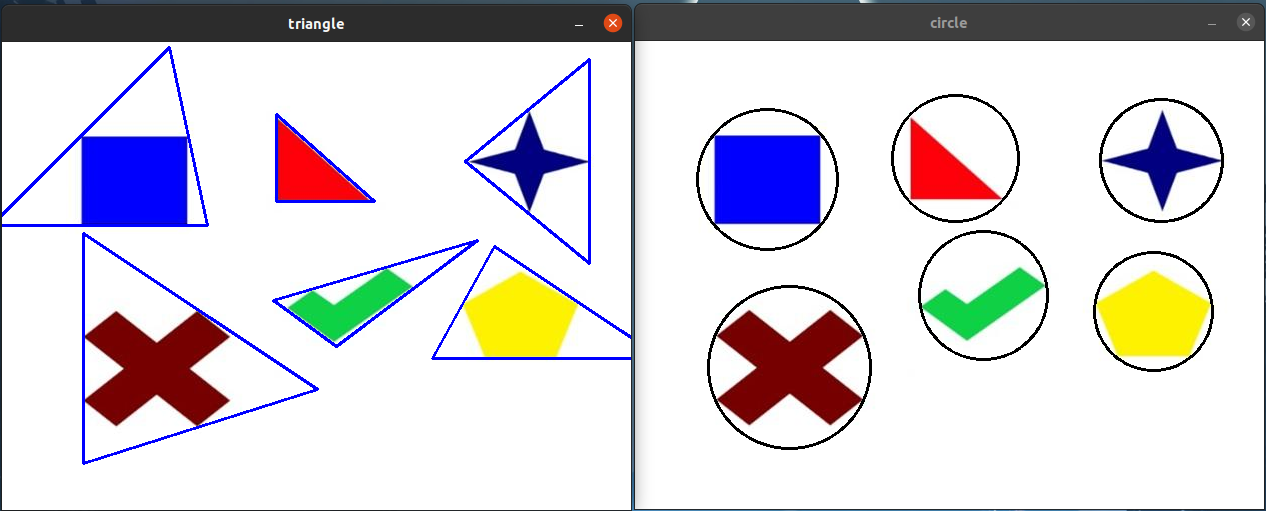
如果您觉得阅读本文对您有帮助，请点一下“推荐”按钮，您的“推荐”将是我最大的写作动力！欢迎各位转载，但是未经作者本人同意，转载文章之后必须在文章页面明显位置给出作者和原文连接，否则保留追究法律责任的权利。