附注2-非方阵
在这个小测验里，我让你们求一个2x3矩阵的行列式。
让我感到非常可笑的是，你们当中竟然有人尝试去做。
——摘自mathprofessorquotes.com，作者佚名
- 讨论不同维数之间的变换是完全合理的，比如一个二维向量到三维向量的变换
-
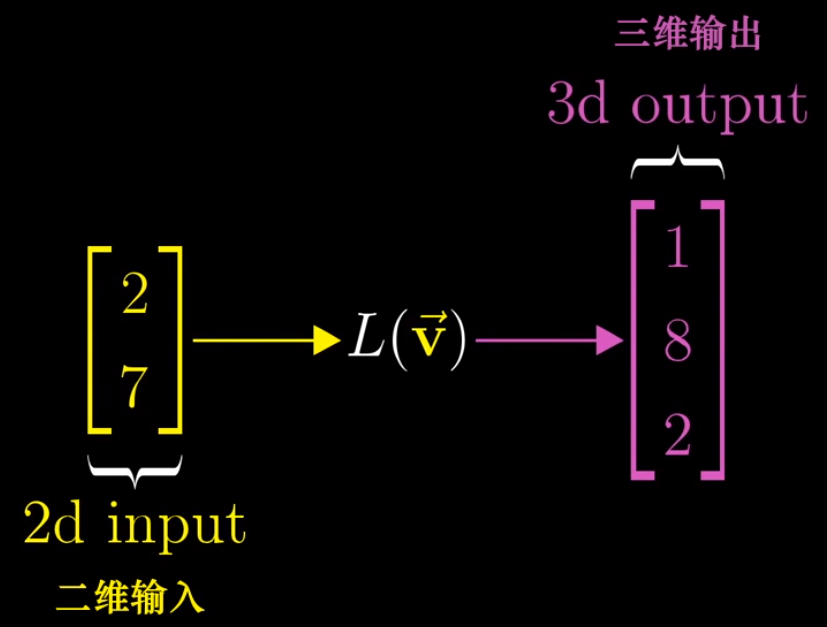
同之前一样，如果网格线保持平行且等距分布，并且原点映射为自身，就称它是线性的
-
这里所展示的，左侧为输入空间，也就是二维空间，右侧为输出空间，也就是变换后的空间
-
值得强调一点，输入的二维向量与输出的三维向量是完全不同的 “物种” ，它们生活在没有任何关联的空间当中
-
用矩阵代表这样一个变换则和之前的方法相同，找到每一个基向量变换后的位置，然后把变换后基向量的坐标作为矩阵的列
-
比如说，现在看到的是一个变换后的空间，这个变换将i帽变换到坐标（2，-1，-2），j帽变换到坐标（0，1，1）
-
注意一点，这意味着代表这个变换的矩阵是三行两列的，用术语来说，这是一个3x2矩阵
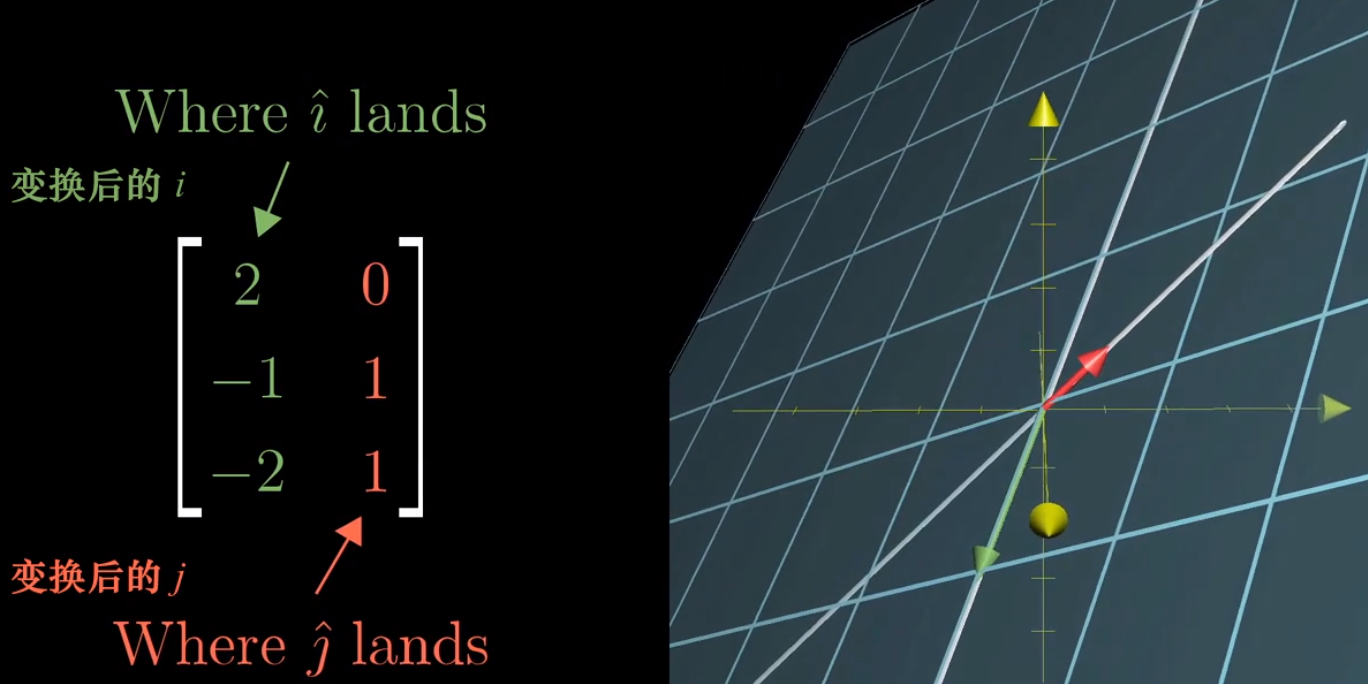
- 这个矩阵的列空间，是三维空间中一个过原点的二维平面。但是这个矩阵仍然是满秩的，因为列空间的维数与输入空间的维数相等
- 所以当你看到一个3x2矩阵的时候，你就会明白它的几何意义是将二维空间映射到三维空间上。因为矩阵有两列表明输入空间有两个基向量，有三行表明每一个基向量在变换后都用三个独立的坐标来描述
\[\left[
\begin{matrix}
3 & 1 \\
4 & 1 \\
5 & 9
\end{matrix}
\right] \
\]
- 类似的，当你看到一个两行三列的2x3矩阵时，你觉得它代表什么？
\[\left[
\begin{matrix}
3 & 1 & 4 \\
1 & 5 & 9
\end{matrix}
\right] \
\]
-
矩阵有三列表明原始空间有三个基向量，也就是说原始空间是三维的。有两行表明这三个基向量在变换后都仅用两个坐标来描述
-
所以它们一定落在二维空间中，因此这是一个从三维空间到二维空间的变换
-
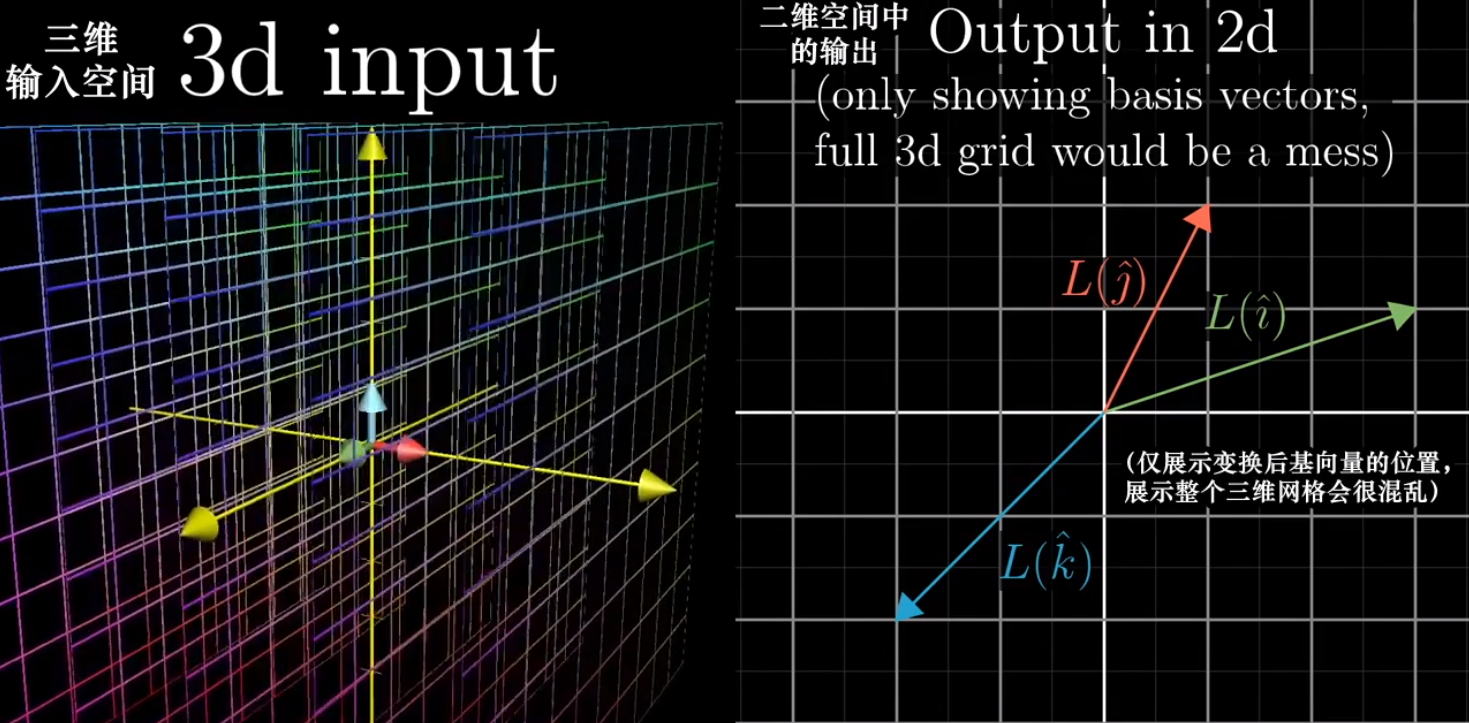
你还可以有二维空间到一维空间的变换
-
一维空间实际上就是数轴。所以这样的变换接收二维向量，然后产生一个数
-
因为空间的挤压，在这里考虑网格线保持平行且等距分布显得有些混乱，所以在这种情况下，形象理解线性性质的含义就是说：如果在一条直线上有一系列等距分布的点，在映射到数轴之后，它们将保持等距分布
- 这样的变换由一个1x2矩阵表示，而这个矩阵的两列都只有一个数，这两列分别代表了变换后的基向量，而它们都只需要一个数字，即变换后基向量在数轴上的位置
