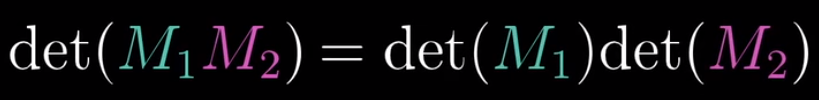05-行列式
计算的目的不在于数字本身,
而在于洞察其背后的意义。
—理查德‧哈明
行列式
二维空间
-
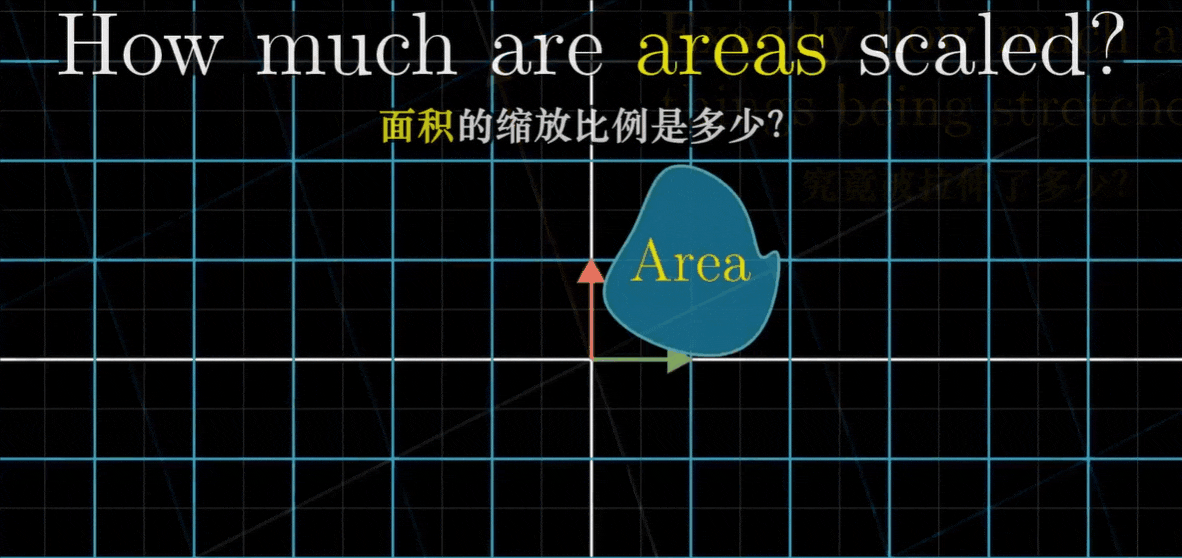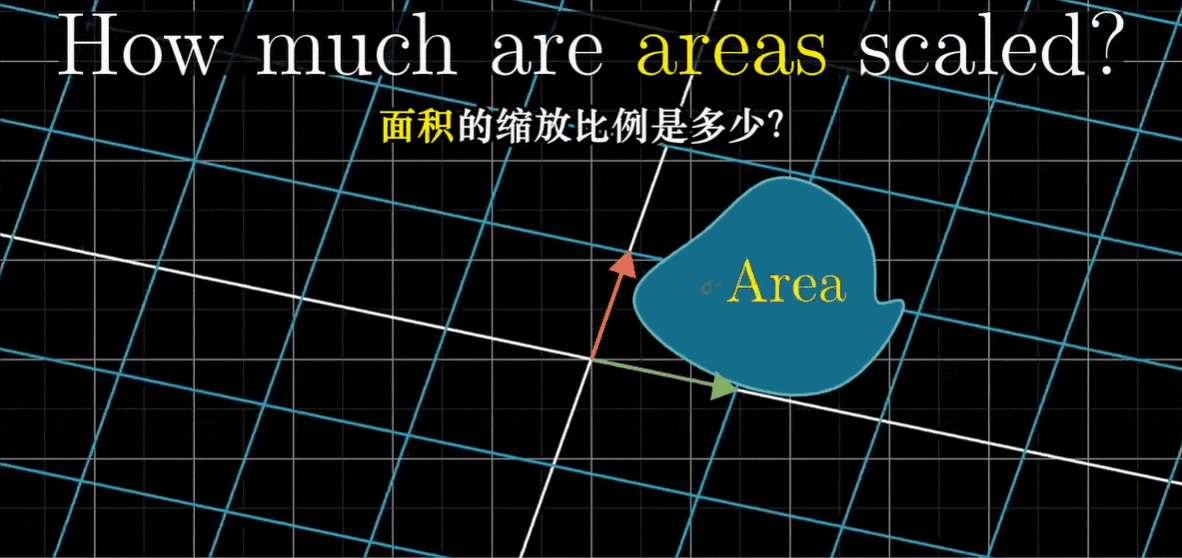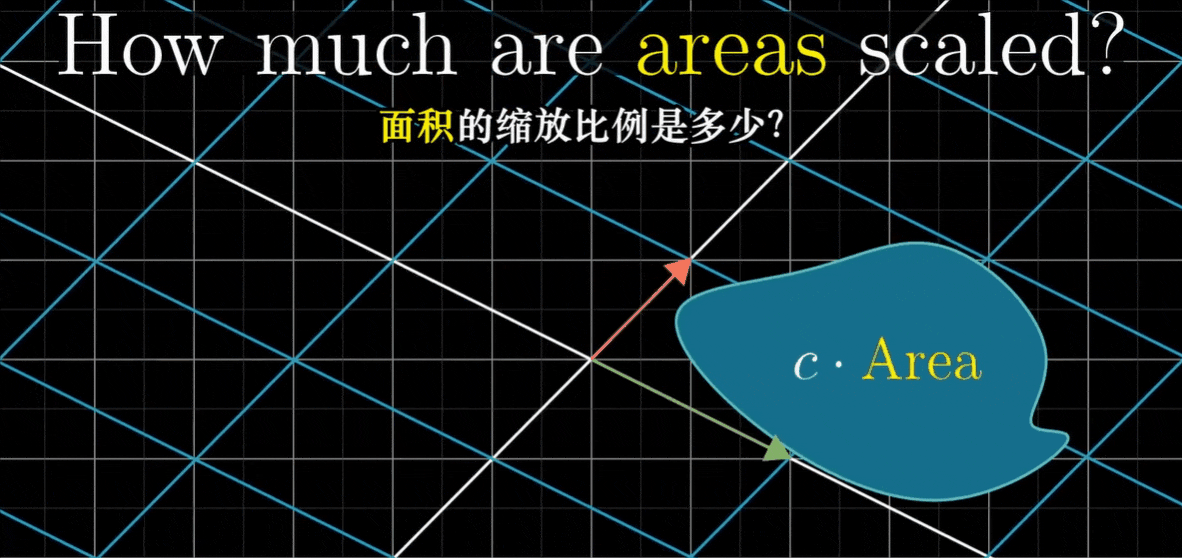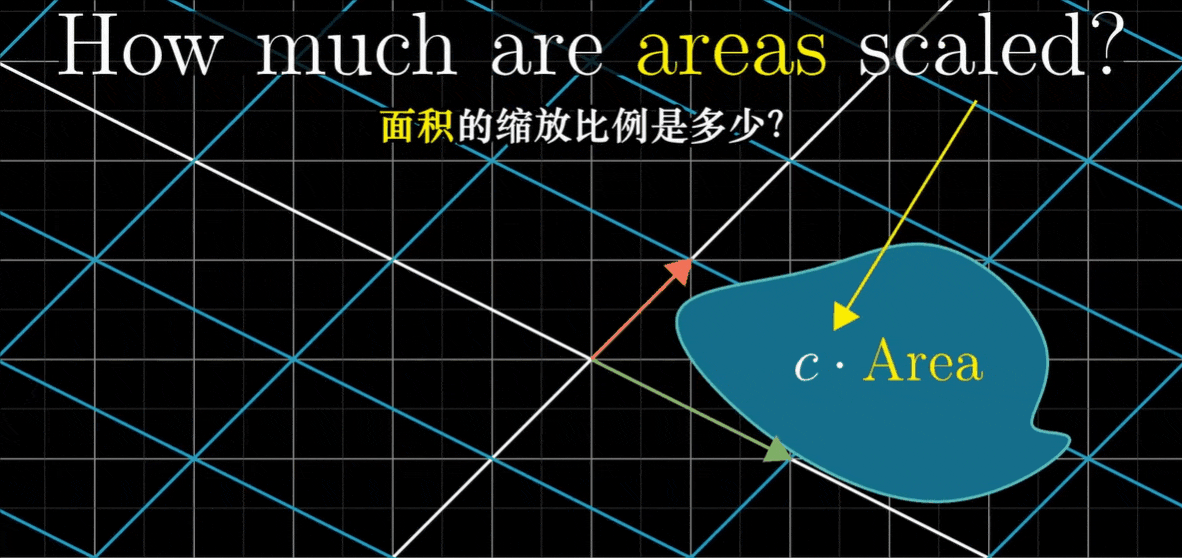
现在想象一些线性变换,你可能注意到其中有的将空间向外拉伸,有的则将空间向内挤压
-
有件事对理解这些线性变换很有用,那就是测量变换究竟对空间有多少拉伸或挤压。更具体一点,就是测量一个给定区域面积增大或减小的比例
-
比如说这样一个以(3,0)和(0,2)为列的矩阵,它将i帽伸长为原来的3倍,将j帽伸长为原来的2倍
-
现在如果我们关注以i帽为底边,以j帽为左边的 1x1 正方形,在变换之后,它会变成一个 2x3 矩形
-
因为这个区域初始面积为1,最终面积为6,所以我们说这个线性变换将它的面积变为6倍

- 剪切矩阵的列为(1,0)和(1,1),也就是说i帽保持不变,而j帽移动至(1,1)。由i帽和j帽决定的单位正方形在变换后倾斜为一个平行四边形,但这个平行四边形的面积仍旧为1,因为它的底和高的长度还是1。所以说,即便这个变换将空间向右挤压,至少对于这个单位正方形来说,它似乎并不改变面积

-
实际上,你只要知道这个单位正方形面积变化的比例,它就能告诉你其他任意区域的面积变化比例
-
首先需要注意一点,无论一个方格如何变化,对其他大小的方格来说,都会有相同的变化,这是由 “网格线保持平行且等距分布” 这一事实推断出的
-
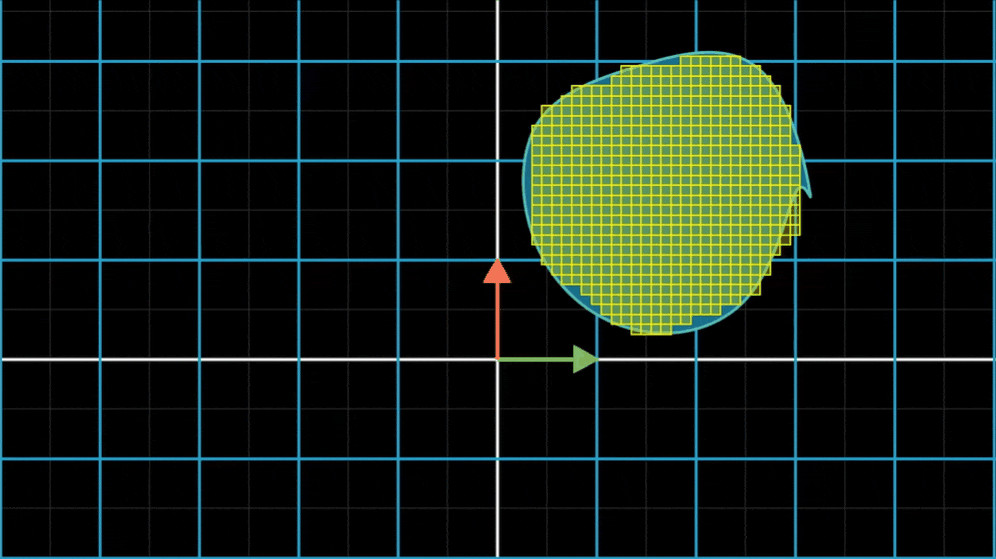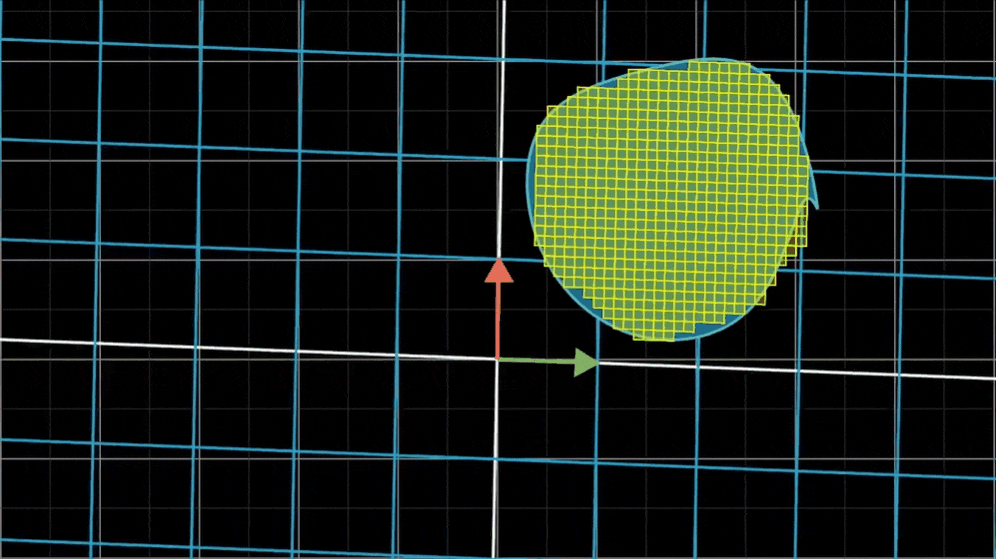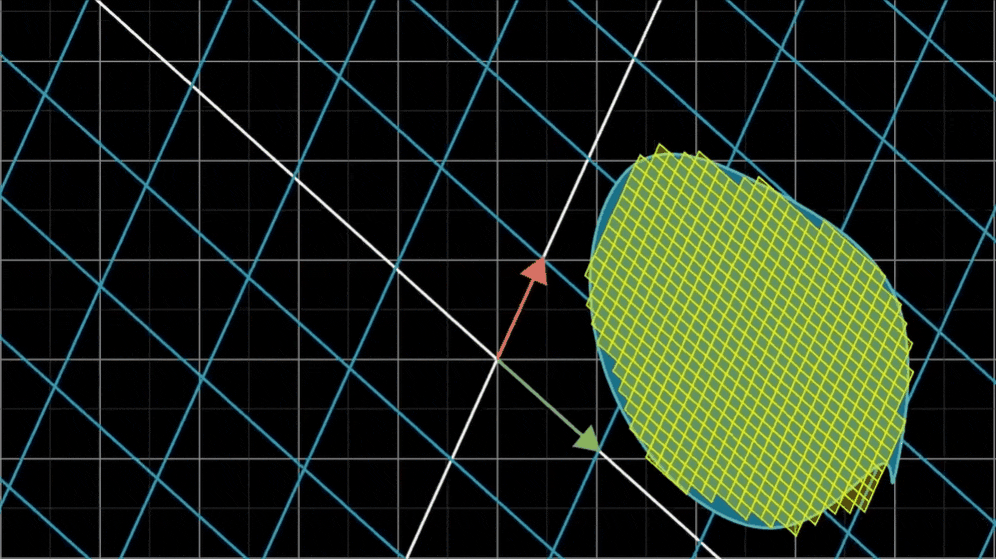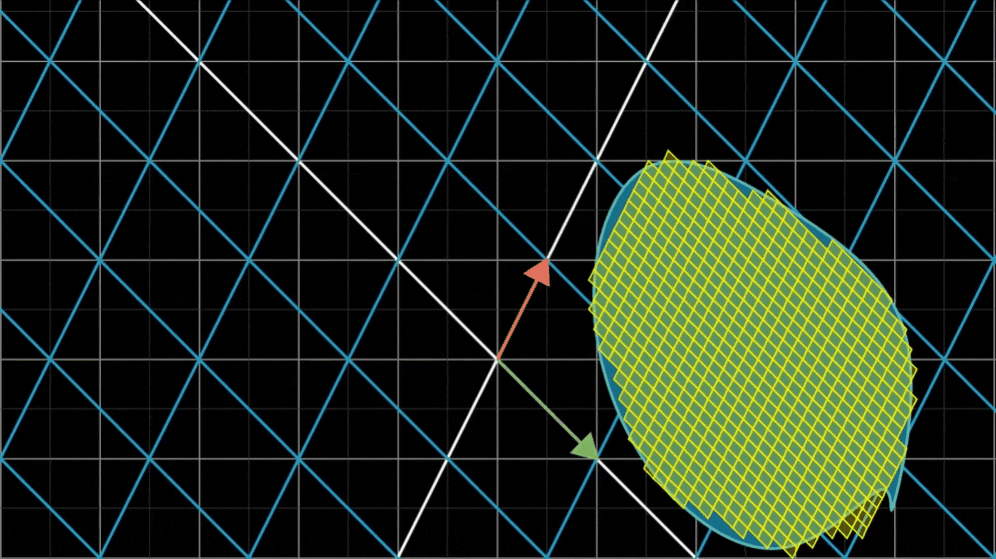
对于不是方格的形状,它们可以用许多方格良好近似。只要使用的方格足够小,近似就能足够好
-
由于所有小方格都进行了一个比例的缩放,所以整个形状也进行了同样比例的缩放
-
这个特殊的缩放比例,即线性变换改变面积的比例,被称为这个变换的行列式
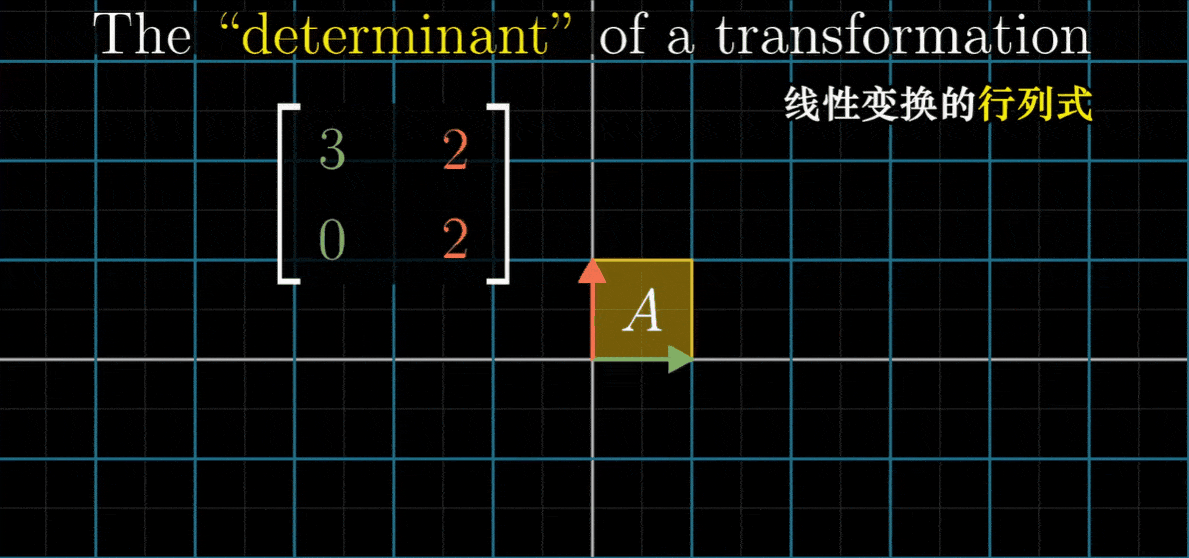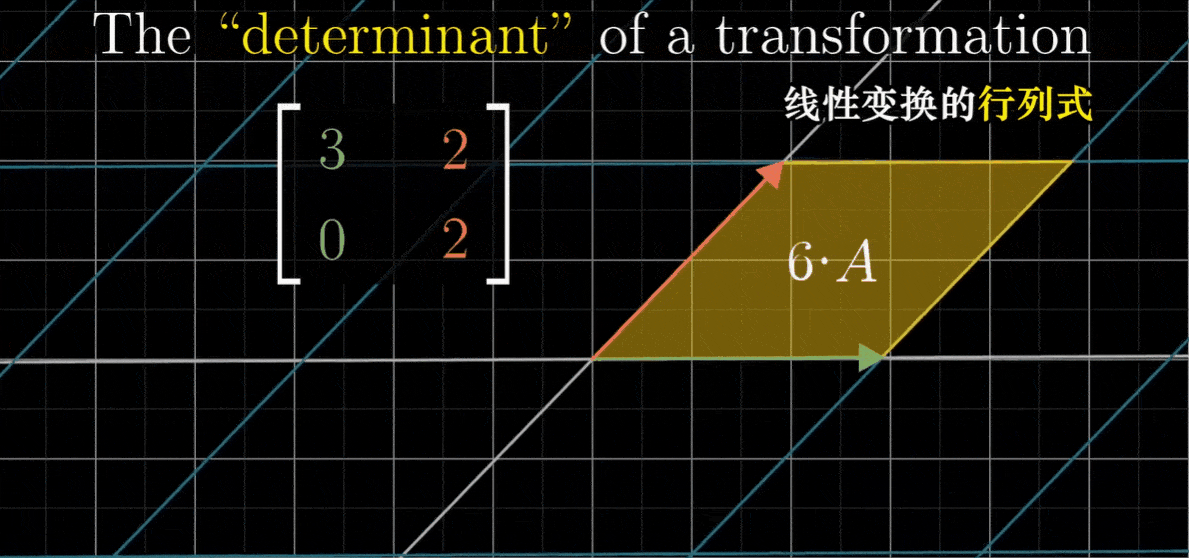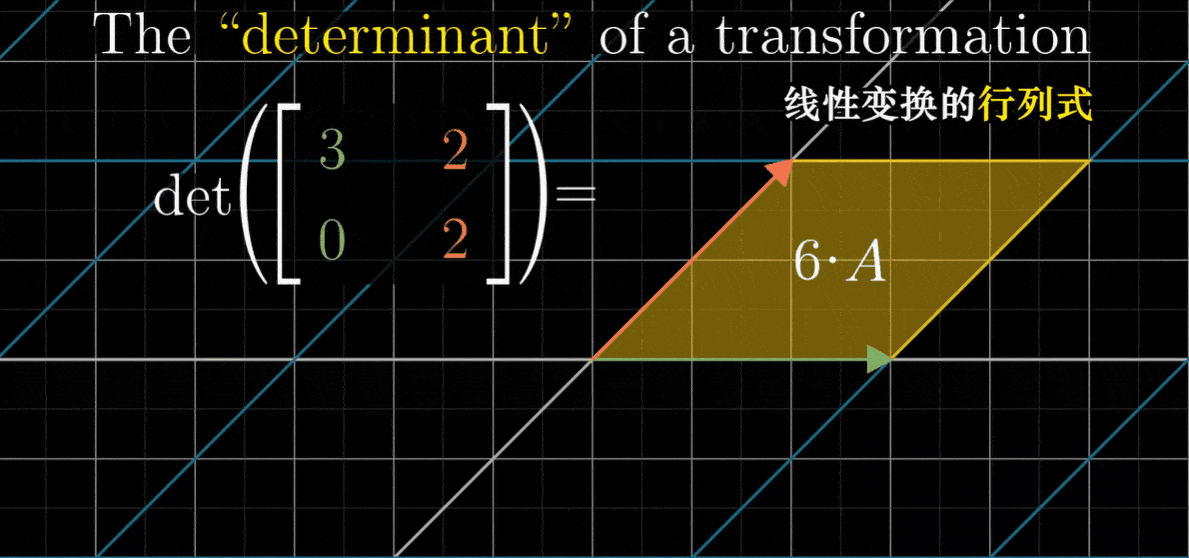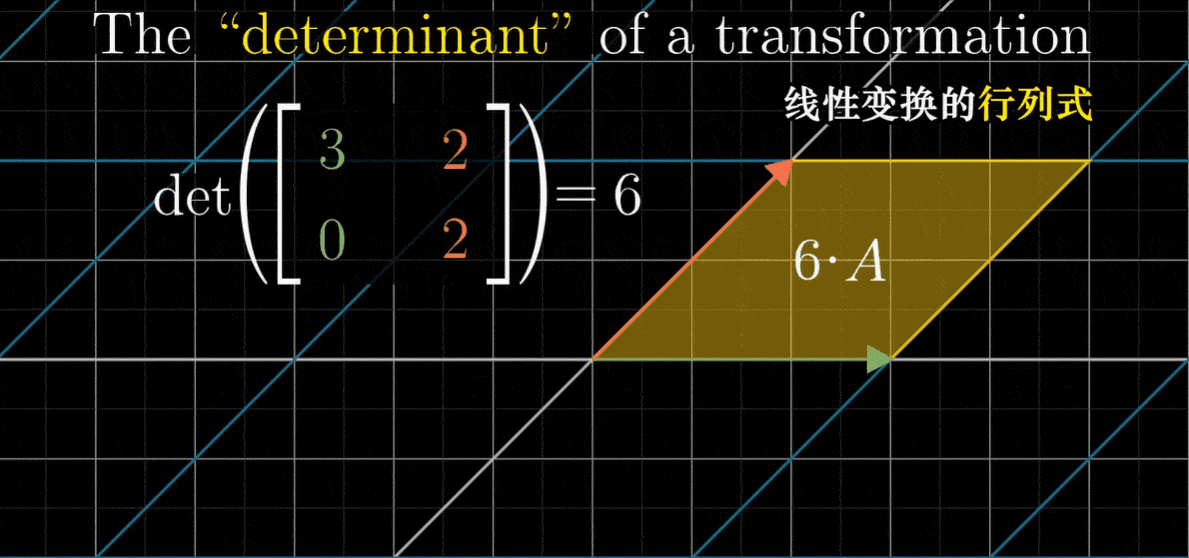
- 比如说,一个线性变换的行列式是3,就是说它将一个区域的面积增加为原来的3倍

- 一个线性变换的行列式是1/2,就是说它将一个区域的面积缩小一半

- 而一个二维线性变换的行列式为0,说明它将整个平面压缩到一条线、甚至是一个点上,因为此时任何区域的面积都变成了0
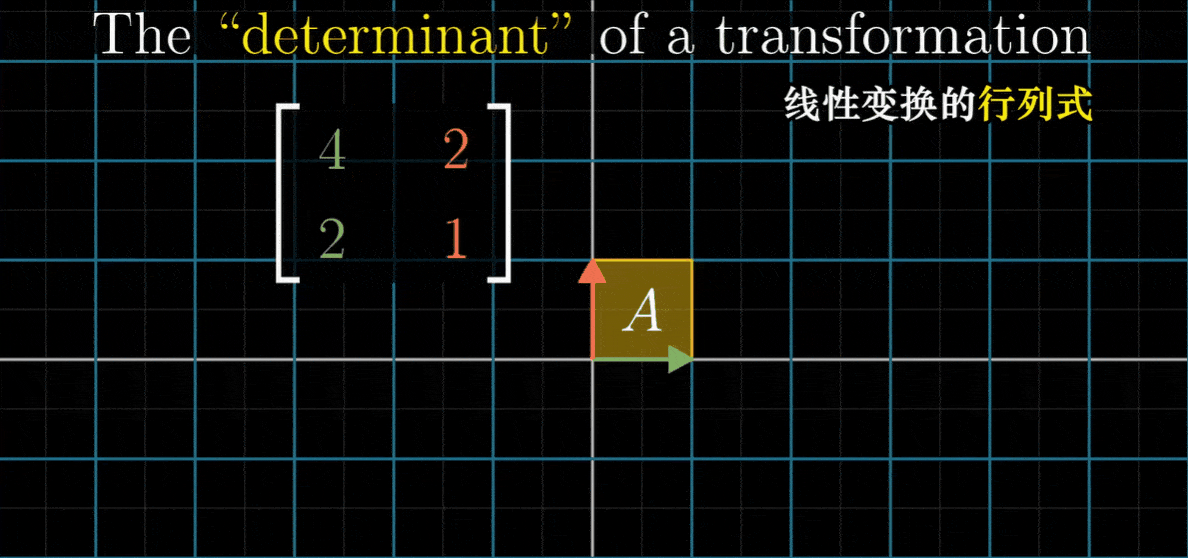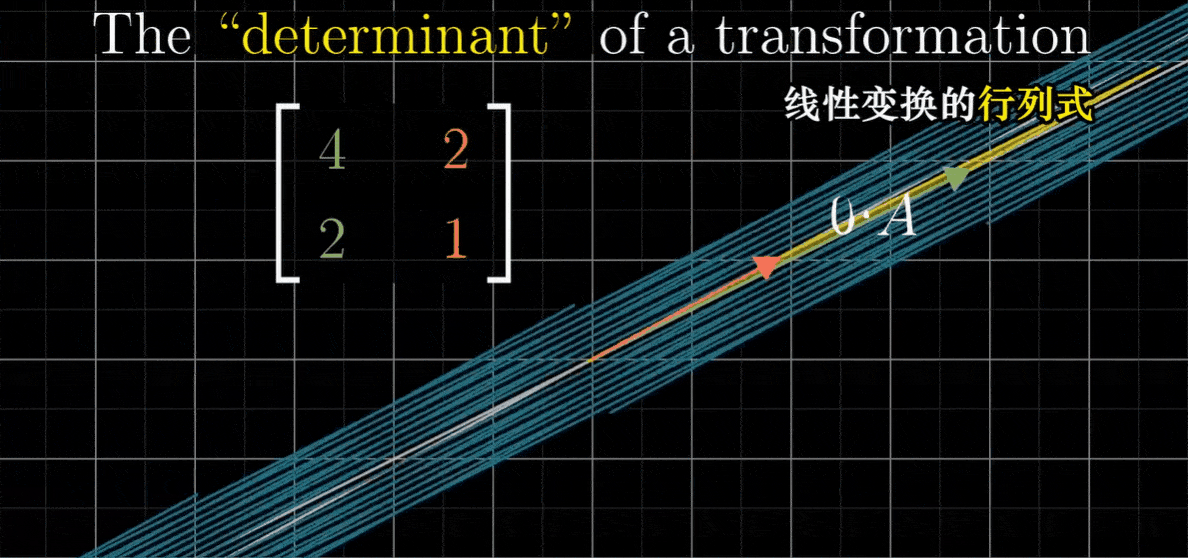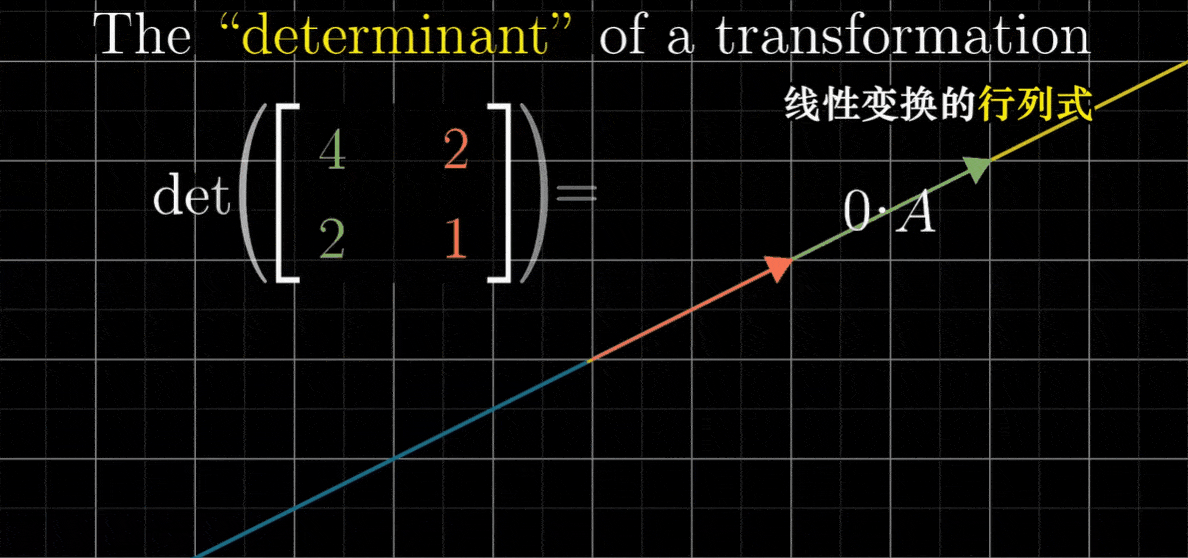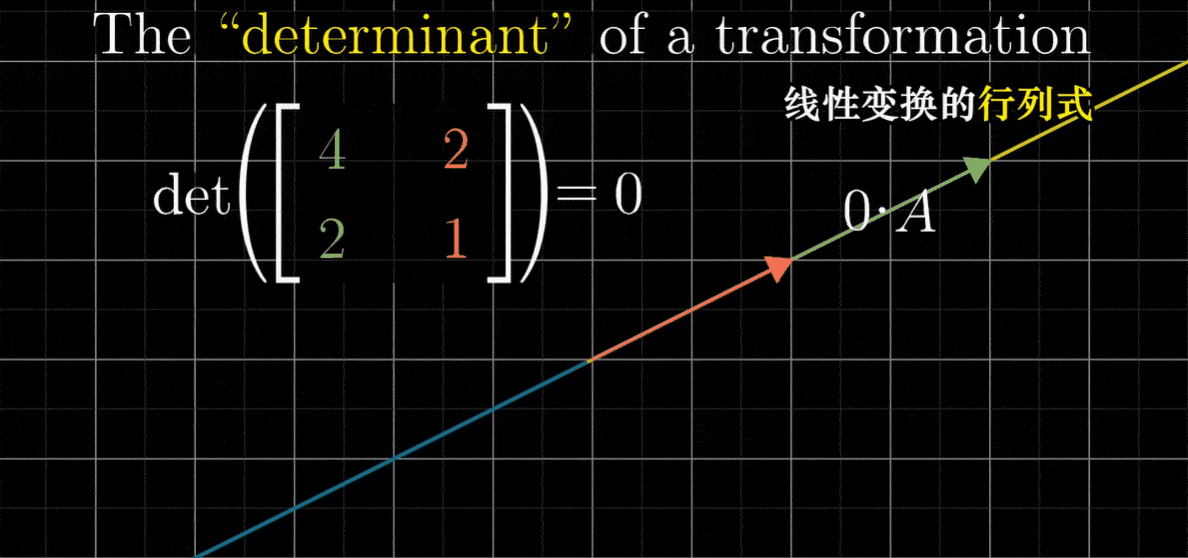
- 最后这个例子相当重要,这是说,只需要检验一个矩阵的行列式是否为0,我们就能了解这个矩阵所代表的变换是否将空间压缩到更小的维度上
-
完整概念下的行列式是允许出现负值的,那将一个区域缩放负倍数到底是什么意思?这和定向的概念有关
-
举个例子,注意这个变换在感觉上将整个平面翻转了。如果将二维空间想象为一张纸,这个变换像是将纸翻转到了另一面。我们称类似这样的变换改变了空间的定向

-
另一种方式是根据i帽和j帽来考虑,注意在初始状态时,j帽在i帽的左边。如果在变换之后,j帽处于i帽的右边,那么空间定向就发生了改变
-
当空间定向改变的情况发生时,行列式为负,但是行列式的绝对值依然表示区域面积的缩放比例
-
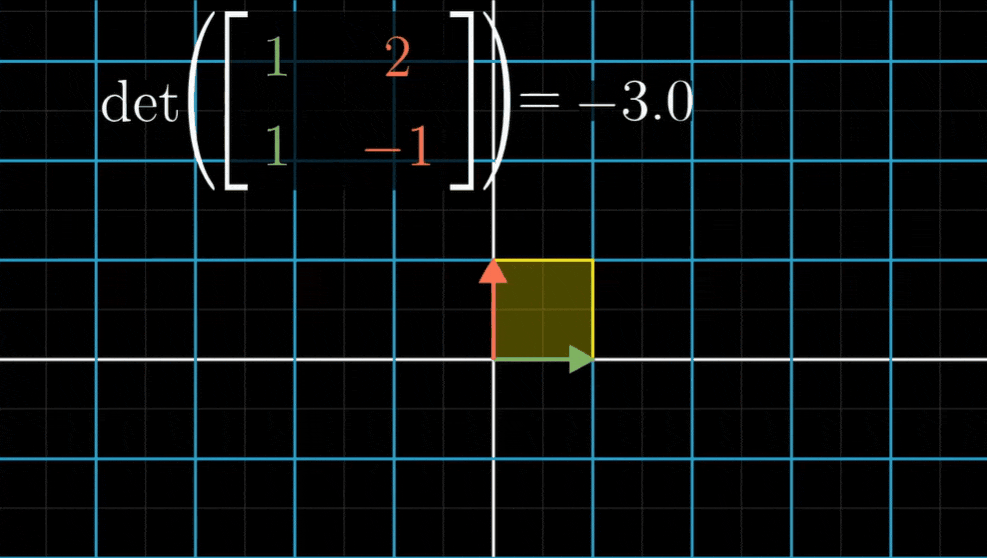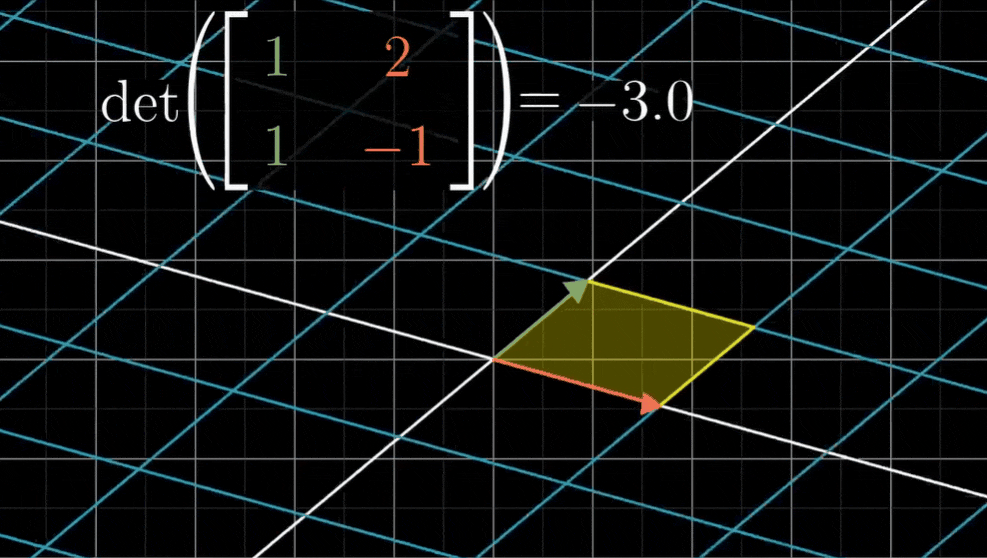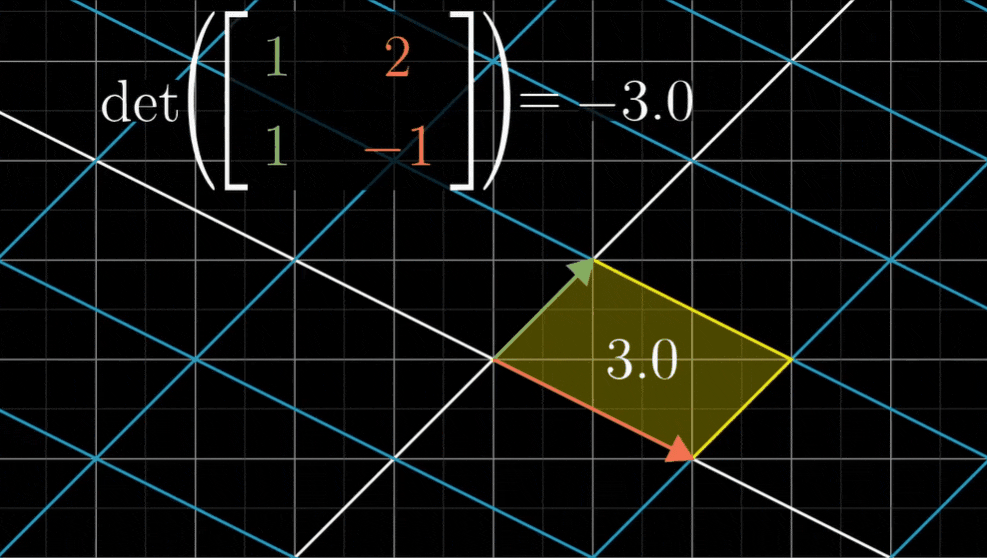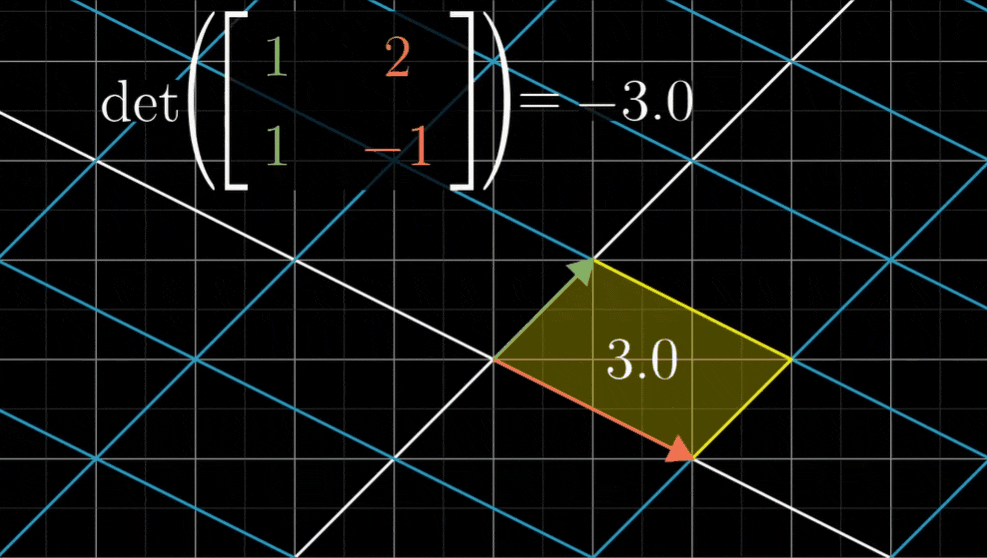
比如说,以(1,1)和(2,-1)为列的矩阵所代表的线性变换的行列式是-3,这就是说变换后空间被翻转,并且面积放大为原来的3倍
三维空间
-
行列式在三维空间中告诉你的依然是变换前后的缩放比例,不过这次它说的是体积的缩放
-
二维空间中,我们最容易考虑一个面积为1的特殊正方形,并观察变换对它的影响
-
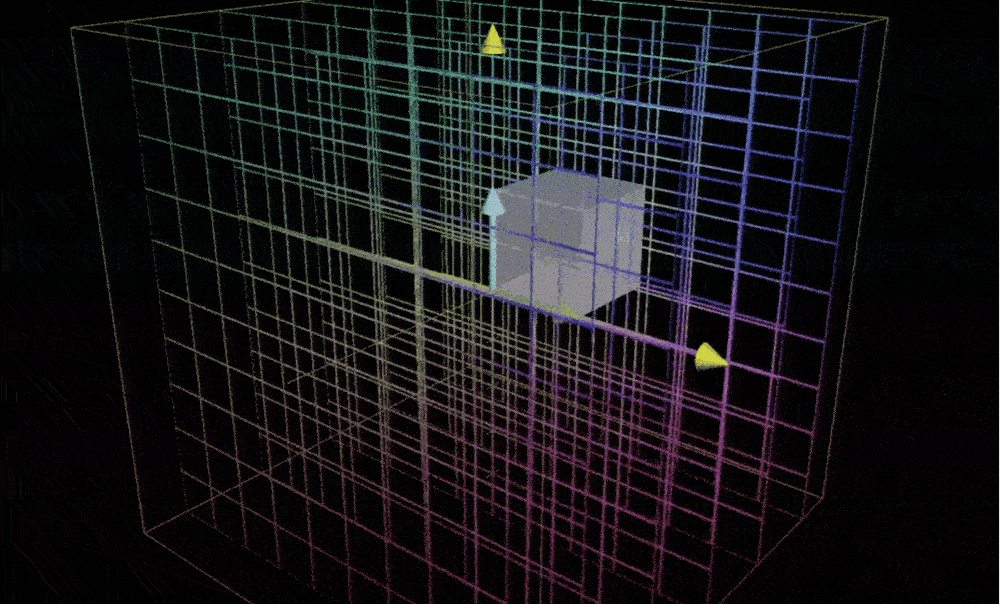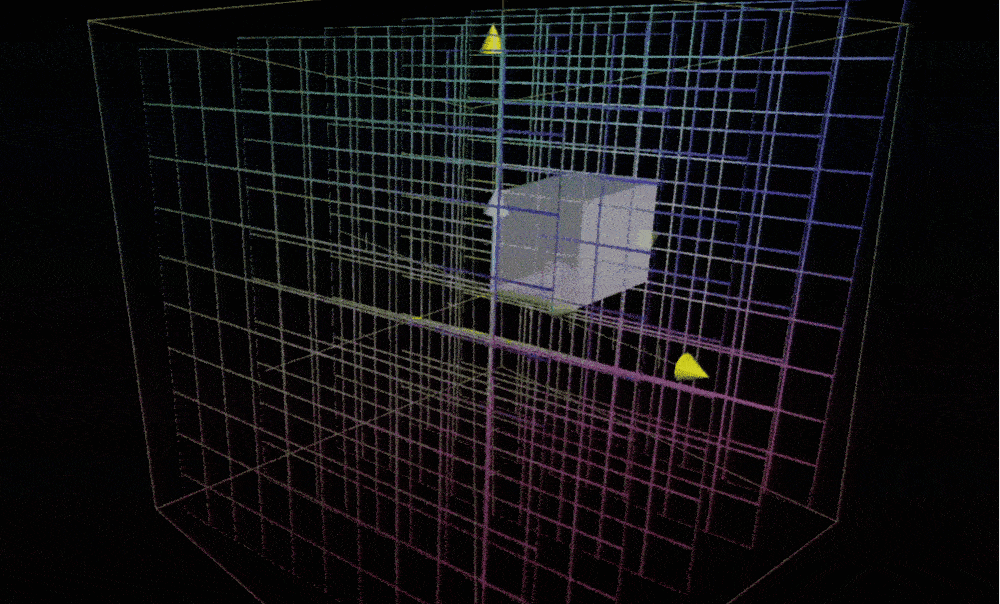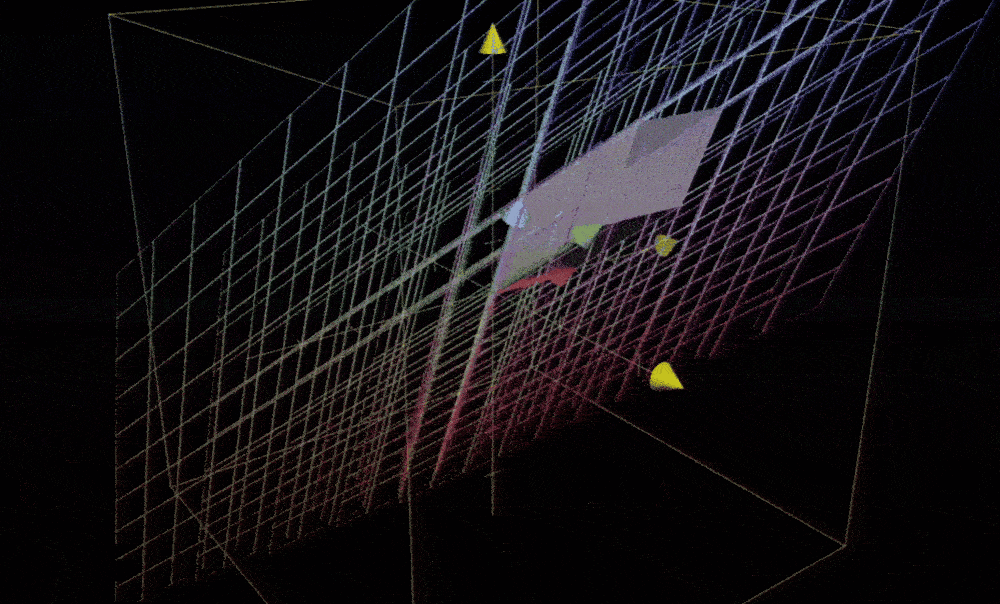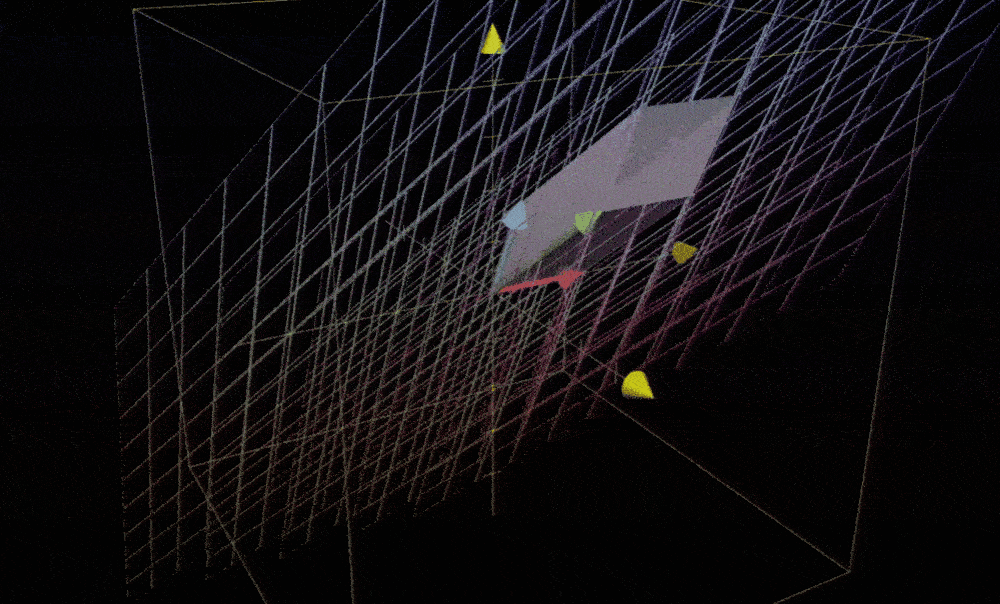
在三维空间中,你聚焦于一个特定的 1x1x1 立方体,它的棱处于基向量i帽、j帽和k帽上。在变换后,这个立方体可能就变成了一个斜不拉几的形状。顺便一提,这个形状有个好听的名字—平行六面体
-
因为这个立方体的初始体积为1,而行列式给出的是体积缩放比例,所以可以把行列式简单看作这个平行六面体的体积
-
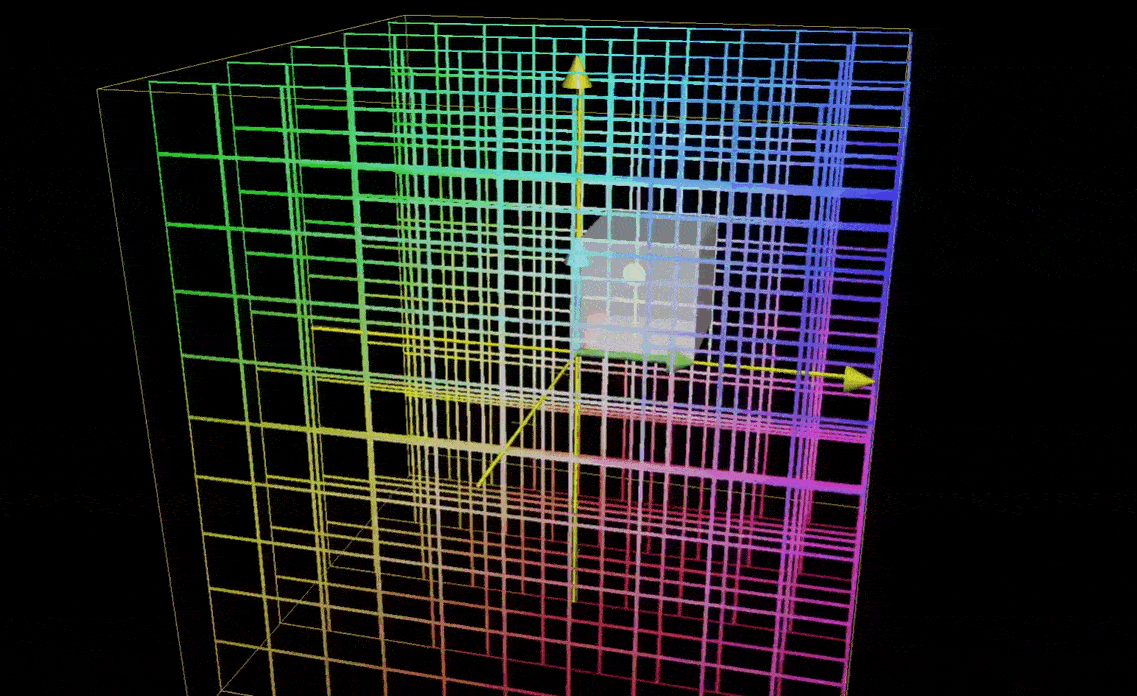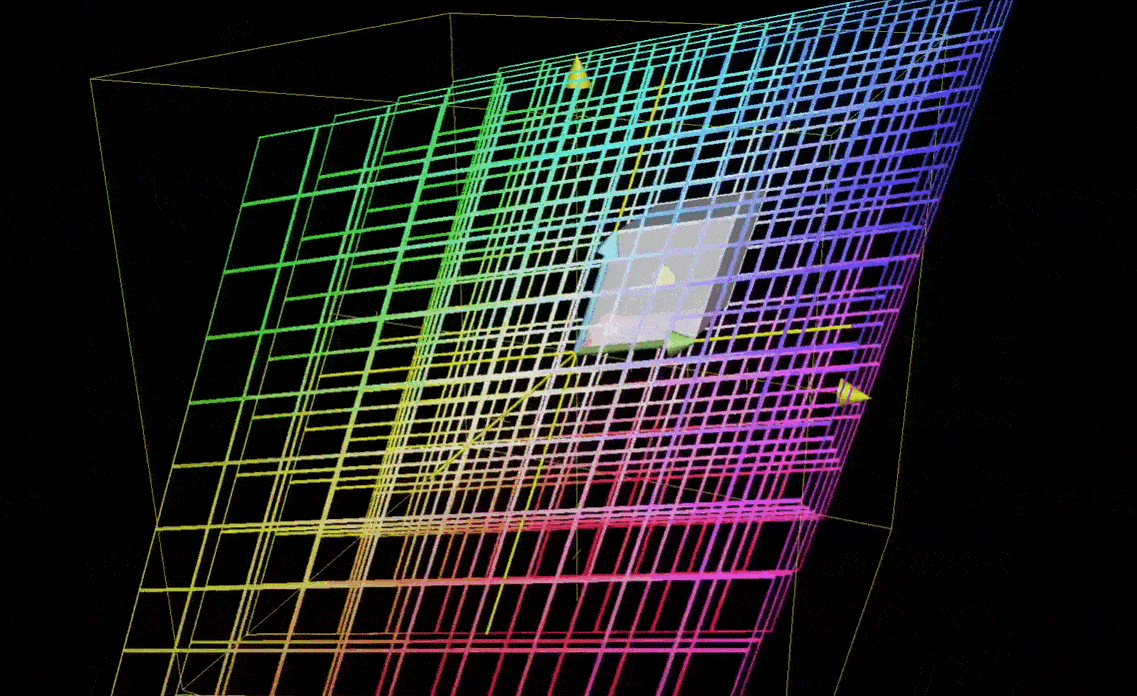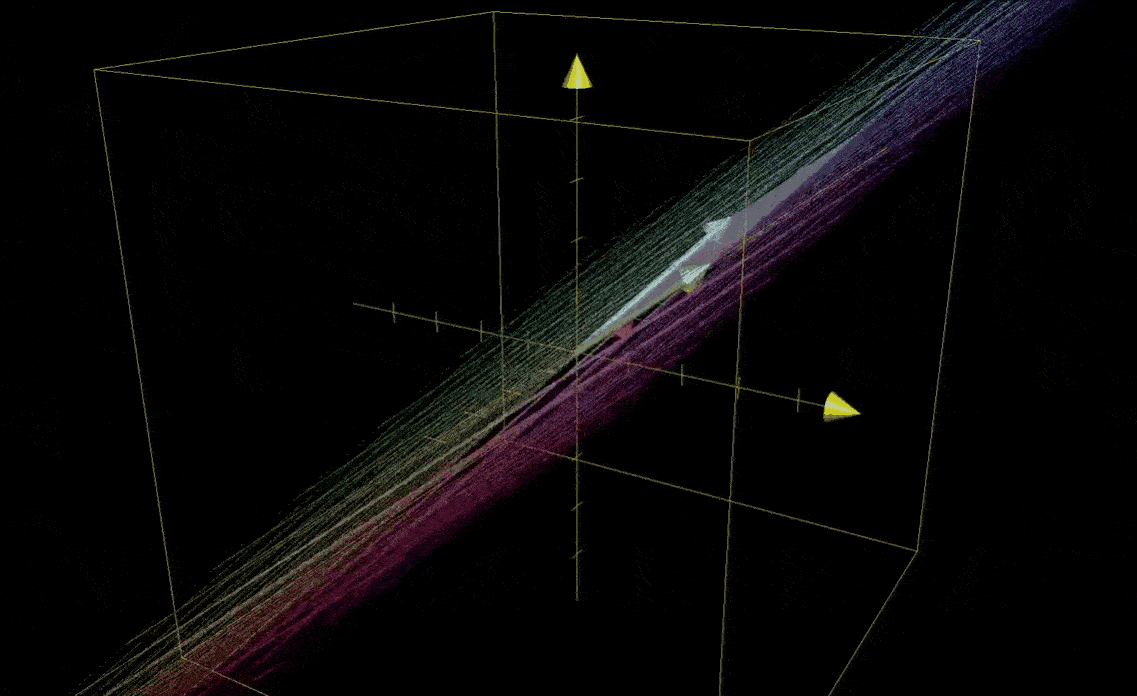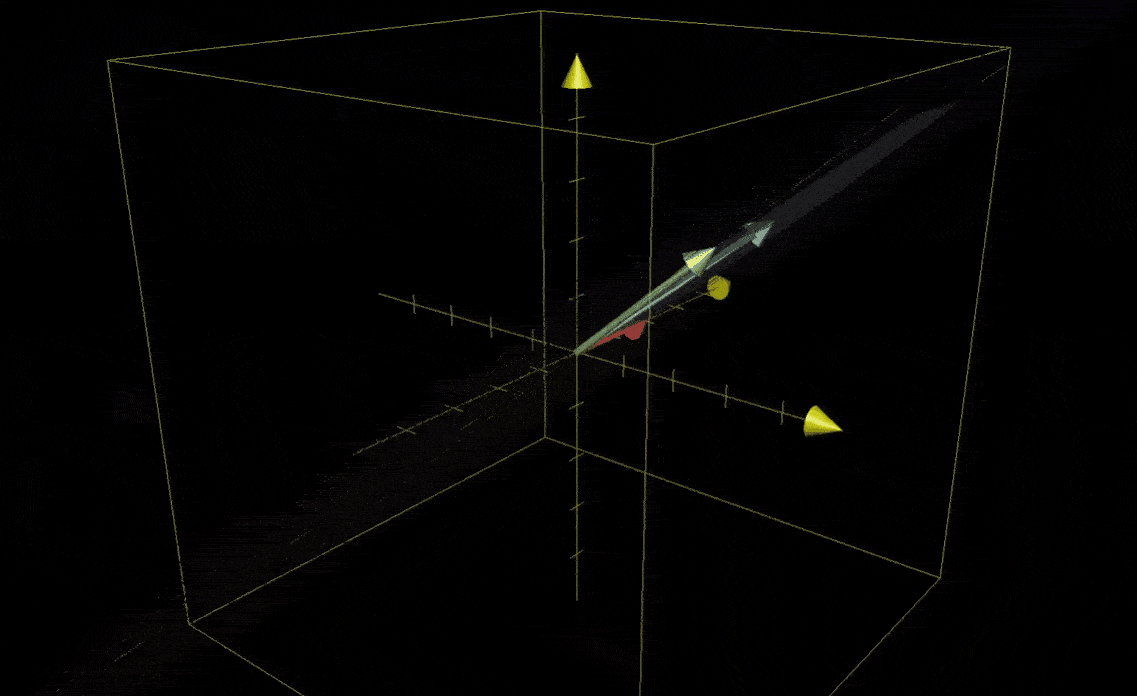
行列式为0则意味着整个空间被压缩为零体积的东西,也就是一个平面或一条直线,或者更极端的情况下,一个点,这意味着,矩阵的列必然线性相关
-
那么对于负值行列式呢?它在三维空间下是什么意思?
-
有一种方法来描述三维空间的定向,那就是 “右手定则” ,右手食指指向i帽的方向,伸出中指指向j帽的方向,当你把大拇指竖起来时,它就正好指向k帽的方向
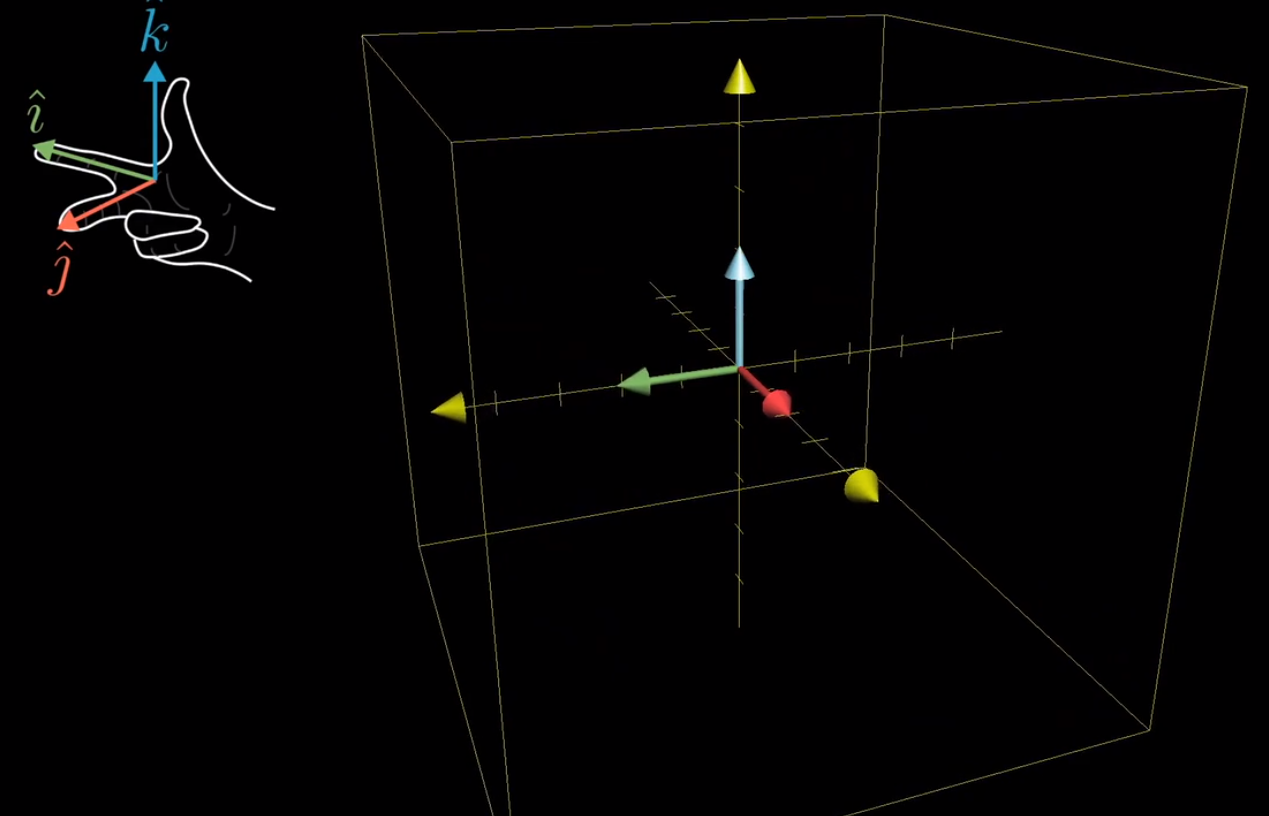
- 如果在变换后你仍然可以这么做,那么定向没有发生改变,行列式为正;否则,如果在变换后你只能用左手这么做,说明定向发生了改变,行列式为负
计算
对于一个 2x2 的矩阵
公式是 $$ ad-bc $$
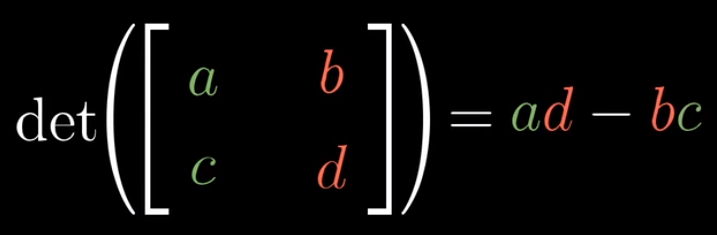
-
以下是对这个公式来源的直观理解,假如b和c均恰好为0,那么a告诉你i帽在x轴方向的伸缩比例,d告诉你j帽在y轴方向的伸缩比例
-
因为其他项均为0,所以ad给出的是单位正方形伸缩后形成的矩形的面积,就像之前[[3,0],[0,2]]那个例子一样,这一点合情合理
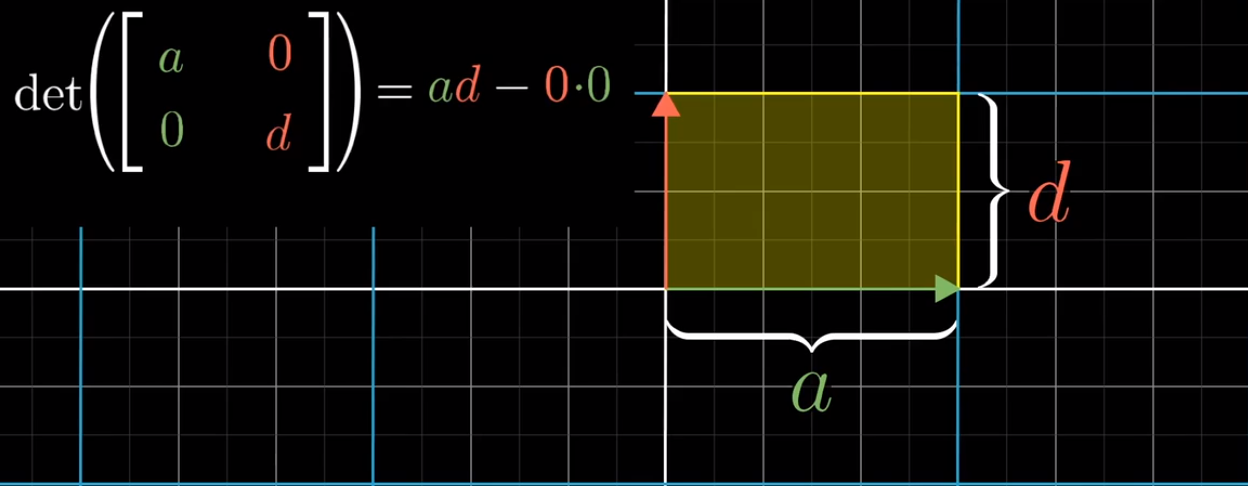
- 即便b和c其中只有一项为0,那么最后得到的是一个平行四边形,底为a且高为d,面积应该仍旧为ad

- 粗略地说,如果b和c均不为0,那么 bc 项就会告诉你平行四边形在对角方向拉伸或压缩了多少
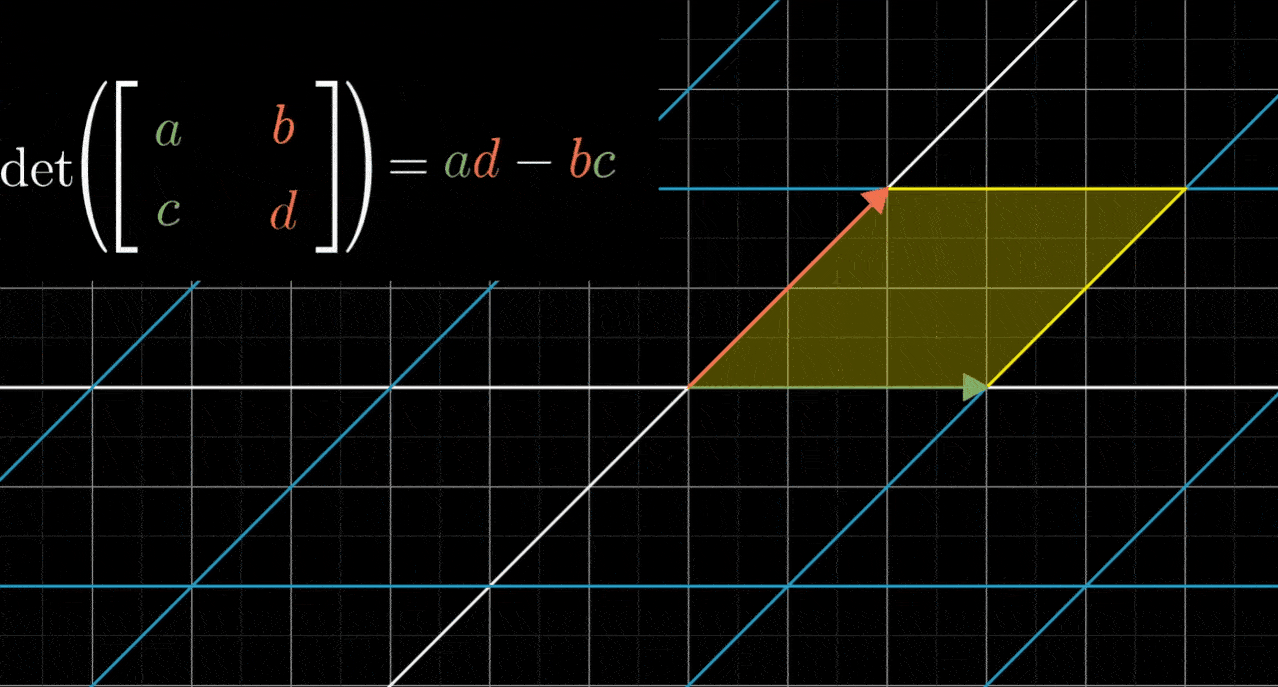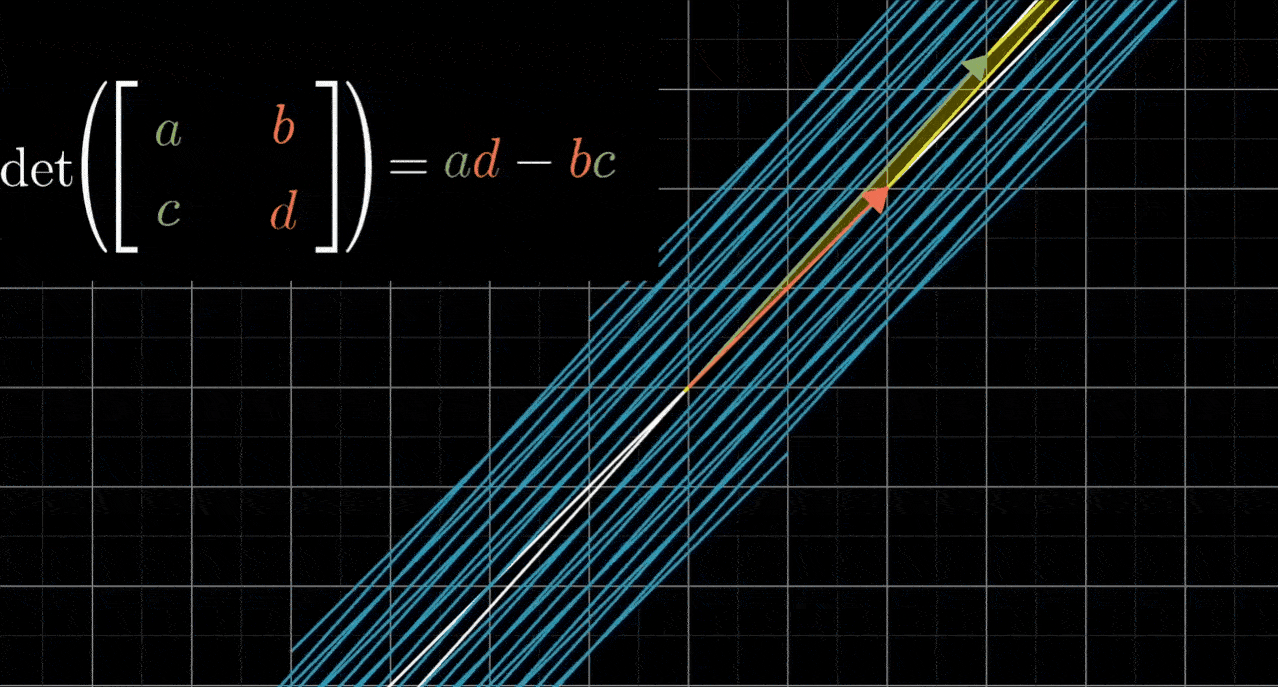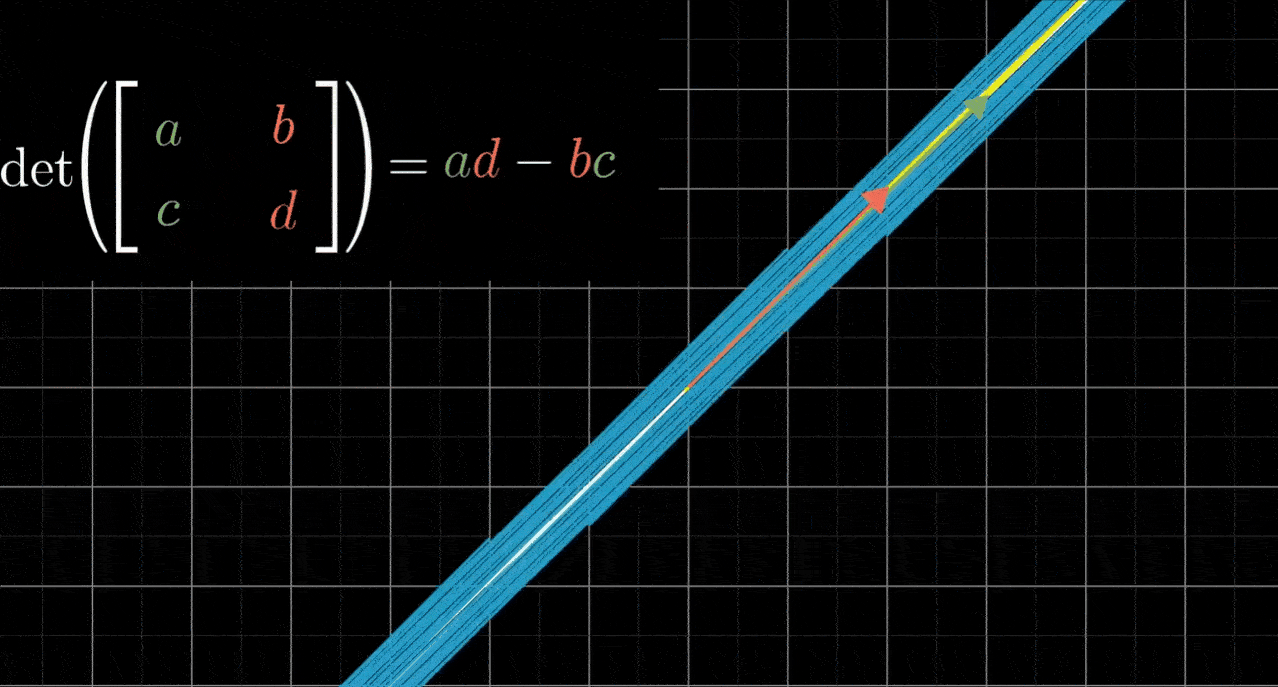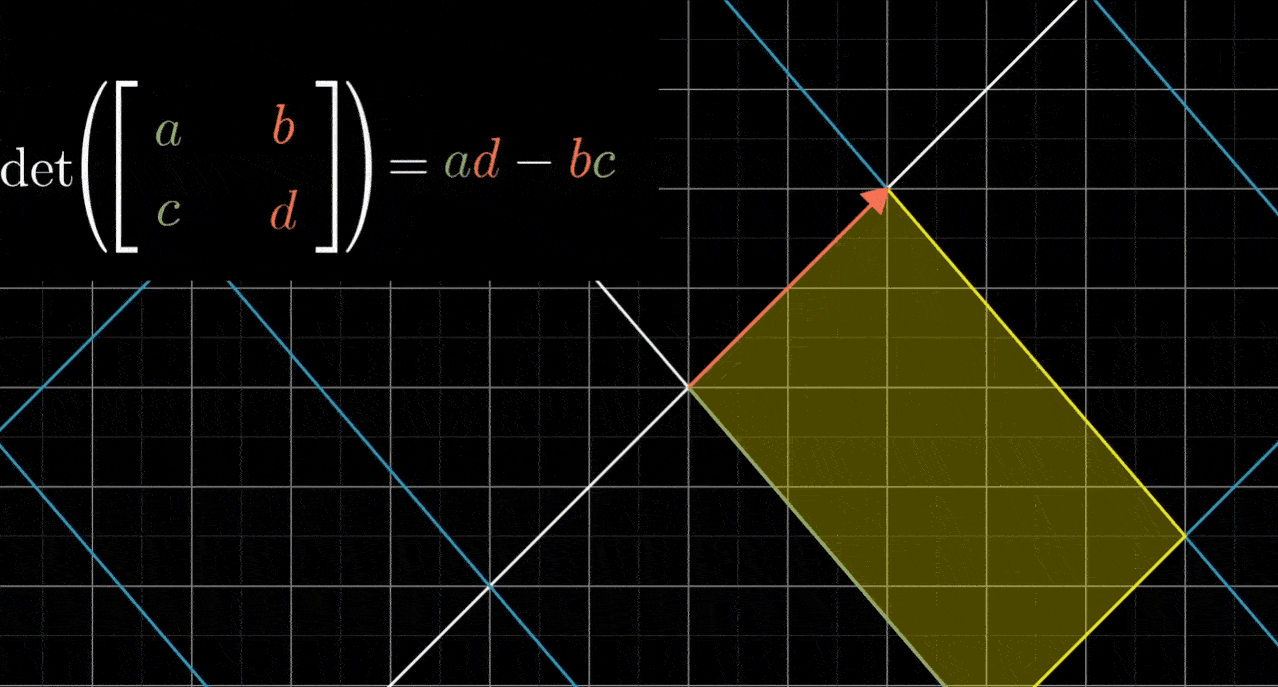
- 对于那些迫切想知道 bc 项精确含义的人,这里有个简图可以帮忙
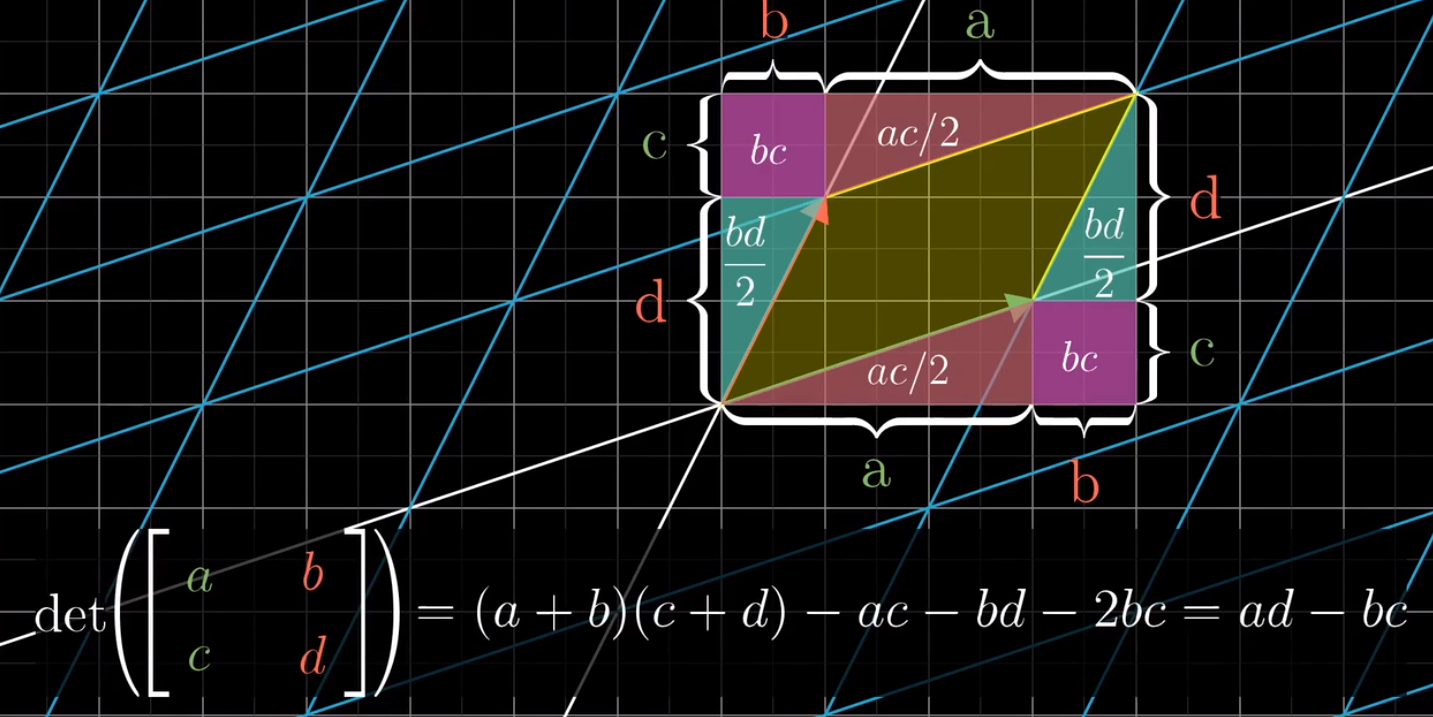
- 顺便给出三阶行列式的计算公式
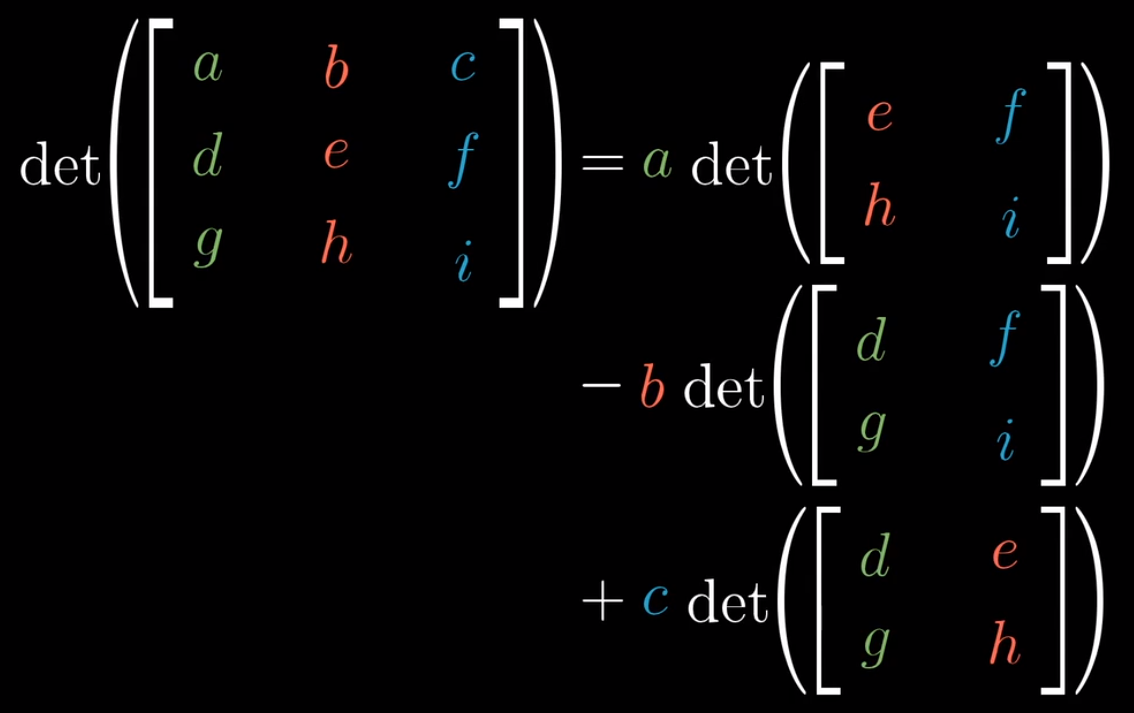
拾遗
- 如果将两个矩阵相乘,它们乘积的行列式,等于这两个矩阵的行列式的乘积