附注1-三维空间中的线性变换

Lisa：呃，我爸爸到底在哪？

Frink：对于能拿到双曲拓补学高等学位的傻瓜来说，

这一点也足够明显——Homer Simpason误入了...（关灯）...三维空间！

三维空间变换

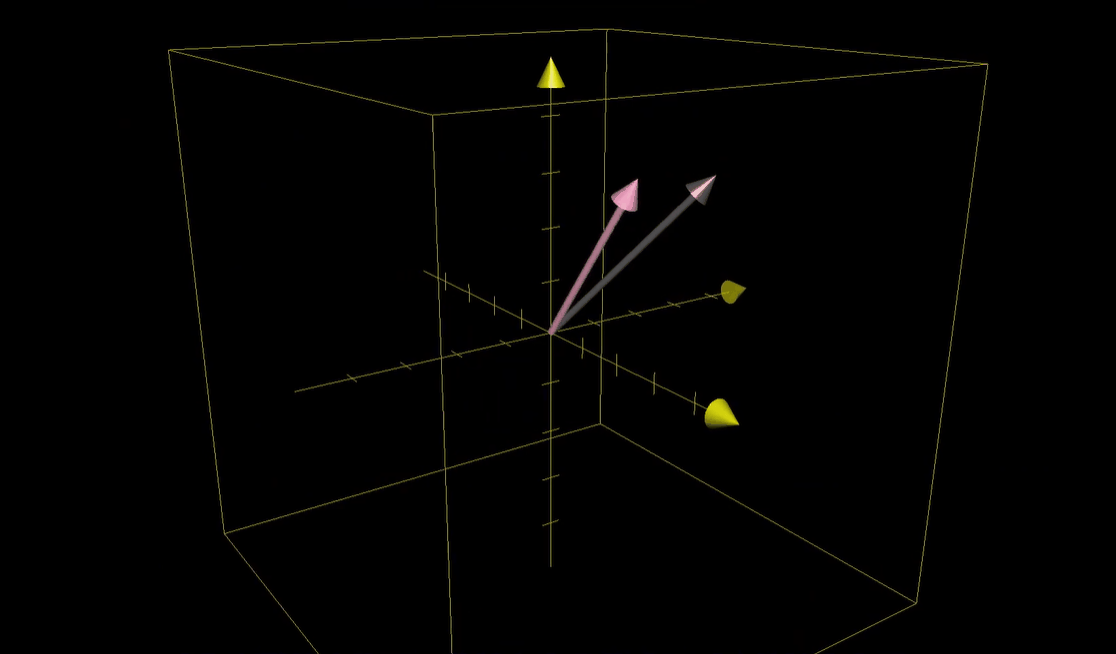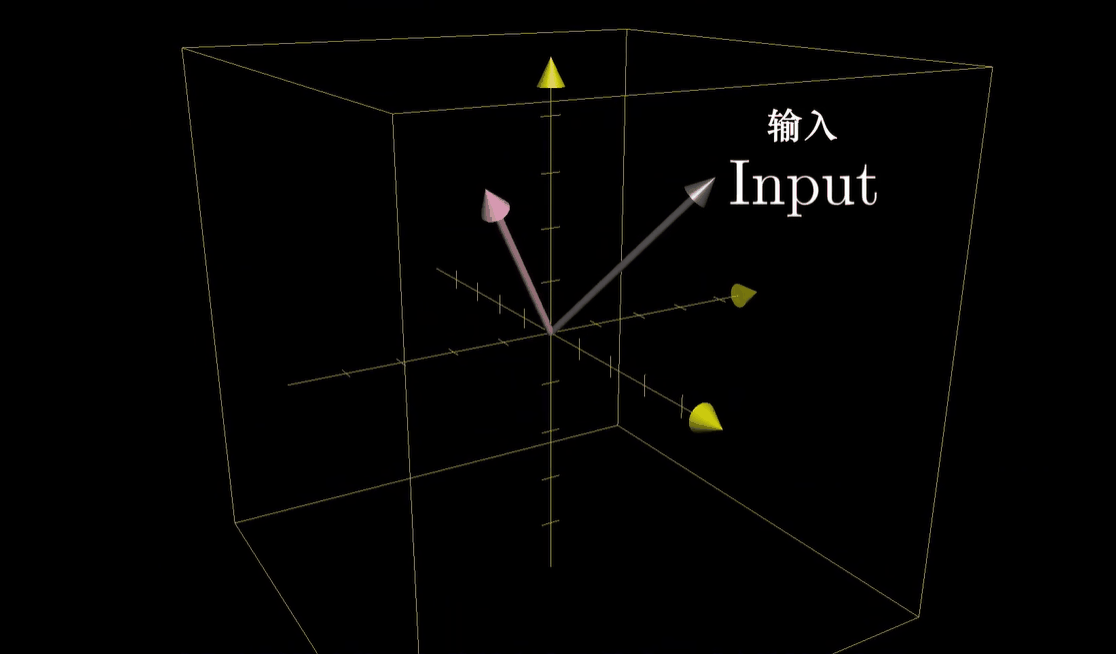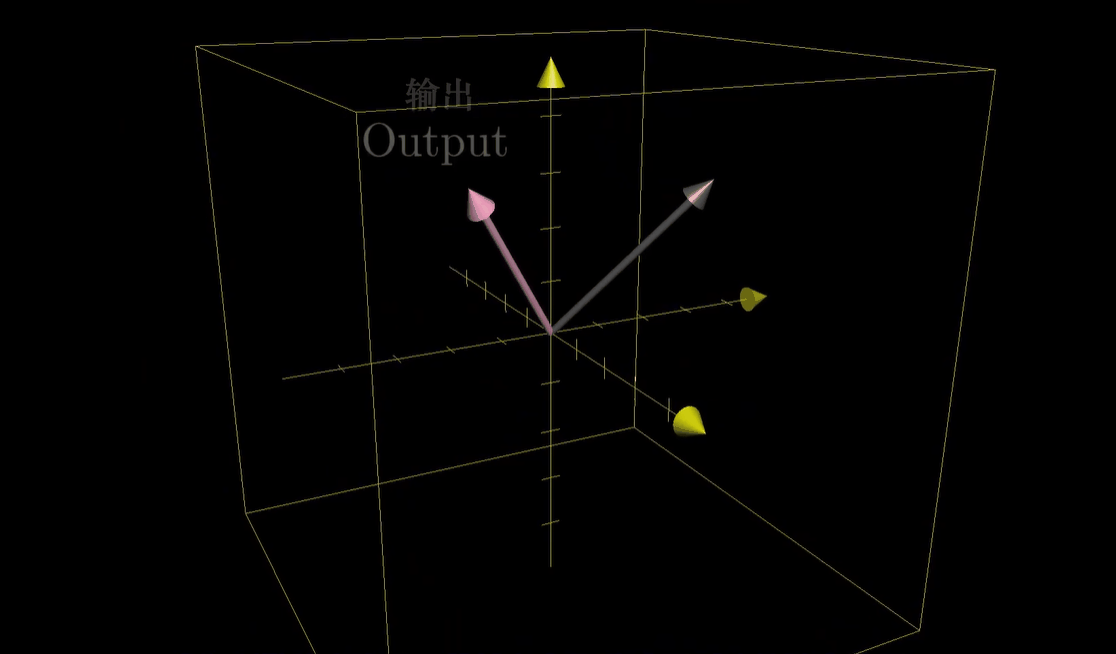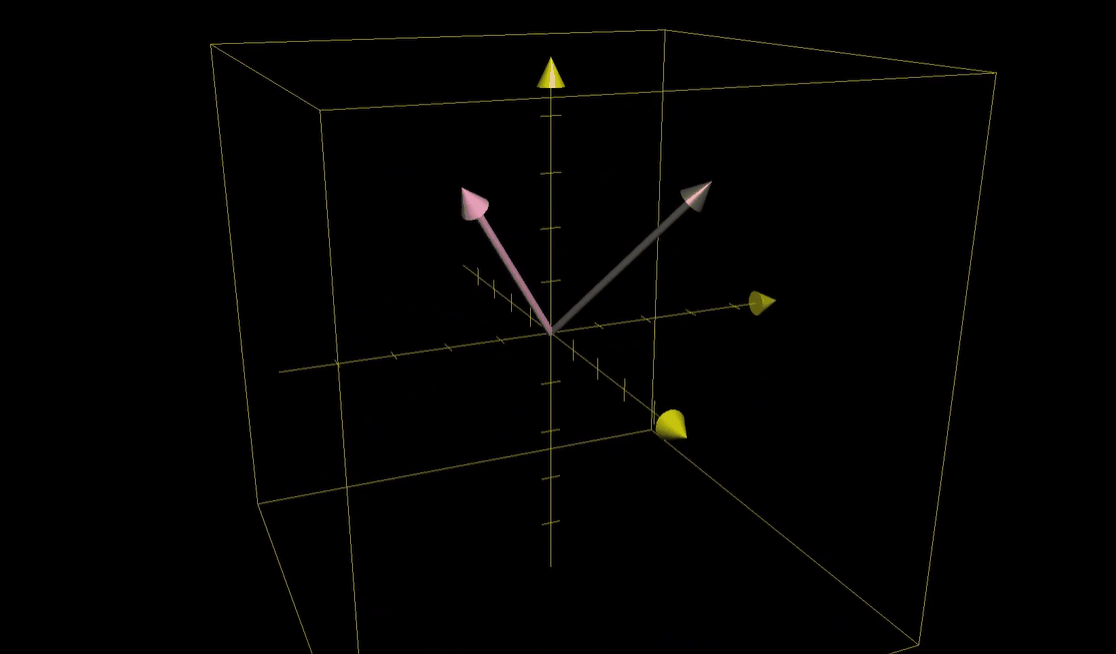
• 比如说，考虑这样一个线性变换，它以三维向量为输入，并以三维向量为输出

• 我们可以想象它在移动三维空间中的所有点（这里用网格表示），保持网格线平行且等距分布，并保持原点不动。和二维情形一样，我们看到的三维空间的每一个点，实际上只是用来代表以它本身为终点的一个向量

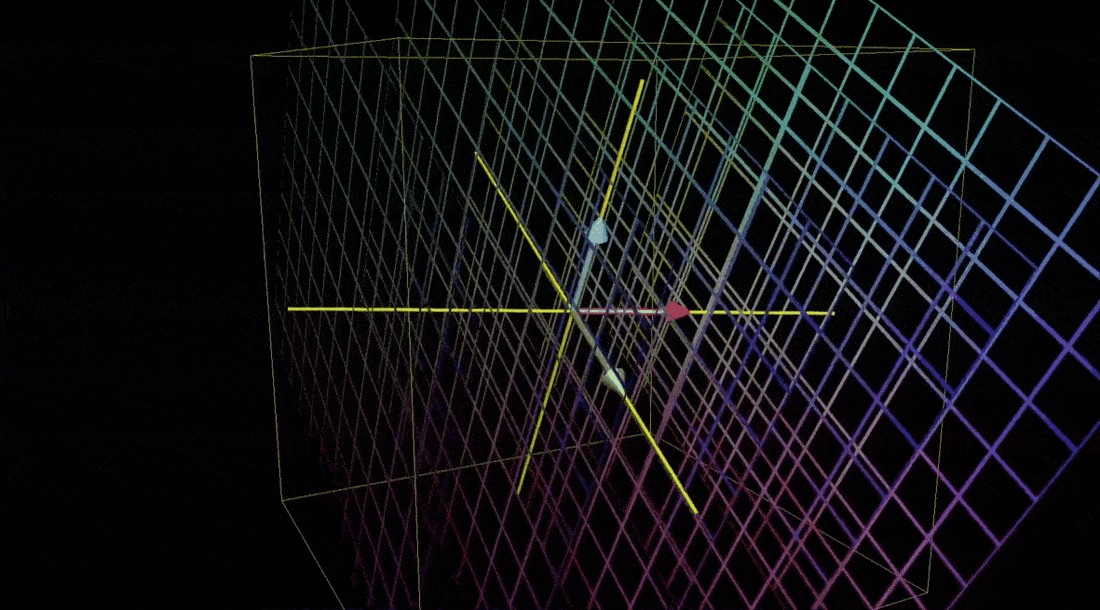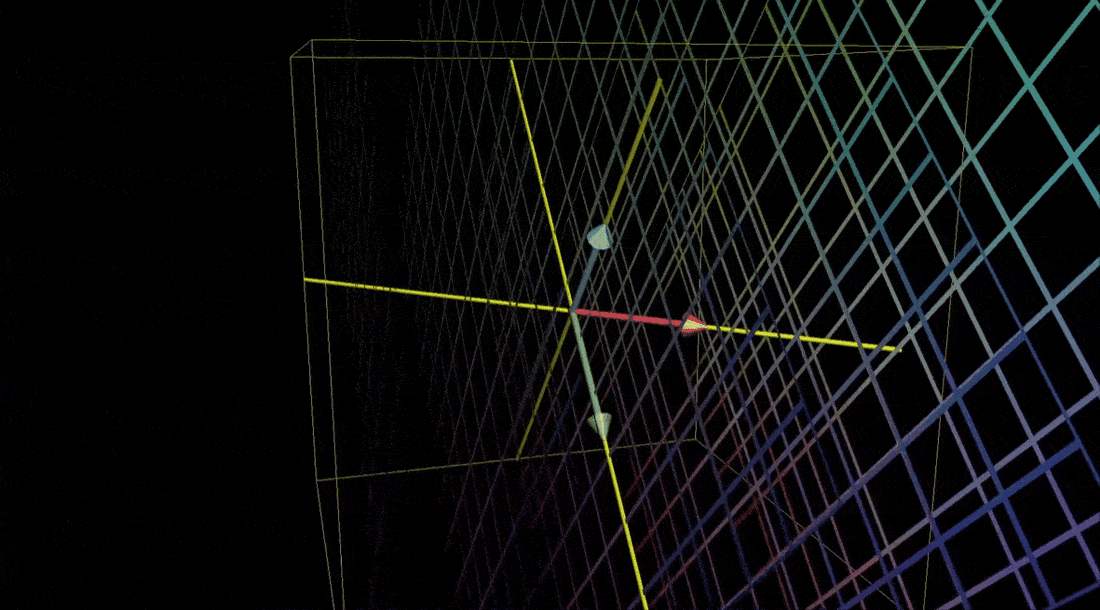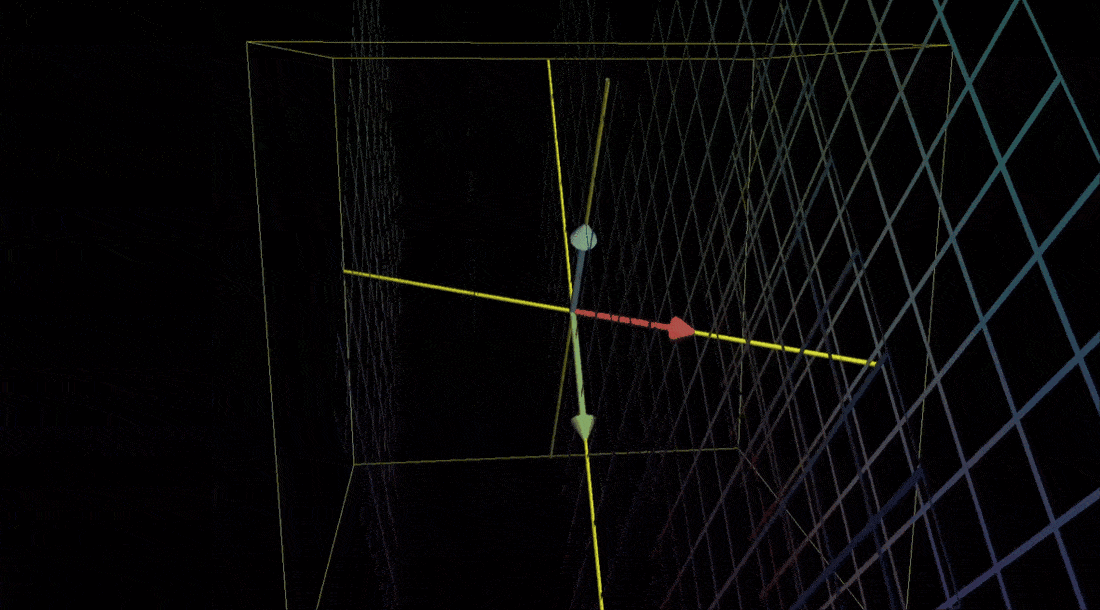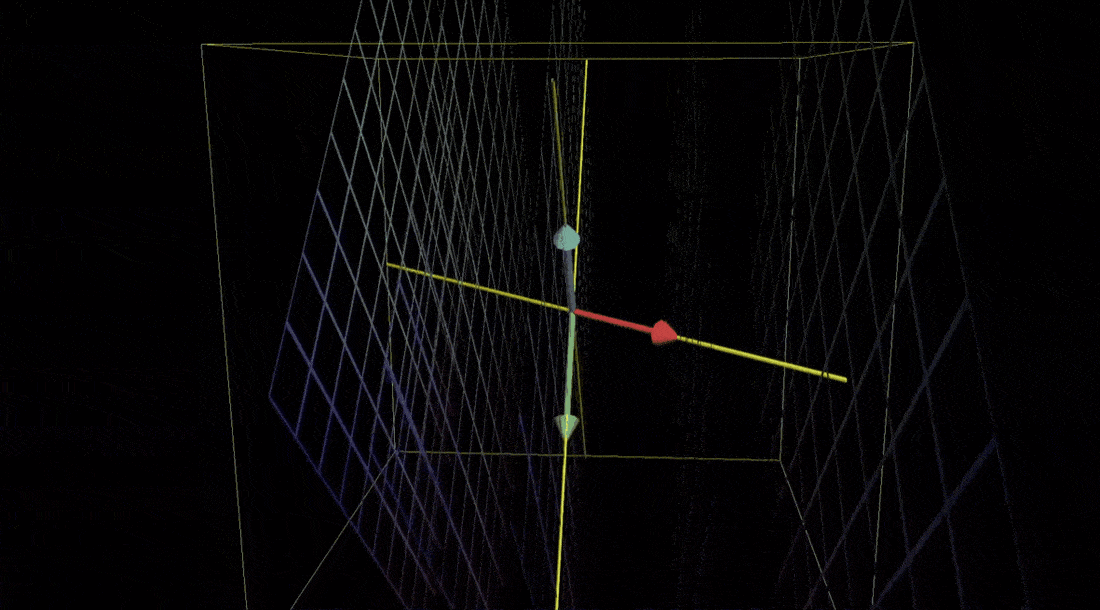
• 而我们所做的变换只是将输入向量移动至对应的输出向量

• 还是和二维情形相同，三维线性变换完全由基向量的去向决定，不过现在我们有三个通常使用的标准基向量

1. x方向的单位向量 “i帽”

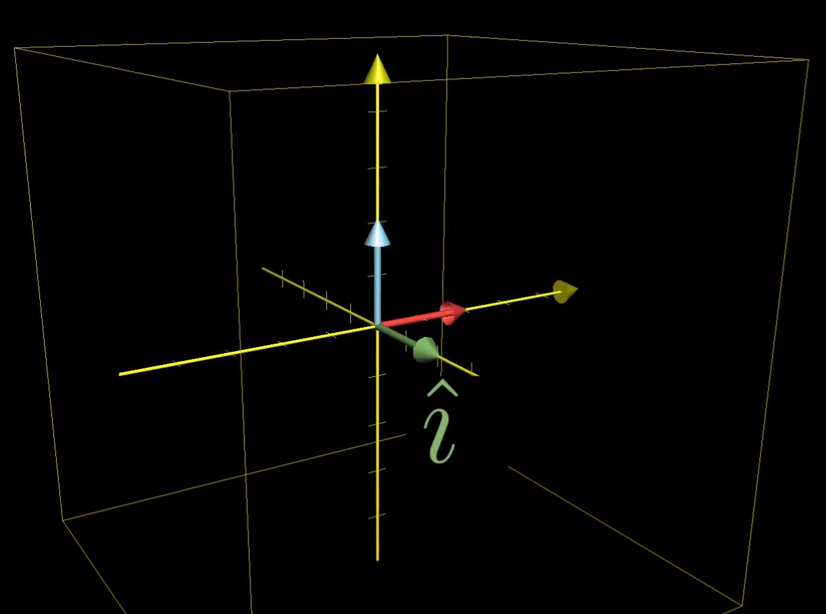
2. y方向的单位向量 “j帽”

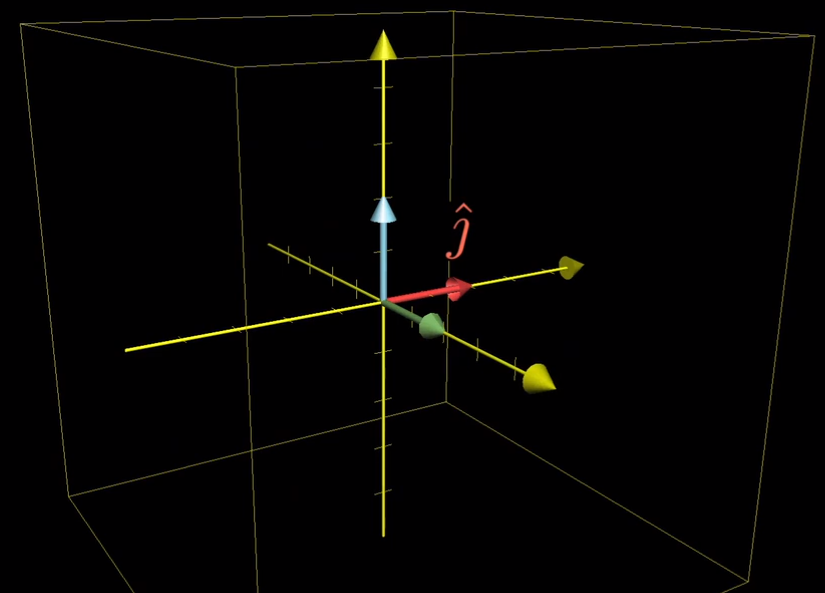
3. 外加一个新来的，z方向的单位向量 “k帽”

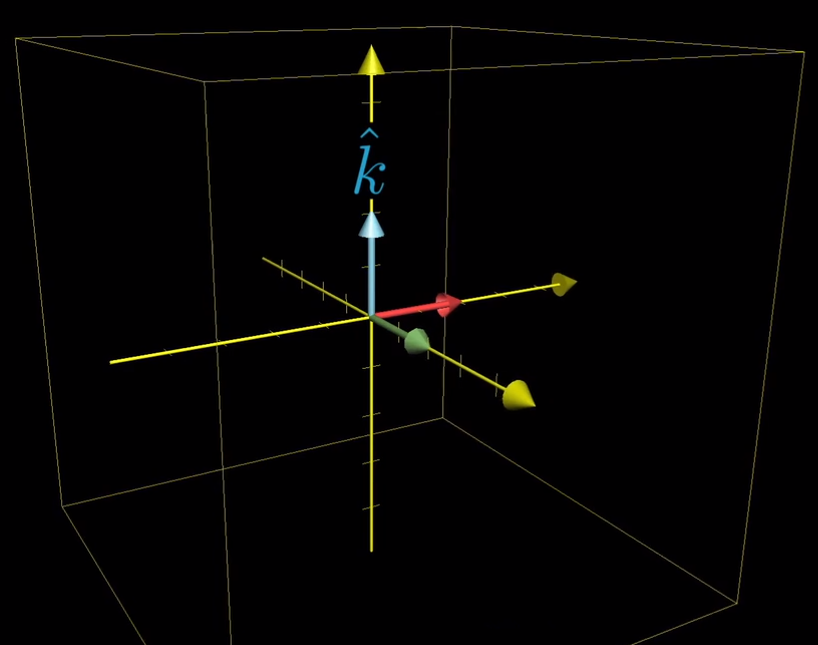
• 实际上，只考虑跟踪这些基向量的话会更容易观察这些线性变换，因为使用三维网格会显得很凌乱
• 在背景中留下原始坐标轴的副本，我们就能观察到三个基向量变换后的位置。将变换后三个基向量的坐标记录在一个 3x3 的矩阵中，仅仅使用九个数字，这个矩阵就完全描述了一个线性变换

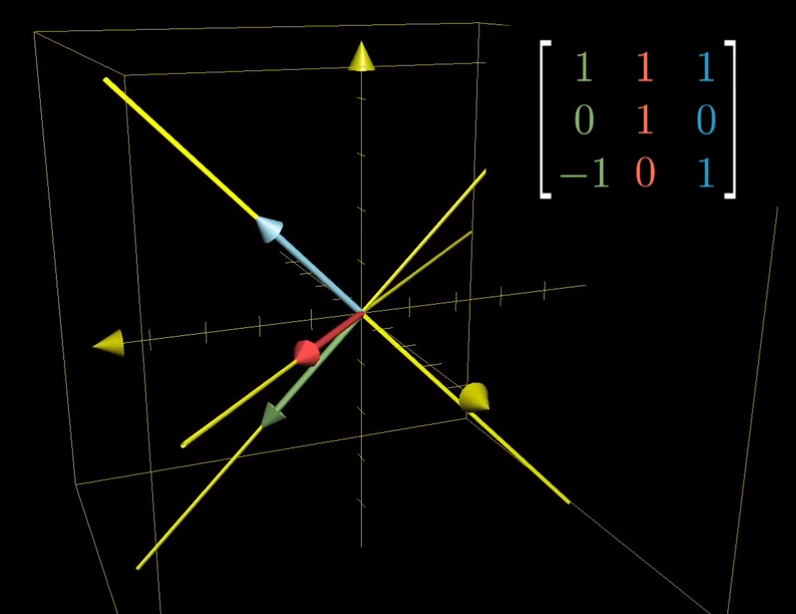
• 举个简单的例子，考虑沿着y轴旋转90度的变换

• 这个变换将i帽移动到z轴上的（0，0，-1）；它不移动j帽，所以j帽仍旧在（0，1，0）；而k帽被移动至x轴上的（1，0，0），这三组坐标就成为了描述这一旋转变换的矩阵的三列

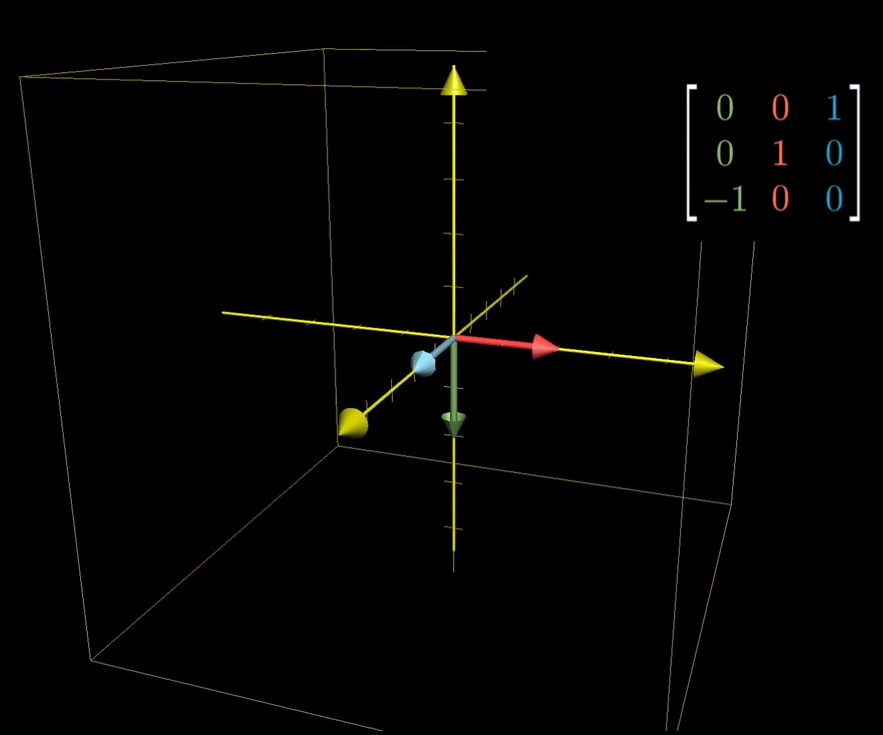
• 要想知道（x，y，z）所代表的向量在变换后的去向，推理过程与在二维空间下几乎相同

• 它的每个坐标都可以看作对相应基向量的缩放，从而使缩放结果的和为你选择的向量

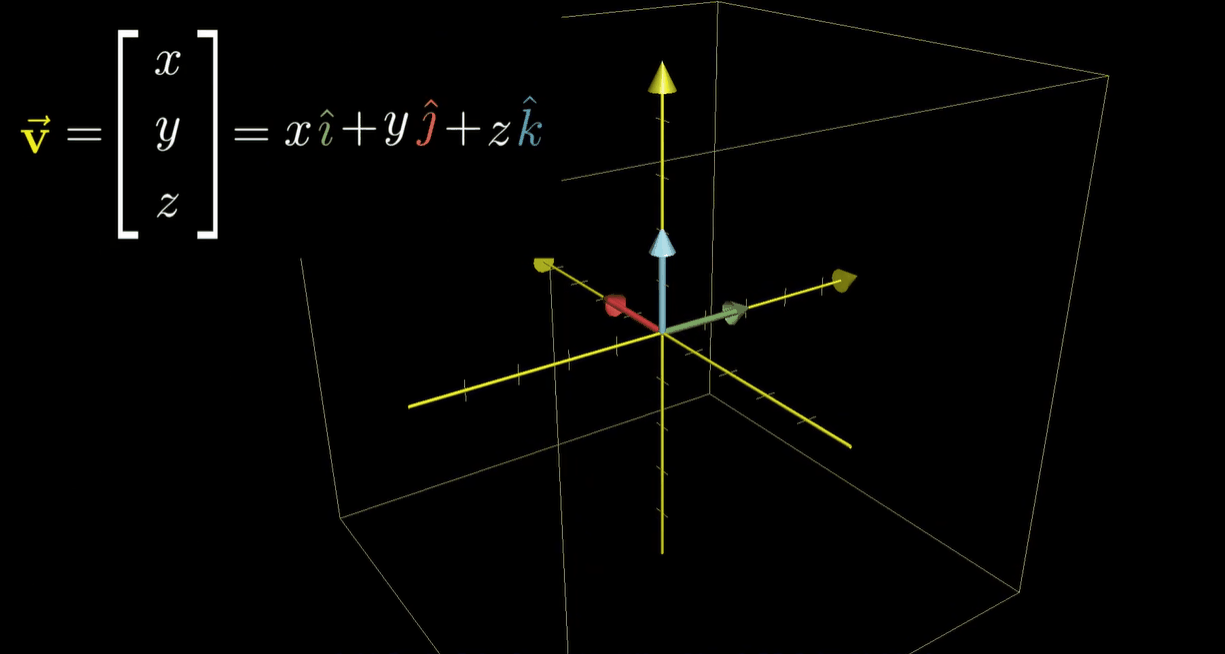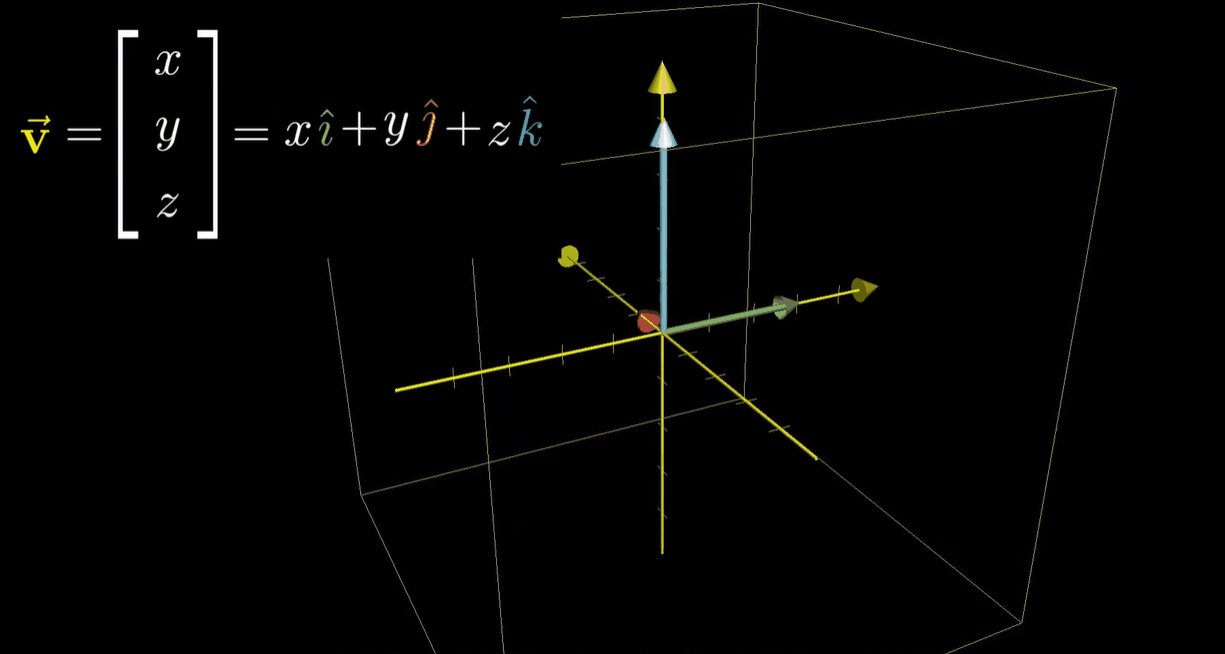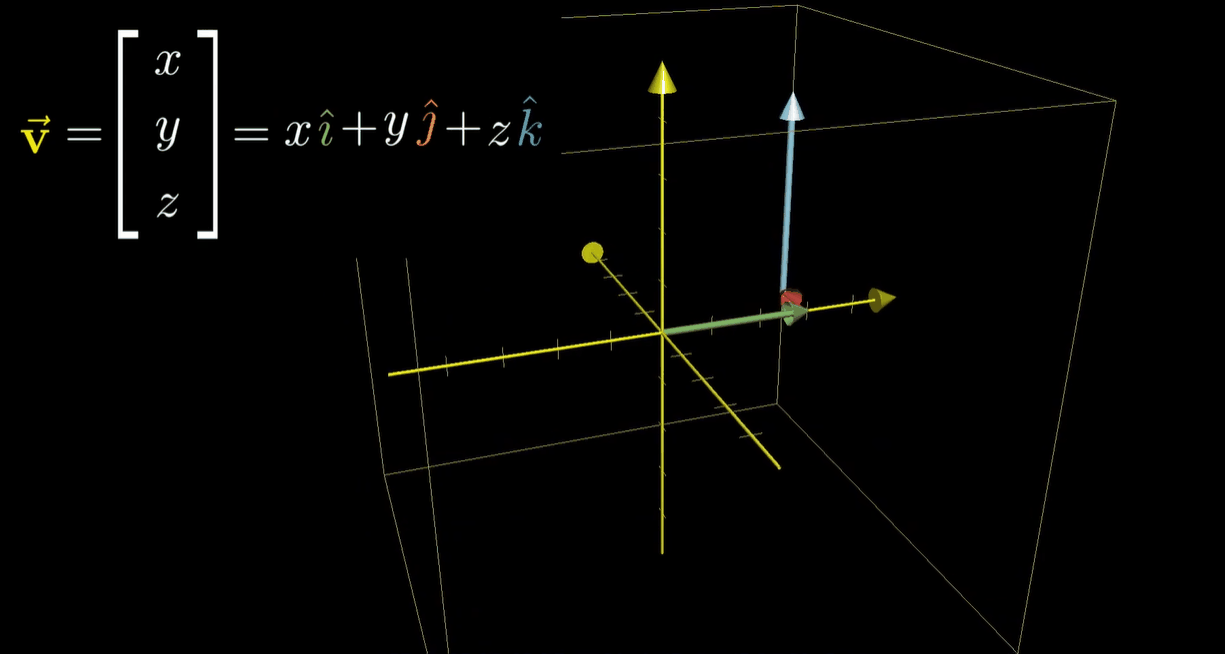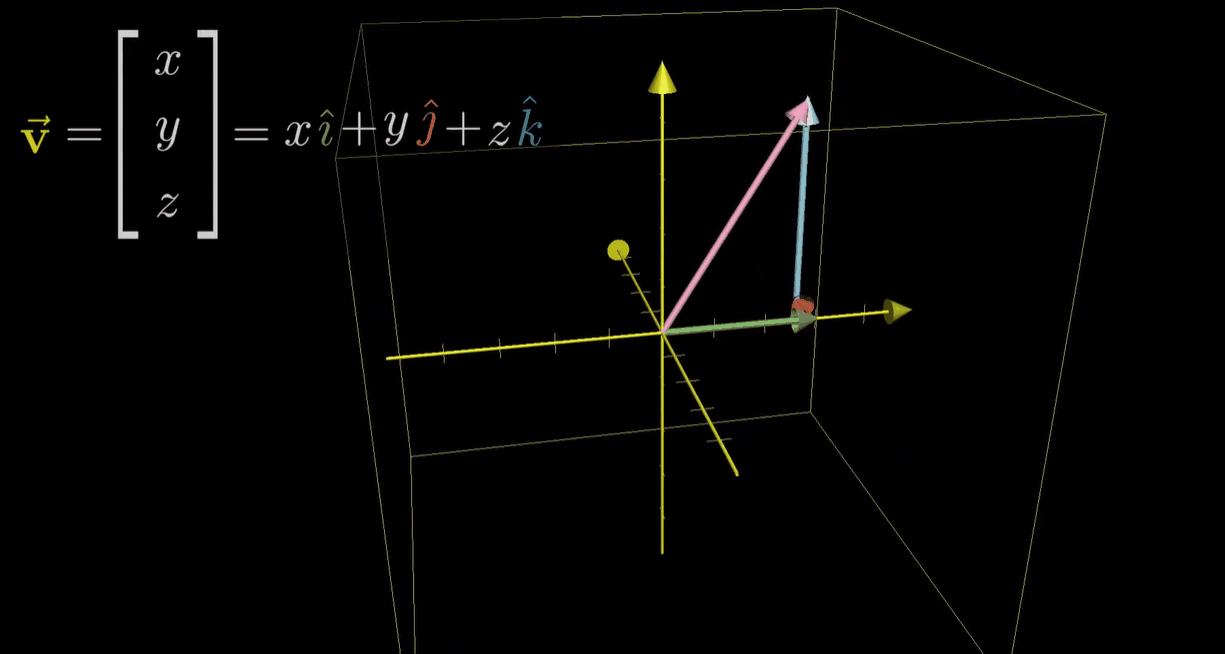
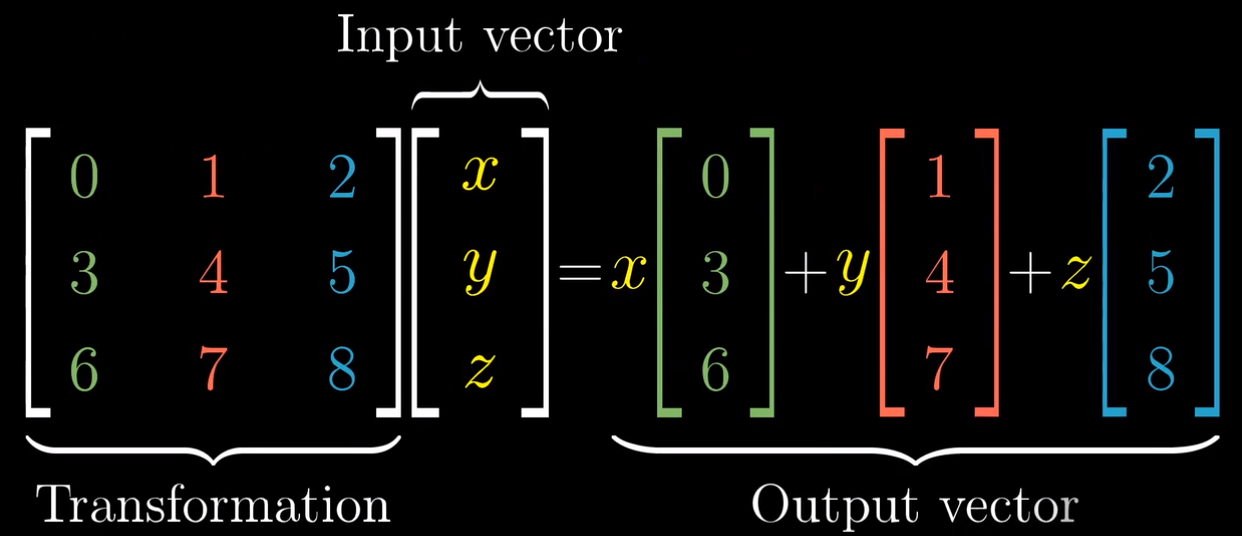
• 和二维类似，重要的部分在于，这一 “缩放再相加” 的过程在变换前后均适用。所以要找到向量变换后的位置，将它的坐标与矩阵的对应列相乘，再将结果相加即可

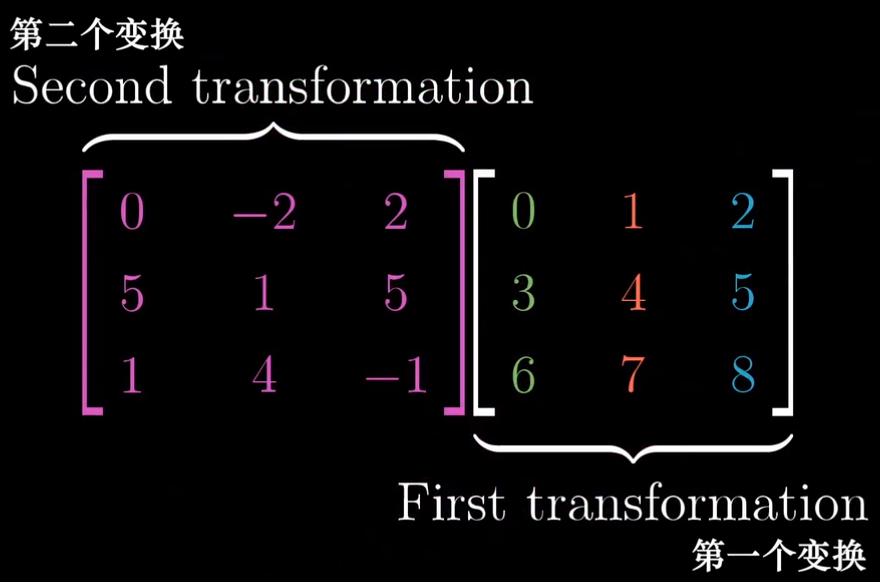
• 两个矩阵相乘也是类似的，当看到两个 3x3 矩阵相乘时，应该想象首先应用右侧矩阵代表的变换，然后应用左侧矩阵代表的变换

• 虽然三维空间中的旋转很难直接表述，但是如果将它分解为简单分立的旋转的复合，这一过程就很容易理解了

• 三维下通过数值计算矩阵乘法依旧与二维情形类似

时刻记住 ”两个线性变换依次作用“ 这一想法